Содержание
- 2. АППРОКСИМАЦИЯ Найти φ(х)=?, такую что φ(xi)≈yi
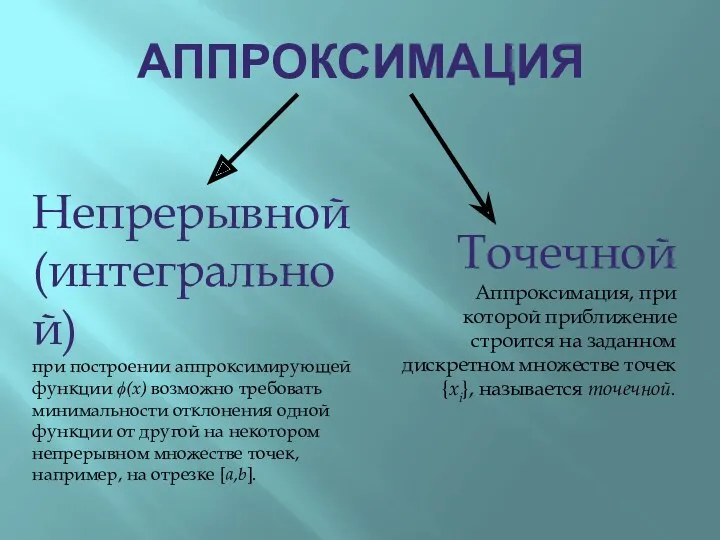
- 3. АППРОКСИМАЦИЯ Непрерывной (интегральной) при построении аппроксимирующей функции ϕ(x) возможно требовать минимальности отклонения одной функции от другой
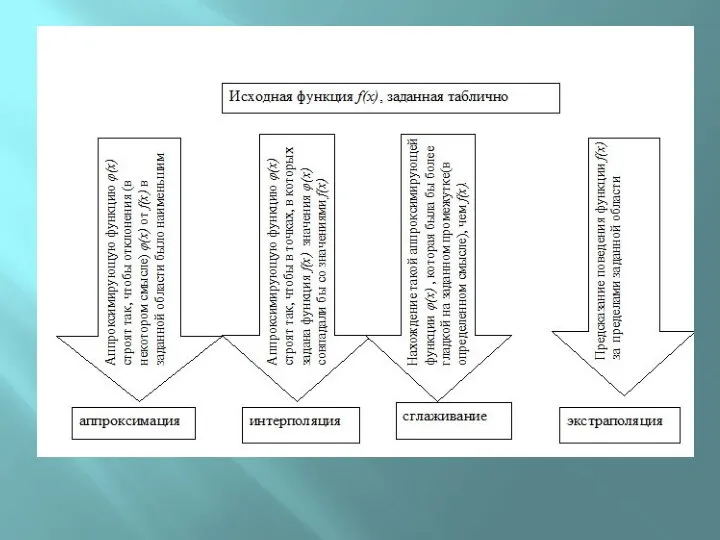
- 6. Пусть функция у= f(x). задана таблицей значений Аппроксимирующую функцию ϕ(x) будем строить таким образом, чтобы ее
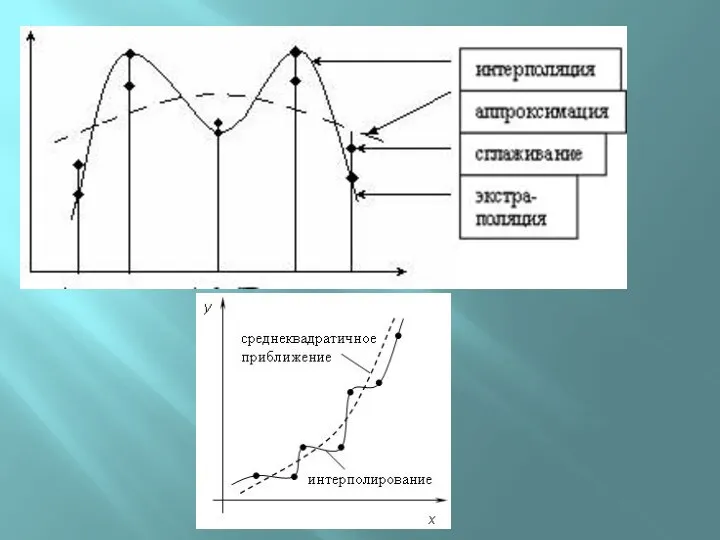
- 7. ИНТЕРПОЛЯЦИЯ Глобальной - если на всем интервале интерполяции [x0, xn], содержащем n+1 узлов, строят один полином
- 8. Интерполяция степенным многочленом (полиномом). Через точек на плоскости можно провести кривую, являющуюся графиком степенного многочлена (полинома)
- 9. Определитель матрицы, известный в алгебре как определитель Вандермонда, если среди узлов xi нет совпадающих :
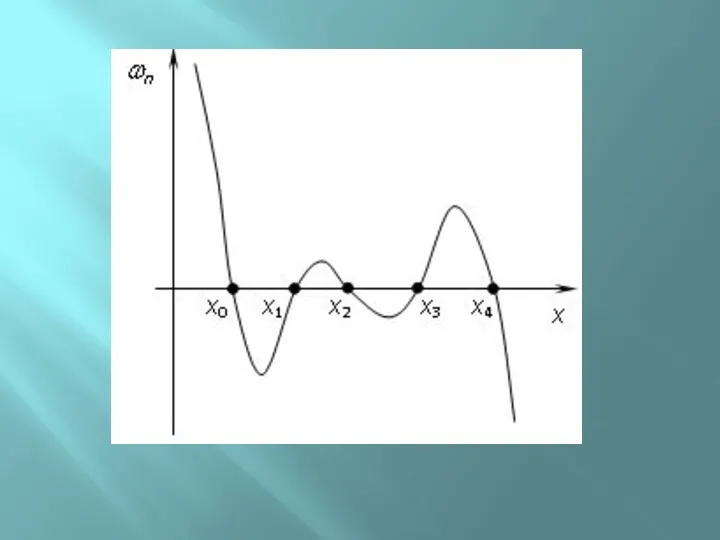
- 10. Погрешность глобальной интерполяции
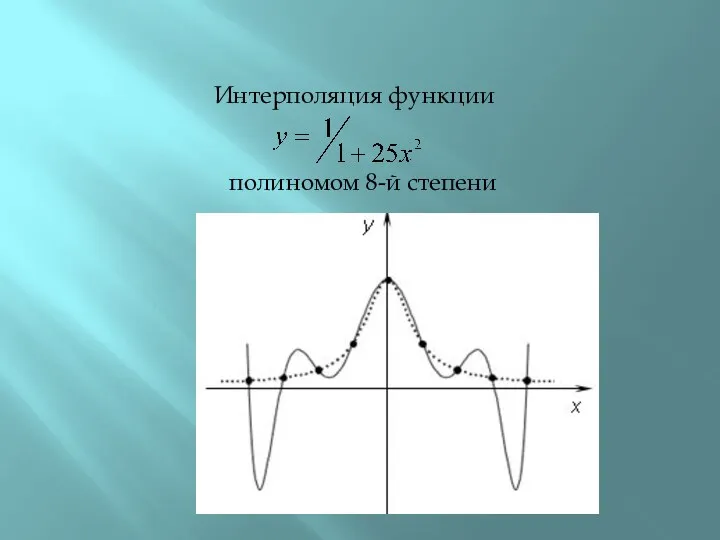
- 12. Интерполяция функции полиномом 8-й степени
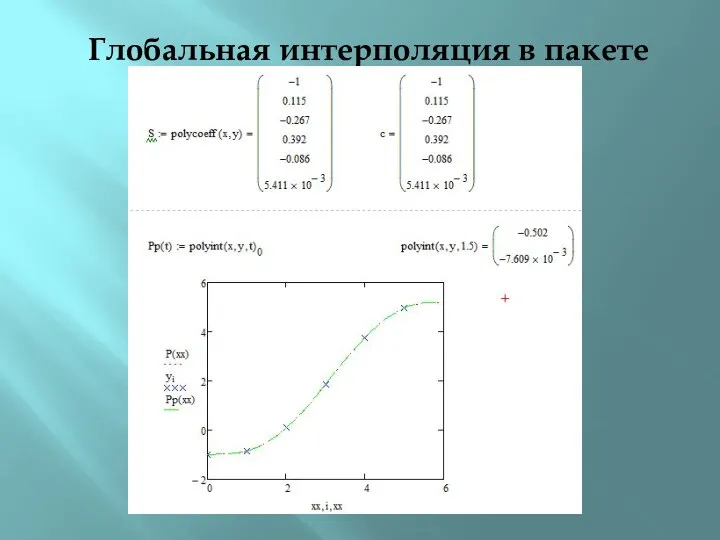
- 13. Глобальная интерполяция в пакете Mathcad
- 14. Глобальная интерполяция в пакете Mathcad
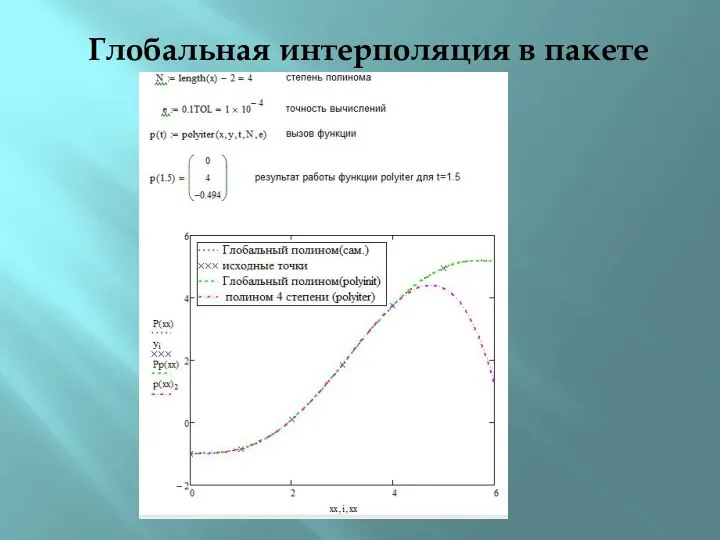
- 15. Глобальная интерполяция в пакете Mathcad
- 16. ЛОКАЛЬНАЯ ИНТЕРПОЛЯЦИЯ Кусочно-линейная Сплайн-интерполяция.
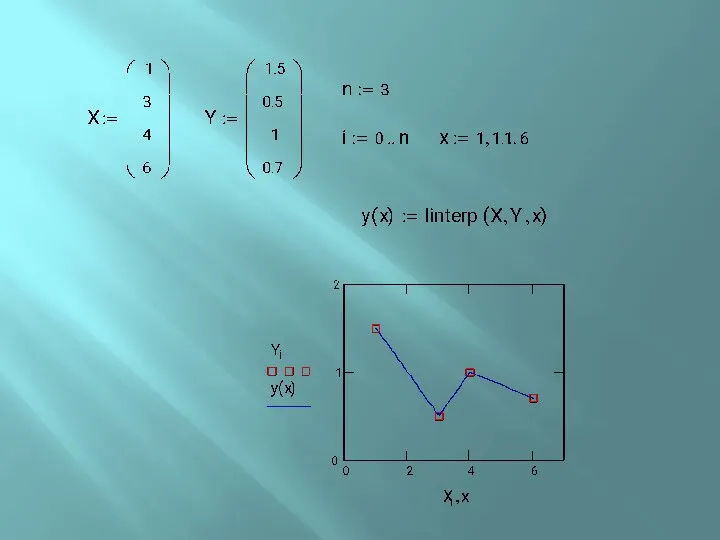
- 17. Кусочно-линейная интерполяция Осуществляет кусочно-линейную интерполяцию функция linterp(vx, vy, x). vx и vy, векторая, содержащие исходные данные
- 19. Сплайн-интерполяция. Сплайн – это функция, которая на каждом частичном интервале представляется полиномом некоторой степени, и на
- 20. Кубический сплайн Условия для определения коэффициентов вытекают из так называемых условий сшивания соседних сплайнов в узловых
- 21. Физико-механическое обоснование интерполяция сплайнами . При совмещении упругой металлической линейки с узловыми точками, форма, которую примет
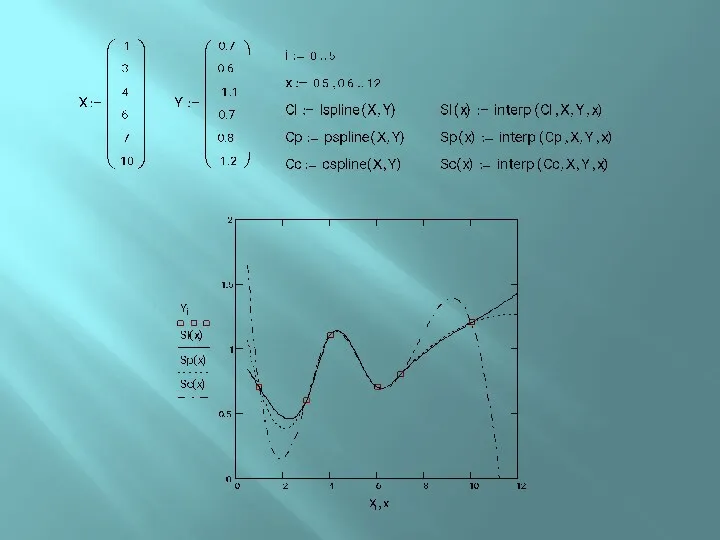
- 22. Функции кубической сплайн-интерполяции. lspline(vx, vy) pspline(vx, vy) cspline(vx, vy) функции, возвращающие коэффициенты сплайнов; interp(vs, vx, vy,
- 23. Функции кубической сплайн-интерполяции. lspline генерирует кривую сплайна, которая приближается к прямой линии в граничных точках; pspline
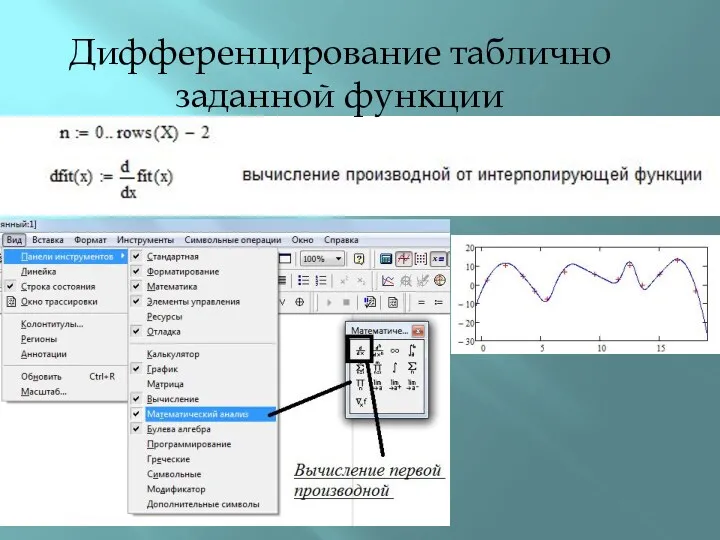
- 25. Дифференцирование таблично заданной функции
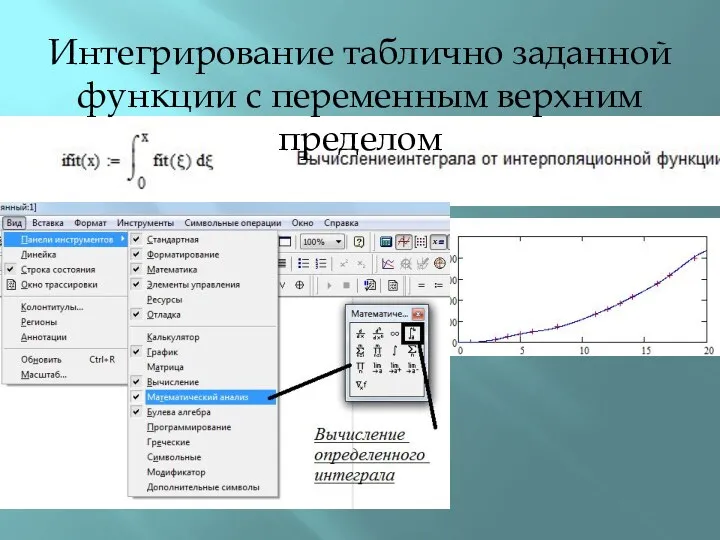
- 26. Интегрирование таблично заданной функции с переменным верхним пределом
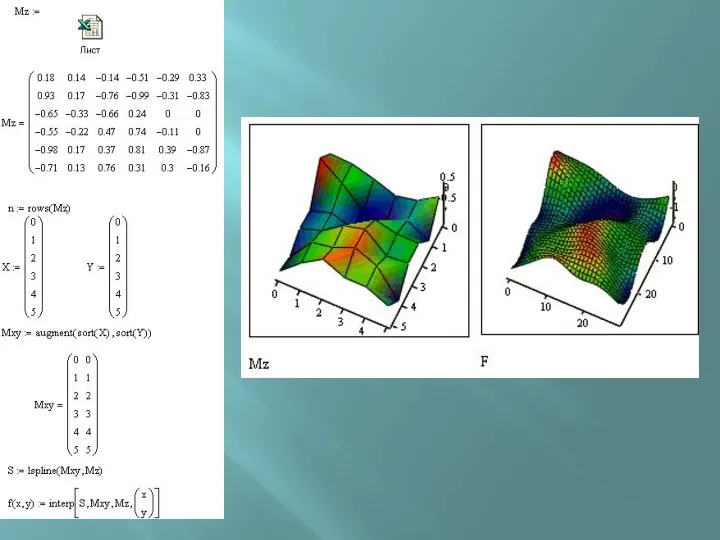
- 27. Функции двух переменных В пакете Mathcad существуют встроенные функции для интерполяции функции двух переменных. Эти функции
- 29. Экстраполяция функций. В Mathcad имеется функция для проведения экстраполяции, которая учитывает распределение данных вдоль всего интервала:
- 30. Значений аргумента для данных не требуется, поскольку по определению функция действует на данные, идущие друг за
- 32. Скачать презентацию


![ИНТЕРПОЛЯЦИЯ Глобальной - если на всем интервале интерполяции [x0, xn],](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/410973/slide-6.jpg)













 Презентация : Использование логических блоков Дьенеша в процессе развития математических представлений дошкольников
Презентация : Использование логических блоков Дьенеша в процессе развития математических представлений дошкольников Средние величины
Средние величины Жай бөлшектер мен аралас сандарды салыстыру
Жай бөлшектер мен аралас сандарды салыстыру Змінні
Змінні Площади фигур. Обобщающее повторение. 8 класс
Площади фигур. Обобщающее повторение. 8 класс Сравнение чисел
Сравнение чисел Площадь криволинейной трапеции
Площадь криволинейной трапеции График линейного уравнения с двумя переменными
График линейного уравнения с двумя переменными Путешествие в страну треугольников
Путешествие в страну треугольников Эталоны и их классификация. (Лекция 3)
Эталоны и их классификация. (Лекция 3) Приближенные значения чисел. Округление чисел
Приближенные значения чисел. Округление чисел Уравнения и неравенства с двумя переменными
Уравнения и неравенства с двумя переменными Полярные координаты. Параметрическая форма кривых
Полярные координаты. Параметрическая форма кривых Теорема синусов и косинусов
Теорема синусов и косинусов Математика в рабочих профессиях
Математика в рабочих профессиях Теорема Пифагора
Теорема Пифагора Математический зоопарк
Математический зоопарк Конкретный смысл действия умножения
Конкретный смысл действия умножения Письмове ділення на одноцифрове число. Знаходження частини числа. Задачі на знаходження частини числа
Письмове ділення на одноцифрове число. Знаходження частини числа. Задачі на знаходження частини числа Кубизм в архитектуре. Оригами
Кубизм в архитектуре. Оригами Скорость. Время. Расстояние
Скорость. Время. Расстояние Прямоугольный параллелепипед
Прямоугольный параллелепипед Решение задач и выражений. Закрепление вычислительных навыков
Решение задач и выражений. Закрепление вычислительных навыков ОГЭ. Математика. Задания 1-5. Демо-версия
ОГЭ. Математика. Задания 1-5. Демо-версия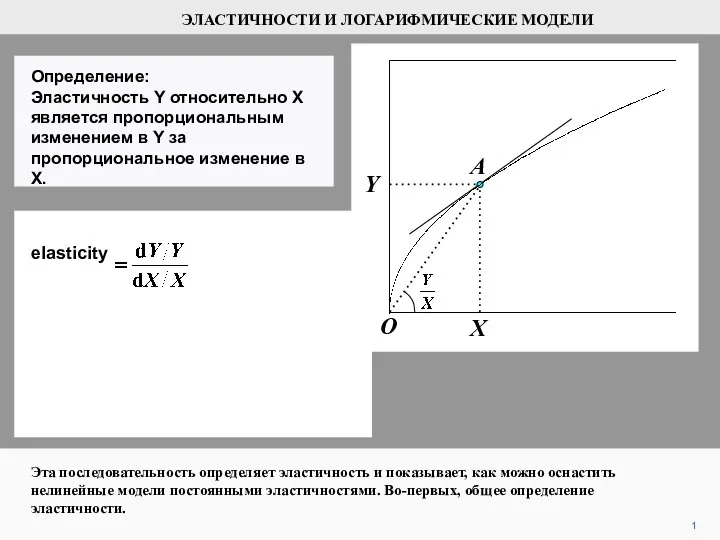 Эластичности и логарифмические модели
Эластичности и логарифмические модели Теория измерений. (Модуль 2)
Теория измерений. (Модуль 2) Сколько в пуде, соли. Познавательное чтение
Сколько в пуде, соли. Познавательное чтение Показательная функция, ее свойства и график
Показательная функция, ее свойства и график