Содержание
- 2. Способы задания последовательности: 1. Словесный. Пример: последовательность четных чисел. 2. Аналитический (задана формула n – го
- 4. Свойства числовых последовательностей. 1°. Ограниченность сверху. Последовательность (уn) ограниченна сверху, если существует такое число М, что
- 5. 3°. Возрастание. Последовательность (уn) возрастающая, если каждый её член(кроме первого) больше предыдущего. 4°. Убывание. Последовательность (уn)
- 7. Определение. Число b называют пределом последовательности (уn), если в любой заранее выбранной окрестности точки b содержатся
- 8. Свойства сходящихся последовательностей. 1. Если последовательность сходится, то только к одному пределу. 1. Если последовательность сходится,
- 10. Предел функции. Предел функции в точке.
- 11. Приращение аргумента. Пусть функция у = f(х) определена в точках х0 и х1. Разность х1 –
- 12. Понятие непрерывности функции. Функция у = f(х) непрерывна в точке х = а, если в этой
- 13. Определение производной. Пусть функция у = f(х) определена в точке х и в некоторой её окрестности.
- 14. Алгоритм нахождения производной для функции у = f(х). Зафиксировать значение х, найти f(х). Дать аргументу х
- 15. Пример нахождения производной функции у = 2х + 3. Фиксируем х=х0, имеем: f(х0 )=2х0 + 3.
- 17. Скачать презентацию














 Моделирование нестационарных течений в газотурбинных двигателях
Моделирование нестационарных течений в газотурбинных двигателях Алгебра логики. Канонические формы логических формул
Алгебра логики. Канонические формы логических формул Действия с десятичными дробями. 8 класс
Действия с десятичными дробями. 8 класс Представление рациональных чисел в виде десятичной дроби (продолжение)
Представление рациональных чисел в виде десятичной дроби (продолжение) Векторная алгебра
Векторная алгебра Научиться выполнять деление с остатком. (3 класс)
Научиться выполнять деление с остатком. (3 класс) Счет предметов, математика, 1 класс
Счет предметов, математика, 1 класс Треугольник и его виды
Треугольник и его виды Сумма углов треугольника
Сумма углов треугольника Решение задач по готовым чертежам (прямоугольный треугольник)
Решение задач по готовым чертежам (прямоугольный треугольник) Ранг матрицы. Метод окаймляющих миноров
Ранг матрицы. Метод окаймляющих миноров Великие ученые математики и их открытия
Великие ученые математики и их открытия Обыкновенные дроби
Обыкновенные дроби Замечательные пределы
Замечательные пределы Элементы комбинаторики
Элементы комбинаторики Математическое моделирование
Математическое моделирование Композиция и макетирование. Закономерности композиции. (Тема 2)
Композиция и макетирование. Закономерности композиции. (Тема 2) Определители. Вычисление определителей высших порядков. Свойства определителей. Алгебраические дополнения и миноры
Определители. Вычисление определителей высших порядков. Свойства определителей. Алгебраические дополнения и миноры Теоремы об углах, образованных двумя параллельными прямыми и секущей. 7 класс
Теоремы об углах, образованных двумя параллельными прямыми и секущей. 7 класс Примеры базовых моделей. Ферментативная кинетика Михаэлиса Ментен. Уравнение Моно. Исследование моделей на устойчивость
Примеры базовых моделей. Ферментативная кинетика Михаэлиса Ментен. Уравнение Моно. Исследование моделей на устойчивость Matrices - Introduction. Lecture 1-3
Matrices - Introduction. Lecture 1-3 Действия с обыкновенными дробями
Действия с обыкновенными дробями Как найти неизвестное вычитаемое
Как найти неизвестное вычитаемое Случайные величины. Центральные тенденции меры разброса
Случайные величины. Центральные тенденции меры разброса Линейное уравнение с одной переменной
Линейное уравнение с одной переменной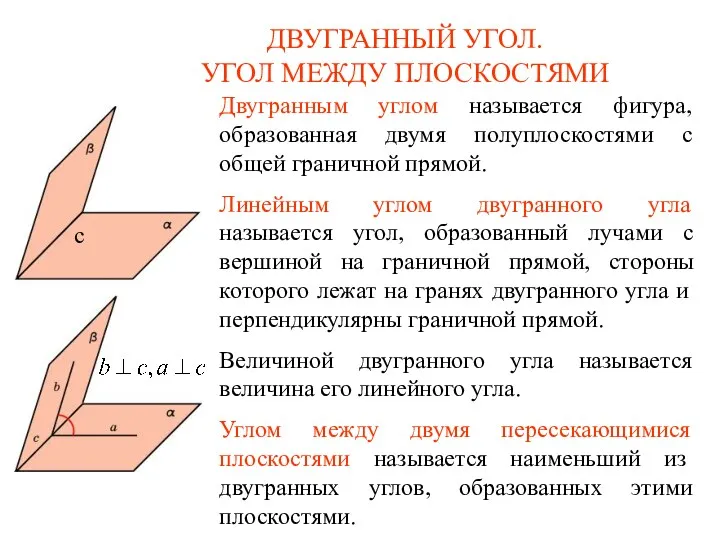 Двугранный угол. Угол между плоскостями
Двугранный угол. Угол между плоскостями Умножение трёхзначного числа на однозначное
Умножение трёхзначного числа на однозначное Измерение углов
Измерение углов