Содержание
- 2. Для доказательства используются признаки равенства прямоугольных треугольников. Если угол, сторона, противолежащая этому углу, и высота, опущенная
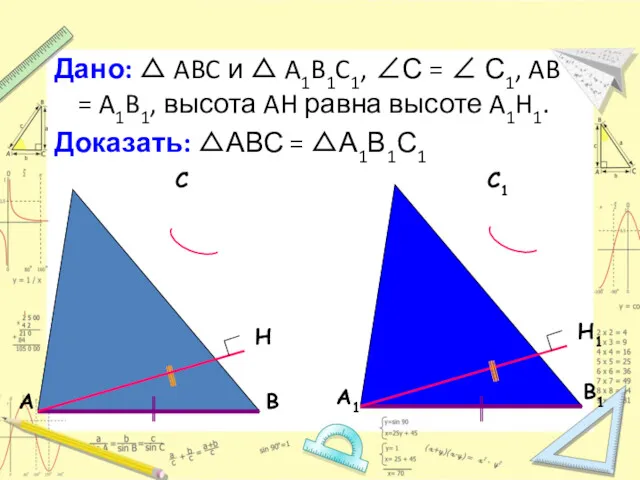
- 3. Дано: △ ABC и △ A1B1C1, ∠С = ∠ С1, AB = A1B1, высота AH равна
- 4. Доказательство: Прямоугольные △ ABH и △ A1B1H1 равны по катету и гипотенузе. Значит, ∠ B =
- 5. Если две стороны и медиана, заключенная между ними, одного треугольника соответственно равны двум сторонам и медиане
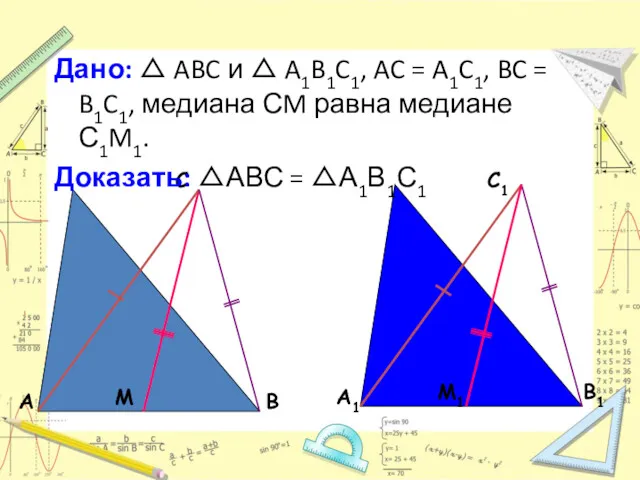
- 6. Дано: △ ABC и △ A1B1C1, AC = A1C1, BC = B1C1, медиана СM равна медиане
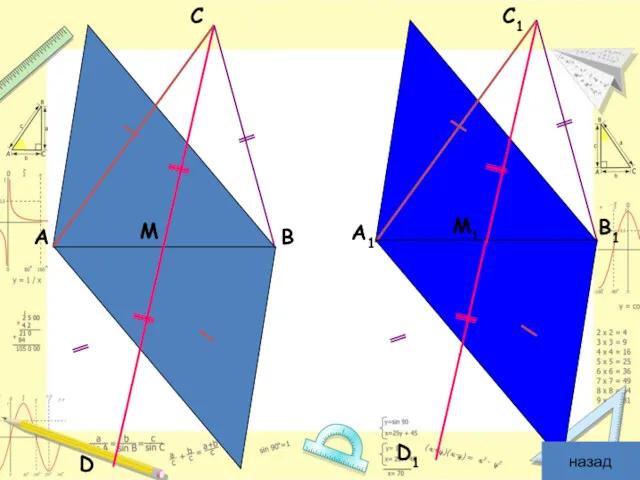
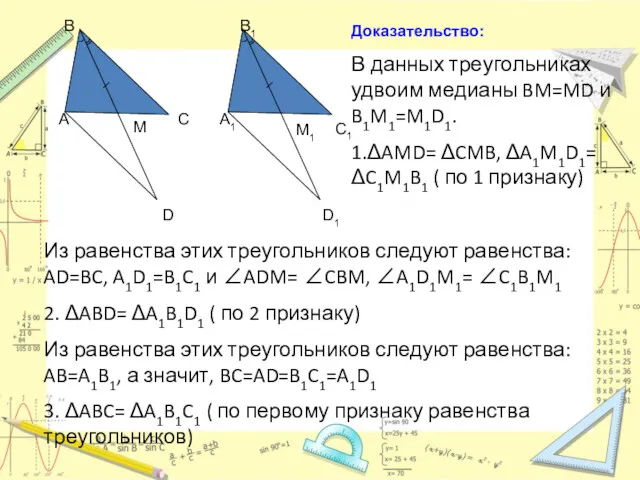
- 7. Доказательство: Продолжим медианы и отложим отрезки MD = CM и M1D1 = C1M1. Четырехугольники ACBD и
- 8. D D1 назад M M1
- 9. Если сторона и две медианы, проведенные к двум другим сторонам, одного треугольника соответственно равны стороне и
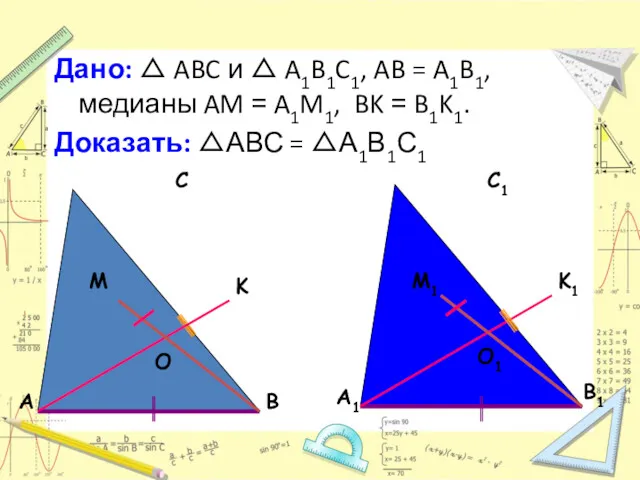
- 10. Дано: △ ABC и △ A1B1C1, AB = A1B1, медианы AM = A1M1, BK = B1K1.
- 11. Доказательство: Точки O и O1 пересечения медиан данных треугольников делят медианы в отношении 2 : 1,
- 12. Если две стороны и биссектриса, заключенная между ними, одного треугольника соответственно равны двум сторонам и биссектрисе,
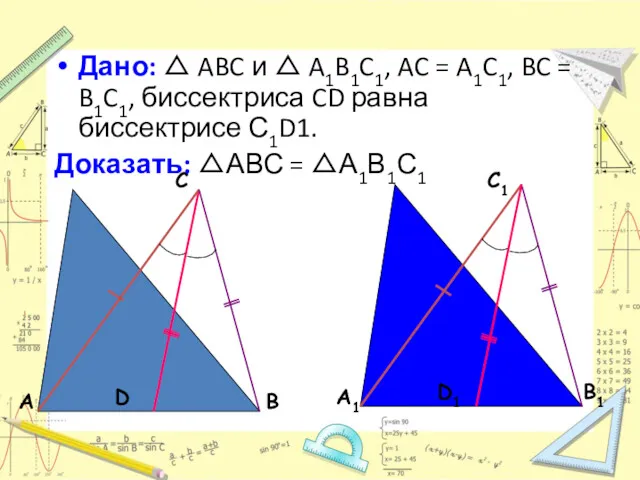
- 13. Дано: △ ABC и △ A1B1C1, AC = A1C1, BC = B1C1, биссектриса CD равна биссектрисе
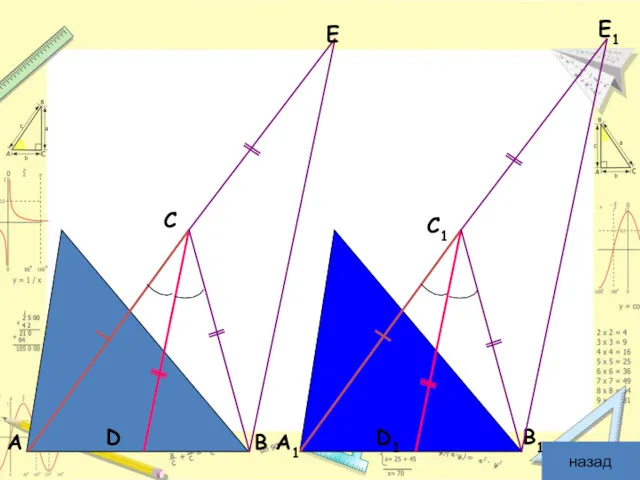
- 14. Доказательство: Продолжим стороны AC и A1C1 и отложим на их продолжениях отрезки CE = BC и
- 15. D D1 E E1 назад
- 16. Два треугольника равны, если сторона, медиана и высота, проведенные к другой стороне, одного треугольника соответственно равны
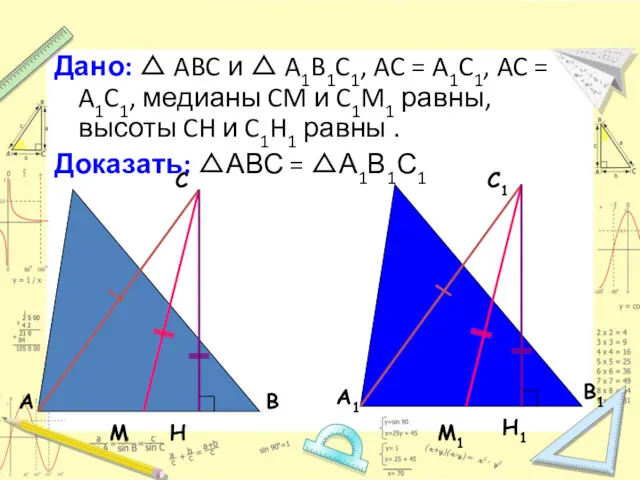
- 17. Дано: △ ABC и △ A1B1C1, AC = A1C1, AC = A1C1, медианы CM и C1M1
- 18. Доказательство: Прямоугольные △ ACH = △A1C1H1 по гипотенузе и катету. Следовательно, ∠ A = ∠ A1
- 19. Два треугольника равны, если медиана и два угла на которые делит угол медиана, одного треугольника соответственно
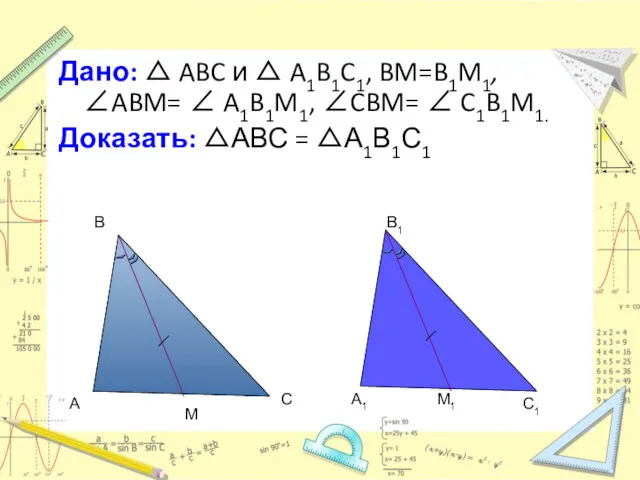
- 20. A B C M B1 A1 M1 C1 Дано: △ ABC и △ A1B1C1, BM=B1M1, ∠ABM=
- 21. Доказательство: В данных треугольниках удвоим медианы BM=MD и B1M1=M1D1. 1.ΔAMD= ΔCMB, ΔA1M1D1= ΔC1M1B1 ( по 1
- 22. Два треугольника равны, если сторона, и две высоты, опущенные на две другие стороны, одного треугольника соответственно
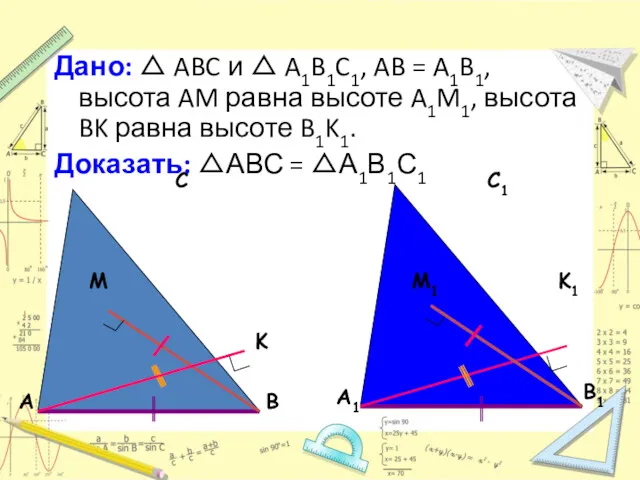
- 23. Дано: △ ABC и △ A1B1C1, AB = A1B1, высота AM равна высоте A1M1, высота BK
- 24. Доказательство: Из равенства прямоугольных треугольников △ AMB = △ A1M1B1, △ BKA = △B1K1A1 (по катету
- 25. Два треугольника равны, если три медианы одного треугольника соответственно равны трем медианам другого. Теорема 8
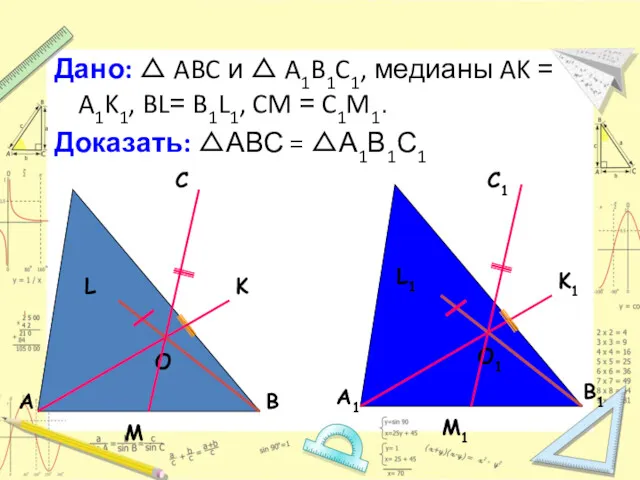
- 26. Дано: △ ABC и △ A1B1C1, медианы AK = A1K1, BL= B1L1, CM = C1M1. Доказать:
- 27. Доказательство: Пусть O и O1 — точки пересечения медиан данных треугольников. Заметим, что медианы OM и
- 28. Два треугольника равны, если три высоты одного треугольника соответственно равны трем высотам другого треугольника. Теорема 9
- 29. Дано: △ ABC и △ A1B1C1, AB = A1B1, высоты AH = A1H1, BG = B1G1,
- 31. Скачать презентацию

















 Сложение отрицательных чисел. Самостоятельная работа
Сложение отрицательных чисел. Самостоятельная работа Основные теоремы дифференциального исчисления: теорема Лагранжа
Основные теоремы дифференциального исчисления: теорема Лагранжа Формула объема прямоугольного параллелепипеда
Формула объема прямоугольного параллелепипеда Представьте числа в виде суммы разрядных слагаемых
Представьте числа в виде суммы разрядных слагаемых Рівняння прямої
Рівняння прямої Решение квадратных неравенств. Задания, сводящиеся к решению квадратных неравенств
Решение квадратных неравенств. Задания, сводящиеся к решению квадратных неравенств Первообразная и неопределенный интеграл
Первообразная и неопределенный интеграл Анализ эмпирических данных. (Тема 9)
Анализ эмпирических данных. (Тема 9)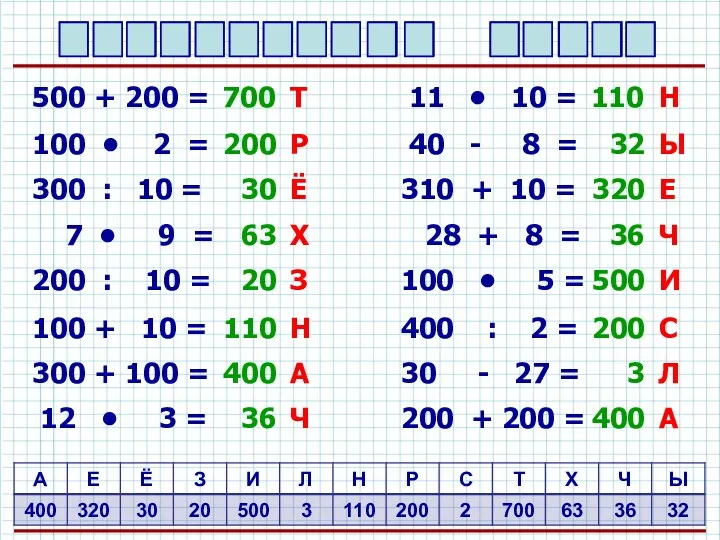 Трехзначные числа
Трехзначные числа Конспект урока математики в 4 классе по теме Деление на двузначное число
Конспект урока математики в 4 классе по теме Деление на двузначное число Системы линейных уравнений. Лекция 2
Системы линейных уравнений. Лекция 2 Наибольший общий делитель. Взаимно простые числа. 6 класс
Наибольший общий делитель. Взаимно простые числа. 6 класс Взаимосвязь между скоростью, временем и расстоянием. Урок математики в 5 классе
Взаимосвязь между скоростью, временем и расстоянием. Урок математики в 5 классе Расчетно-пояснительная записка
Расчетно-пояснительная записка Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций Теорія ймовірності
Теорія ймовірності Теорема Пифагора. По учебнику Л.С.Атанасян. 7 - 9 класс
Теорема Пифагора. По учебнику Л.С.Атанасян. 7 - 9 класс Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Laplace Transform
Laplace Transform Площадь треугольника и четырехугольника
Площадь треугольника и четырехугольника Скрещивающиеся прямые
Скрещивающиеся прямые Умножение и деление десятичных дробей
Умножение и деление десятичных дробей Раскрытие скобок. Математика. 6 класс
Раскрытие скобок. Математика. 6 класс Булевы функции и алгебра логики. Двойственность булевых функций
Булевы функции и алгебра логики. Двойственность булевых функций Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Формулы для вычисления площади треугольника
Формулы для вычисления площади треугольника Действия с десятичными дробями. Тестирование
Действия с десятичными дробями. Тестирование Умножение дробей. Знакомство с друзьями из Британии
Умножение дробей. Знакомство с друзьями из Британии