Содержание
- 2. Точка х1 называется точкой минимума функции f(x), если в некоторой окрестности точки х1 выполняется неравенство Значения
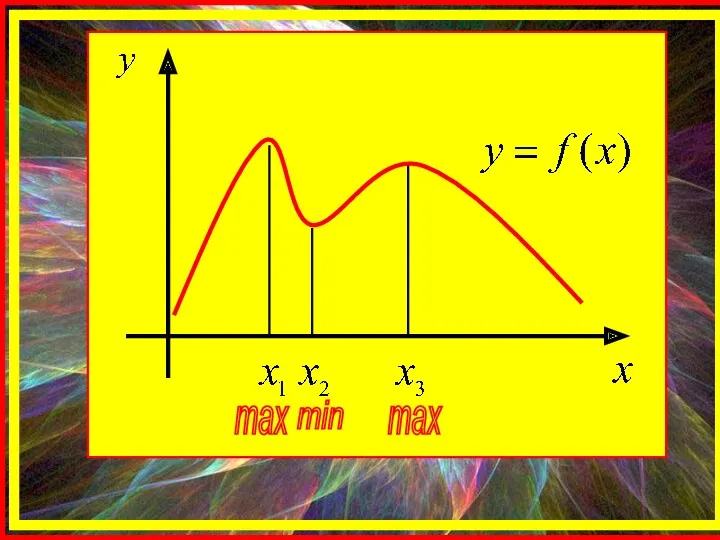
- 3. max min max
- 4. На одном промежутке функция может иметь несколько экстремумов, причем может быть, что минимум в одной точке
- 5. Однако, функция может иметь экстремум в точке, в которой она не дифференцируема. Например, функция имеет минимум
- 6. Для того, чтобы функция y=f(x) имела экстремум в точке х0 , необходимо, чтобы ее производная в
- 7. Точки, в которых выполняется необходимое условие экстремума, называются критическими или стационарными. Т.об., если в какой-либо точке
- 8. Найти критические точки и экстремумы функций: 1 Примеры
- 9. Решение: Применим необходимое условие экстремума: - критическая точка
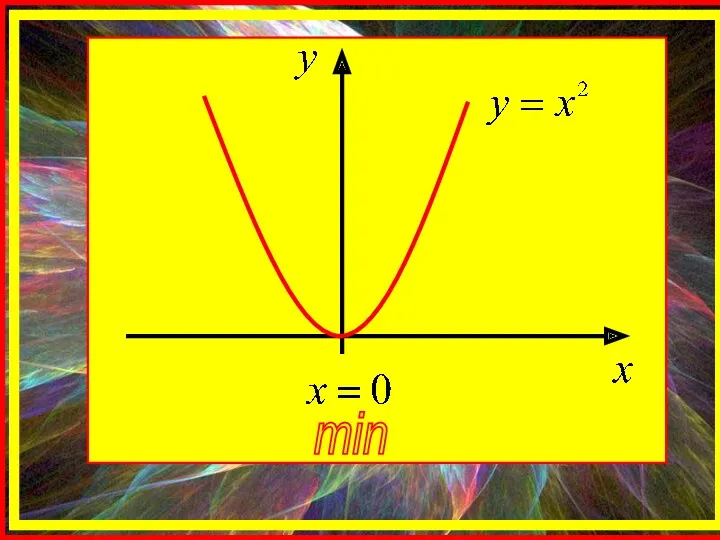
- 10. min
- 11. 2
- 12. Решение: Применим необходимое условие экстремума: - критическая точка
- 14. Если при переходе через точку х0 производная дифференцируемой функции y=f(x)меняет знак с плюса на минус, то
- 15. Доказательство: Пусть производная меняет знак с плюса на минус, т.е. на некотором интервале а на некотором
- 16. и будет убывать на По определению возрастающей функции Для убывающей функции -точка максимума. Аналогично доказывается для
- 17. 1 Найти производную функции 2 Найти критические точки функции, в которых производная равна нулю или не
- 18. 3 Исследовать знак производной слева и справа от каждой критической точки. 4 Найти экстремум функции.
- 19. Исследовать функцию на экстремум: Пример
- 20. Решение: Применим схему исследования функции на экстремум: 1 Находим производную функции:
- 21. 2 Находим критические точки: критические точки
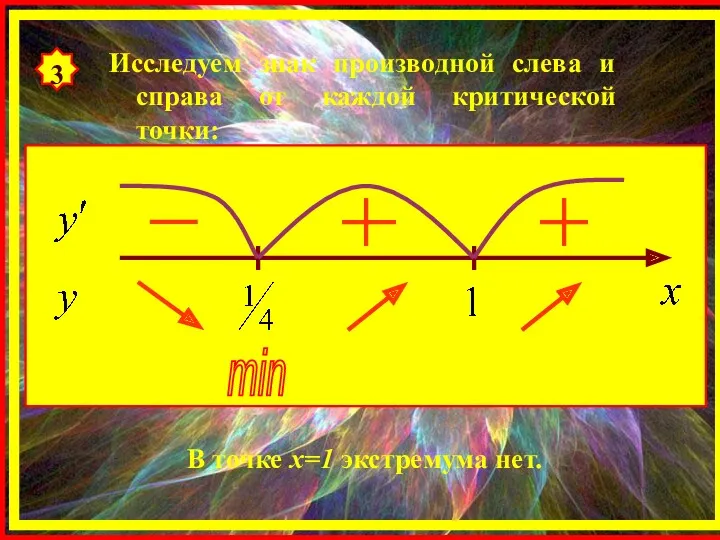
- 22. 3 Исследуем знак производной слева и справа от каждой критической точки: min В точке х=1 экстремума
- 23. 4 Находим экстремум функции:
- 24. Если первая производная дифференцируемой функции y=f(x) в точке х0 равна нулю, а вторая производная в этой
- 25. Доказательство: Пусть следовательно и в некоторой окрестности точки х0, т.е.
- 26. функция будет возрастать на содержащем точку х0. Но на интервале а на интервале
- 27. Таким образом, функция при переходе через точку х0 меняет знак с минуса на плюс, следовательно эта
- 28. Схема исследования функции на экстремум в этом случае аналогична предыдущей, но третий пункт следует заменить на:
- 30. Скачать презентацию
















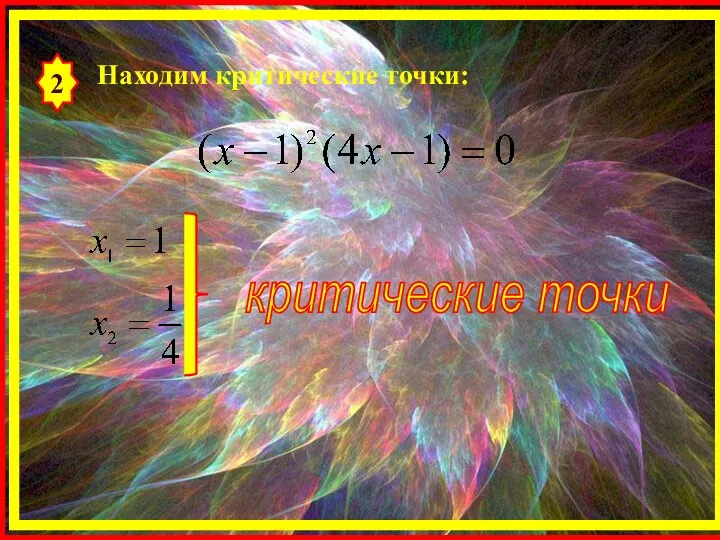






 Подготовка к ЕГЭ. Задача В13
Подготовка к ЕГЭ. Задача В13 Таблиця множення числа 3
Таблиця множення числа 3 Величины. Таблица единиц площади.
Величины. Таблица единиц площади. Прибавление числа 3
Прибавление числа 3 Задачи на готовых чертежах. Четырехугольники
Задачи на готовых чертежах. Четырехугольники Устные вычисления в пределах 1000
Устные вычисления в пределах 1000 Презентация к уроку математики по теме Решение уравнений
Презентация к уроку математики по теме Решение уравнений Диэлектрическая проницаемость сред с временной и пространственной дисперсией. (Лекция 3)
Диэлектрическая проницаемость сред с временной и пространственной дисперсией. (Лекция 3) Окружность, круг и их элементы
Окружность, круг и их элементы Презентация к уроку математики в 4 классе.Деление на двузначные и трёхзначные числа.
Презентация к уроку математики в 4 классе.Деление на двузначные и трёхзначные числа. Решение задач с помощью графов
Решение задач с помощью графов Свойства степени с натуральным показателем. 7 класс
Свойства степени с натуральным показателем. 7 класс Предел последовательности
Предел последовательности Веселая математика
Веселая математика Порядок выполнения действий в примерах. Закрепление
Порядок выполнения действий в примерах. Закрепление Решение задач на проценты (5 класс)
Решение задач на проценты (5 класс) Представление рациональных чисел в виде десятичной дроби (продолжение)
Представление рациональных чисел в виде десятичной дроби (продолжение) Теорема Піфагора
Теорема Піфагора Сложение и вычитание в пределах 20. Закрепление
Сложение и вычитание в пределах 20. Закрепление Длина окружности. Площадь круга
Длина окружности. Площадь круга счёт
счёт Веселый счет
Веселый счет Математика в моей жизни. 6 класс
Математика в моей жизни. 6 класс Линейная функция и её график
Линейная функция и её график Развитие логического мышления младших школьников посредством решения нестандартных задач
Развитие логического мышления младших школьников посредством решения нестандартных задач Урок математики по теме Длина ломаной. Периметр с презентацией
Урок математики по теме Длина ломаной. Периметр с презентацией Окружность и круг. Сфера и шар
Окружность и круг. Сфера и шар Презентация к уроку математики Периметр многоугольника
Презентация к уроку математики Периметр многоугольника