Функции и их свойства. Предел последовательности и функции. Производная функции и дифференциал презентация
Содержание
- 10. График четной функции симметричен относительно оси а нечетной − относительно точки С (0;0), т.е. начала координат.
- 15. Кратко определение предела можно записать так:
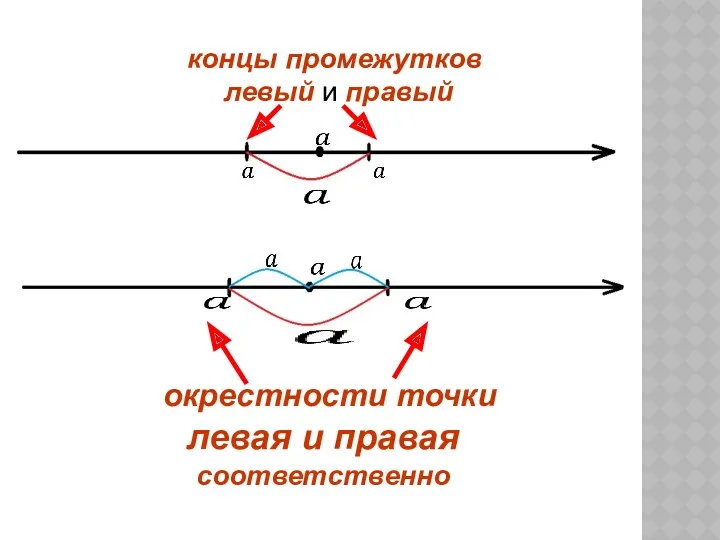
- 16. Геометрический смысл определения предела последовательности: Неравенство равносильно неравенствам или т.е. Поэтому определение предела последовательности можно сформулировать
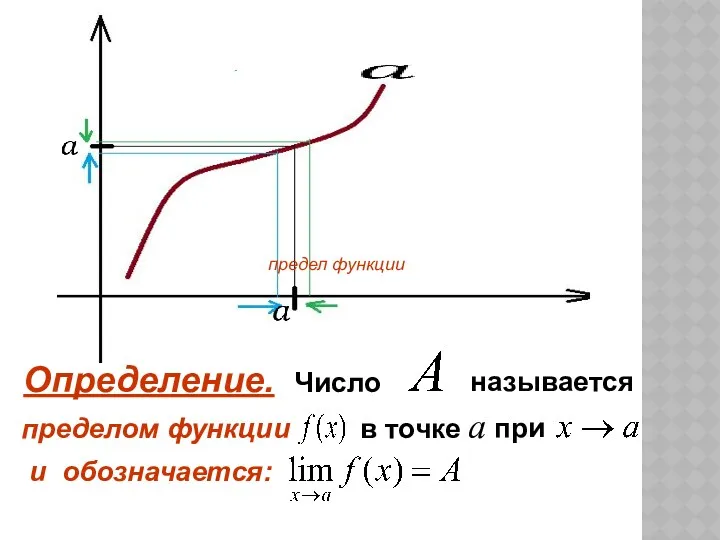
- 18. Предел функции в точке. Бесконечно большая и бесконечно малая функция.
- 26. А если условия этой теоремы не выполнены, то могут возникнуть неопределенности вида : которые в простейших
- 33. ПРОИЗВОДНАЯ ФУНКЦИИ Определение производной Геометрический смысл производной Связь между непрерывностью и дифференцируемостью Производные основных элементарных функций
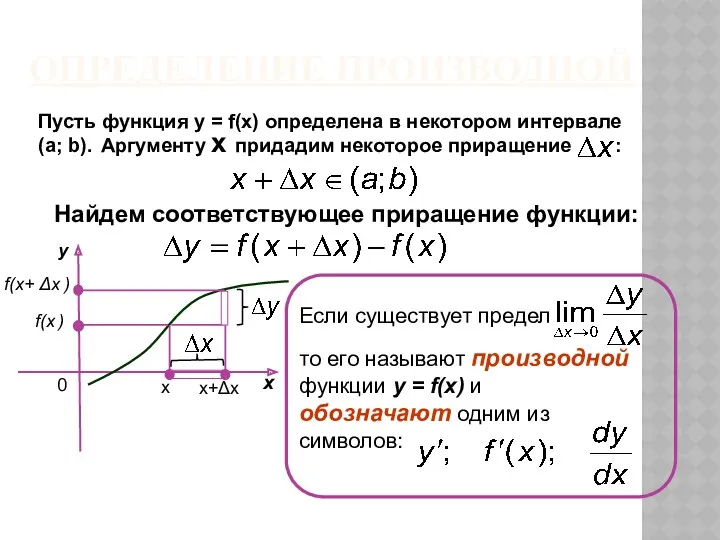
- 34. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ Найдем соответствующее приращение функции:
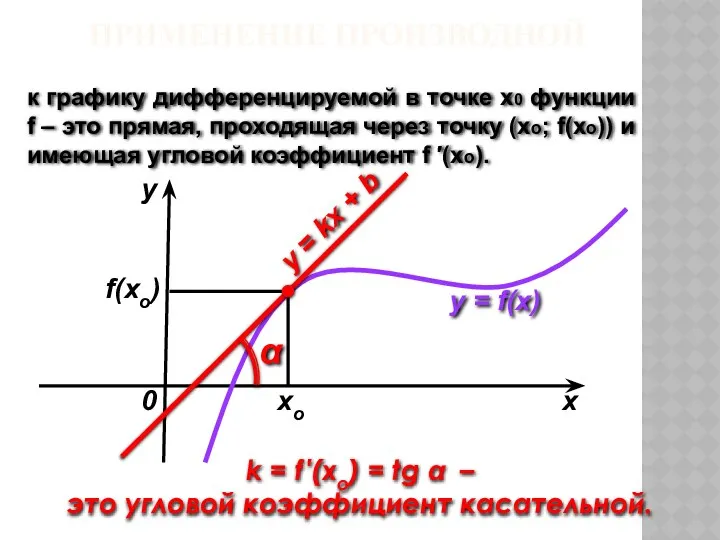
- 35. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
- 36. Если точка касания М имеет координаты (x0; y0 ), угловой коэффициент касательной есть k = f
- 37. СВЯЗЬ МЕЖДУ НЕПРЕРЫВНОСТЬЮ И ДИФФЕРЕНЦИРУЕМОСТЬЮ ФУНКЦИИ Если функция f(x) дифференцируема в некоторой точке , то она
- 38. Нахождение производной называют дифференцированием
- 39. ТАБЛИЦА ПРОИЗВОДНЫХ
- 40. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ Пусть u(x) , v(x) и w(x) – дифференцируемые в некотором интервале (a; b) функции,
- 41. ПРАВИЛА НАХОЖДЕНИЯ ПРОИЗВОДНОЙ 1. Если функции u(x) и v(x) имеют в точке х производные, то их
- 42. ПРАВИЛА НАХОЖДЕНИЯ ПРОИЗВОДНОЙ 3. Если функции u(x) и v(x) имеют в точке х производные, то их
- 43. ПРАВИЛА НАХОЖДЕНИЯ ПРОИЗВОДНОЙ 5. Если функции u(x) и v(x) имеют в точке х производные и v(x)
- 44. ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ Пусть y = f(u) и u = φ(x) , тогда y = f(φ(x))
- 45. ПРИМЕР Вычислить производную функции
- 46. ПРИМЕР: Вычислить производную функции: Данную функцию можно представить следующим образом: Коротко:
- 47. k = f ′(xo) = tg α – это угловой коэффициент касательной. Касательная к графику дифференцируемой
- 48. Общий вид уравнения касательной y = f ′(xo)(x – xo) + f(xo) Алгоритм составления уравнения касательной
- 49. Одна из основных задач исследования функции – это нахождение промежутков её возрастания и убывания. Признак возрастания
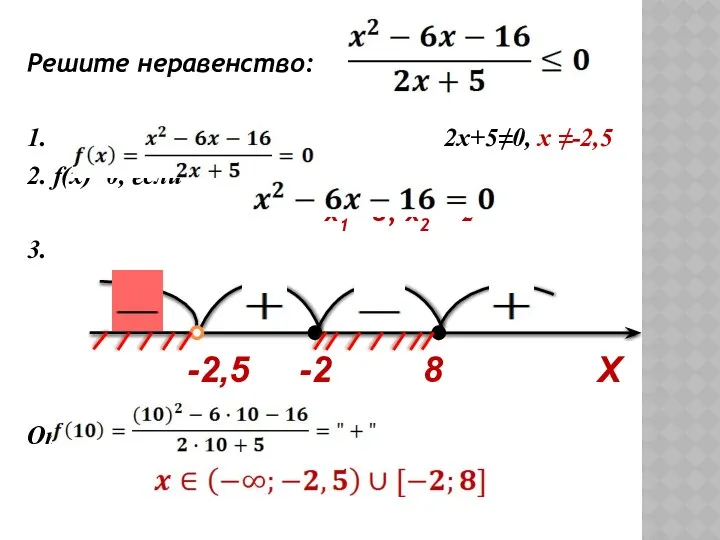
- 50. АЛГОРИТМ РЕШЕНИЯ НЕРАВЕНСТВ МЕТОДОМ ИНТЕРВАЛОВ: Выделить функцию y=f(x). Найти область определения функции D(f). Указать промежутки непрерывности.
- 51. Решите неравенство: 1. 2x+5≠0, х ≠-2,5 2. f(x)=0, если x1= 8, x2= -2 3. Ответ:
- 52. АЛГОРИТМ НАХОЖДЕНИЯ ПРОМЕЖУТКОВ ВОЗРАСТАНИЯ (УБЫВАНИЯ) ФУНКЦИИ y=f(x): Найти производную функции f´(x). Решить уравнение f´ (x) =0.
- 53. Найдите промежутки возрастания и убывания функции: 1. 2. f´(x)=0, если 3. Ответ:
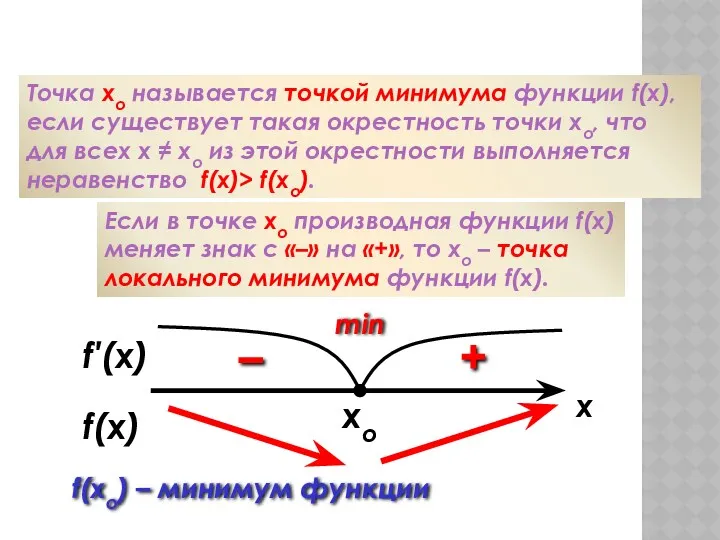
- 54. f′(x) xo Минимум функции Точка хо называется точкой минимума функции f(x), если существует такая окрестность точки
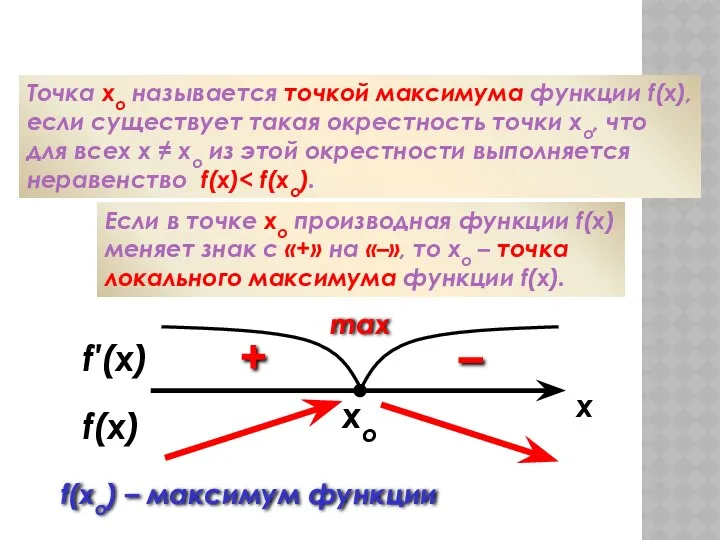
- 55. xo Максимум функции Точка хо называется точкой максимума функции f(x), если существует такая окрестность точки хо,
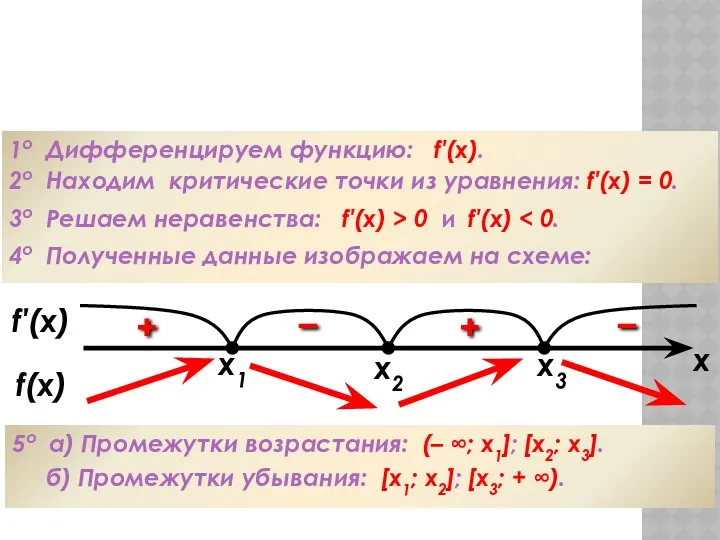
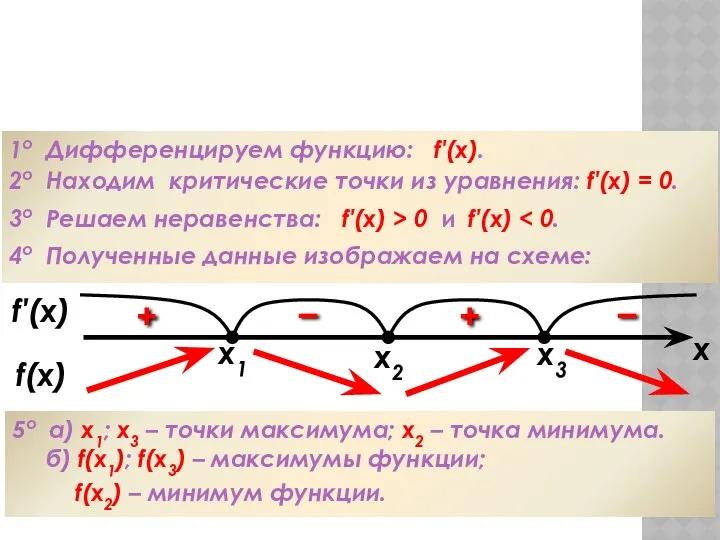
- 56. Алгоритм исследования функции на монотонность 1о Дифференцируем функцию: f′(x). 2о Находим критические точки из уравнения: f′(x)
- 57. Алгоритм исследования функции на экстремумы 1о Дифференцируем функцию: f′(x). 2о Находим критические точки из уравнения: f′(x)
- 58. ПРИМЕРЫ
- 61. Скачать презентацию


















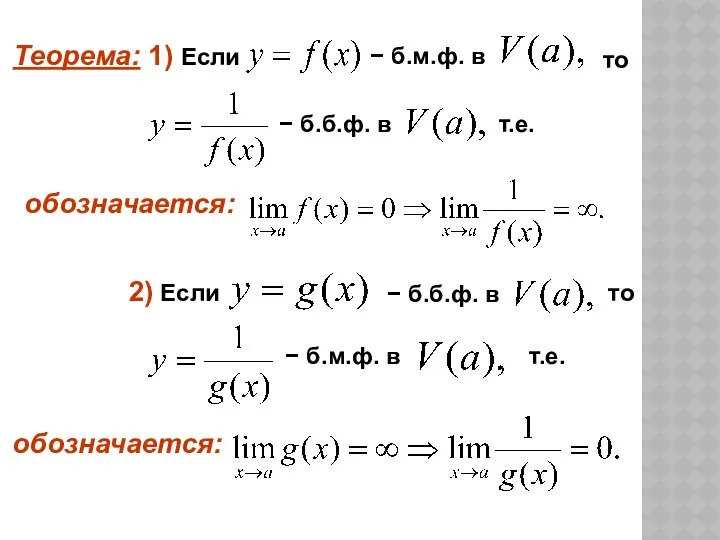


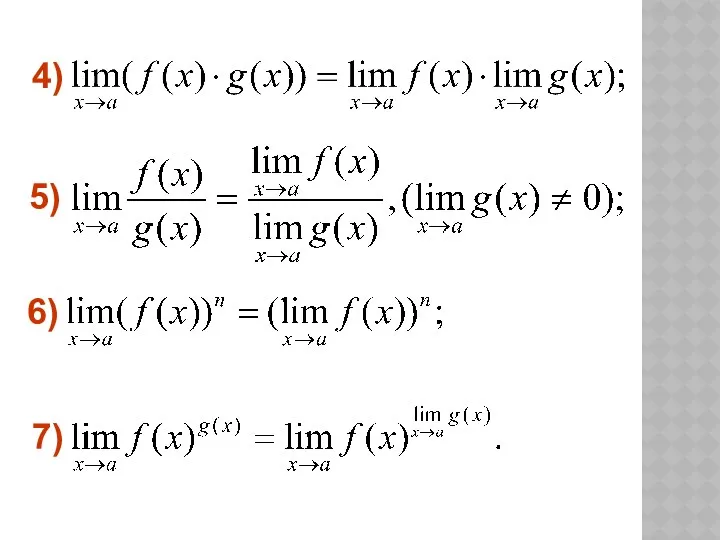





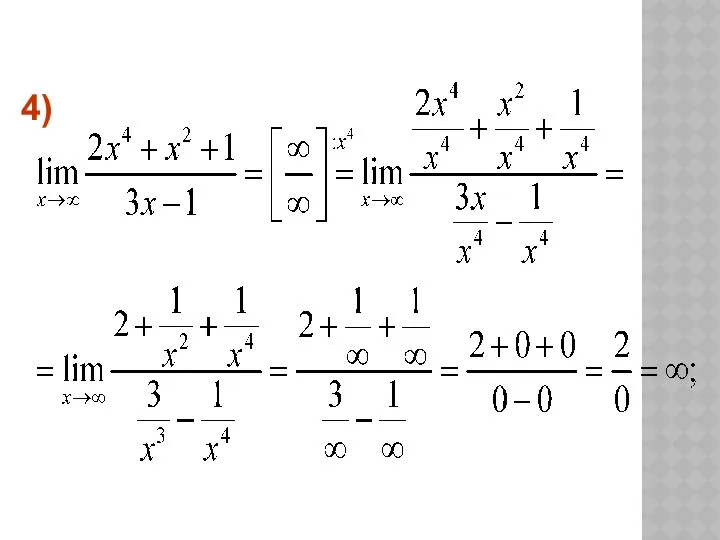






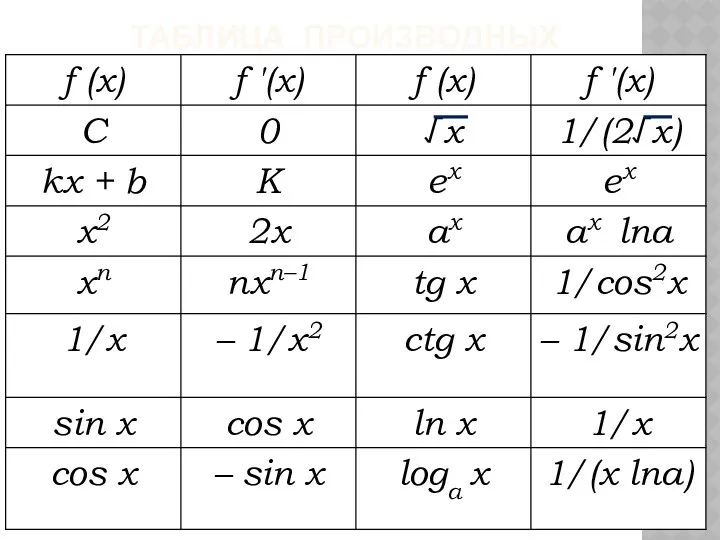












 Математическая смекалка
Математическая смекалка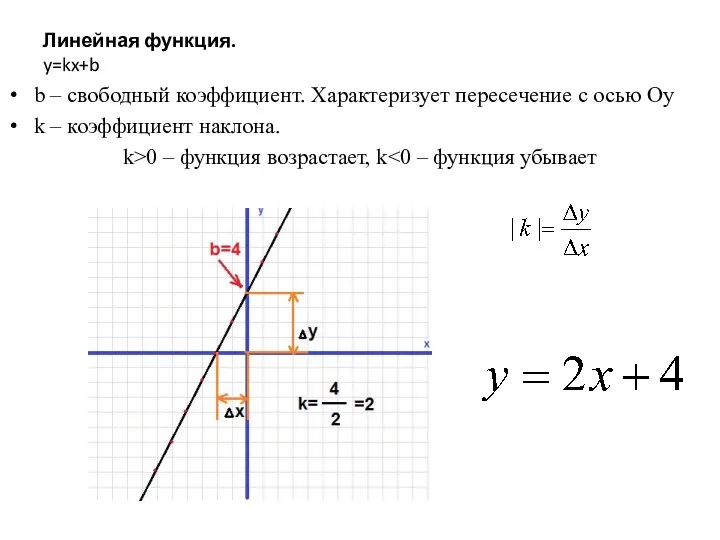 Линейная функция y=kx+b
Линейная функция y=kx+b Прямая и обратная пропорциональные зависимости
Прямая и обратная пропорциональные зависимости Однозначные и двузначные числа. Сравнение чисел
Однозначные и двузначные числа. Сравнение чисел Пропорции. Задание для устного счета. Упражнение 17. 6 класс
Пропорции. Задание для устного счета. Упражнение 17. 6 класс Математическая раскраска Маша и медведь
Математическая раскраска Маша и медведь Презентация к уроку математики Приметр многоугольника.
Презентация к уроку математики Приметр многоугольника. Измерение отрезков. Блиц-опрос. Геометрия 7 класс
Измерение отрезков. Блиц-опрос. Геометрия 7 класс Объём фигуры. Единицы объёма
Объём фигуры. Единицы объёма Законы распределения случайных величин. Лекция 2
Законы распределения случайных величин. Лекция 2 Сумма углов треугольника
Сумма углов треугольника ДЕМО вариант 2016
ДЕМО вариант 2016 Параллелепипеды. Прямоугольные параллелепипеды. Куб
Параллелепипеды. Прямоугольные параллелепипеды. Куб Учимся прибавлять к 9, 8, 7 и 6 +6
Учимся прибавлять к 9, 8, 7 и 6 +6 Звичайні дроби
Звичайні дроби тест по математике № 1 - 1 класс
тест по математике № 1 - 1 класс Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда Устный счет
Устный счет ГИА - 2012. Открытый банк заданий по математике. Задача №15
ГИА - 2012. Открытый банк заданий по математике. Задача №15 Рациональные числа
Рациональные числа Комплексные числа
Комплексные числа 20190306_reshenie_uravneniy
20190306_reshenie_uravneniy Конспект урока математики по теме: Умножение числа 3 на однозначные числа. 2 класс. УМК Перспективная начальная школа
Конспект урока математики по теме: Умножение числа 3 на однозначные числа. 2 класс. УМК Перспективная начальная школа Смешанные числа
Смешанные числа Презентация Весёлые задачки для 1 класса.
Презентация Весёлые задачки для 1 класса. Натуральные числа. Как записывают и читают натуральные числа
Натуральные числа. Как записывают и читают натуральные числа Величины. Таблица единиц площади.
Величины. Таблица единиц площади. Сумма углов треугольника
Сумма углов треугольника