Слайд 2

Слайд 3

Слайд 4
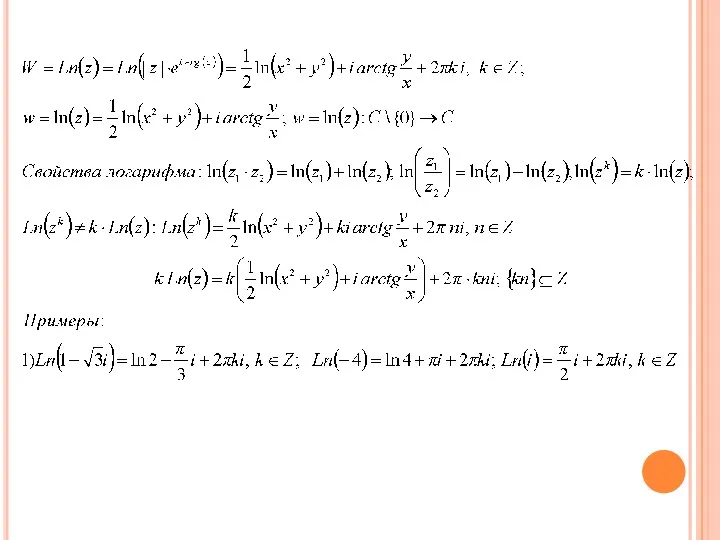
Слайд 5

Слайд 6

Слайд 7

Примеры С-дифф. и не дифф. функций
1)f(z)=2x-3iy; u(x,y)=2x; v(x,y)=-3y;
2) f(z)=|z|2=x2+y2;
Слайд 8

Слайд 9

Применение условий коши -Римана
Слайд 10
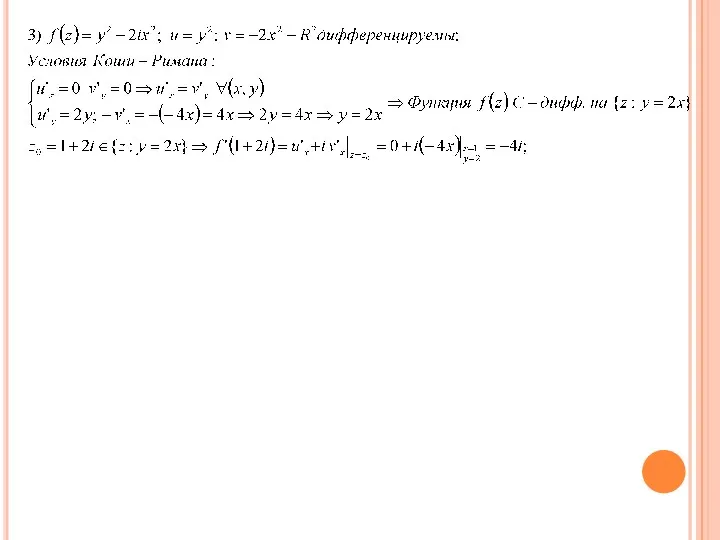
Слайд 11

Примеры функций:
4) f(z)=ez;
Теорема.
Все элементарные функции комплексного переменного имеют те же
производные, что и для функций действительного переменного.
Слайд 12

Голоморфные или аналитические функции
Слайд 13

Введем обозначение:
H(D)- множество функций, аналитичных
( голоморфных: holomorphic) в области D
Слайд 14

Свойства аналитических(голоморфных) функций
Слайд 15
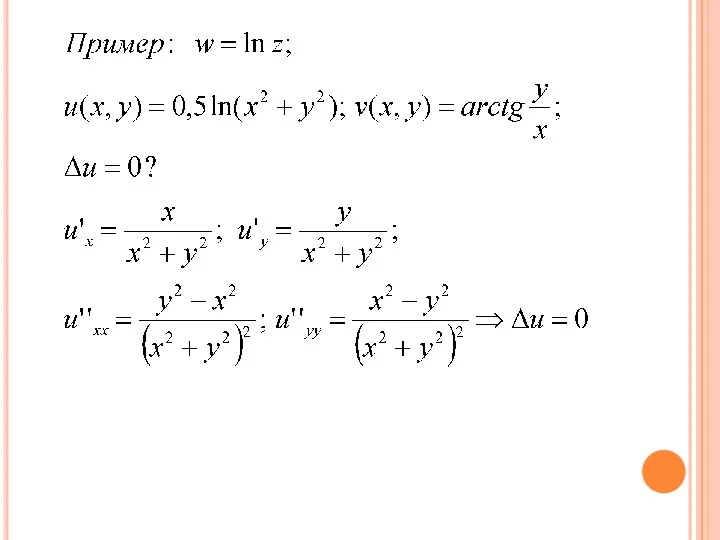
Слайд 16

Слайд 17

Свойства аналитических функций
Слайд 18

Слайд 19

Восстановить функцию по её известной действительной части:
Слайд 20

2) Восстановить функцию f(z) по известной мнимой части и условию f(-i)=2i;
Слайд 21

3) Можно ли восстановить функцию f(z)∊H(C), если
3.1.
3.2.
Ответ: да, если эти
функции гармонические:
?u=0⟶u(x,y)=?
?v=0⟶v(x,y)=C1xy+C2;да, восстановить можно;
Слайд 22

Слайд 23

Геометрический смысл С-дифференцируемости
Слайд 24

Слайд 25

Слайд 26

Слайд 27

Определение.
Отображение, сохраняющее углы между кривыми в точке z=a при отображении f(z),
называется конформным.
Теорема.
Если f(z)∊H(D); z=a ∊ D и f ’(a) ≠0, тогда отображение w=f(z) конформно в точке z=a.
Вывод: все аналитические функции являются конформными отображениями.
Слайд 28

Слайд 29

Слайд 30

Слайд 31

Слайд 32

Слайд 33

Слайд 34

Слайд 35

Слайд 36



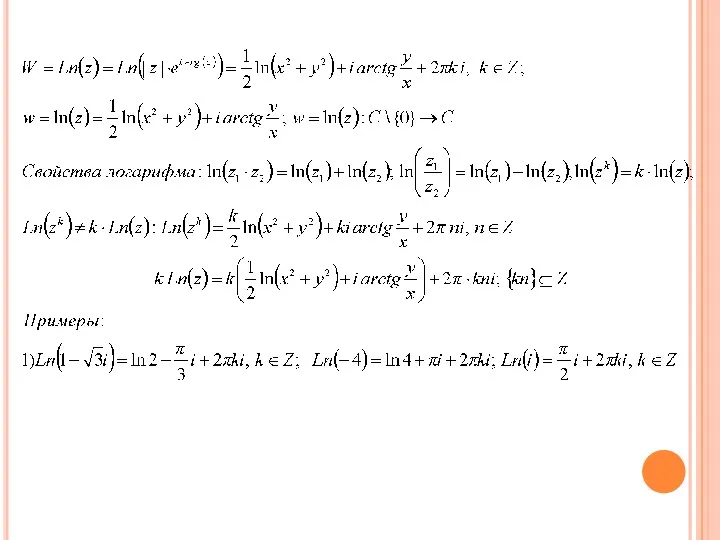





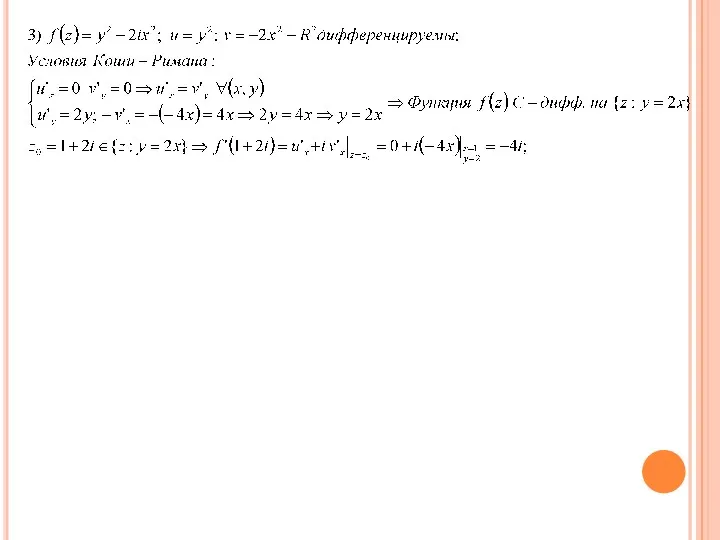




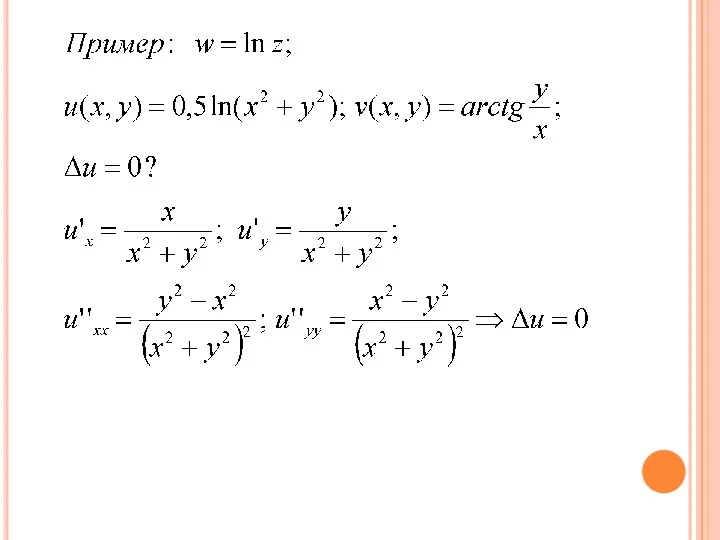





















 Математические ребусы
Математические ребусы Решение нестандартных задач для подготовки к олимпиаде по математике в начальной школе
Решение нестандартных задач для подготовки к олимпиаде по математике в начальной школе Изучаем геометрические фигуры. Дидактическая игра На что похоже?
Изучаем геометрические фигуры. Дидактическая игра На что похоже?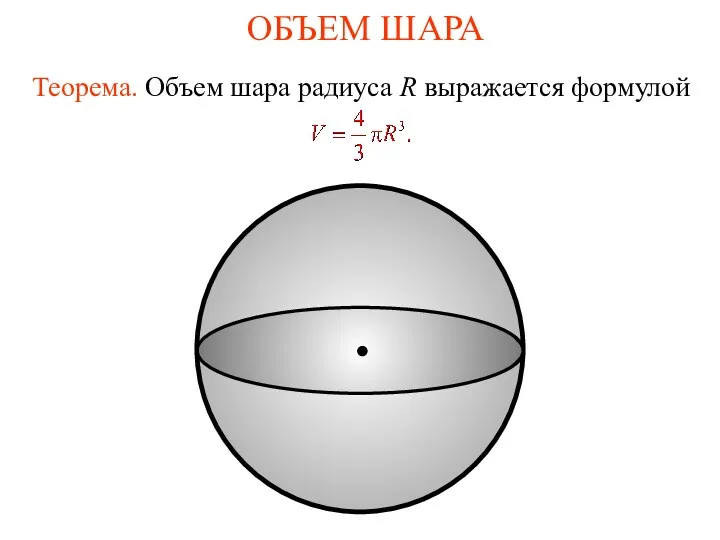 Объем шара
Объем шара Основное свойство дроби. 5 класс
Основное свойство дроби. 5 класс Таблица умножения(ТРЕНАЖЕР)
Таблица умножения(ТРЕНАЖЕР) Конечные автоматы. Абстрактные и структурные автоматы. Синтез конечных автоматов и МПА
Конечные автоматы. Абстрактные и структурные автоматы. Синтез конечных автоматов и МПА Сравнение предметов.
Сравнение предметов. Задачи на проценты
Задачи на проценты Статистика – дизайн информации
Статистика – дизайн информации Теорема о соотношениях между сторонами и углами треугольника
Теорема о соотношениях между сторонами и углами треугольника Аргументация и логическая прагматика
Аргументация и логическая прагматика Нахождение числа по его дроби. 6 класс
Нахождение числа по его дроби. 6 класс Преобразование комплексного чертежа
Преобразование комплексного чертежа Решение тригонометрических уравнений и способы отбора корней на заданном промежутке
Решение тригонометрических уравнений и способы отбора корней на заданном промежутке Методы решения тригонометрических уравнений
Методы решения тригонометрических уравнений Задачи по экологии
Задачи по экологии Меры разброса
Меры разброса Урок Числа от 10 до 20
Урок Числа от 10 до 20 Моделирование в электронных таблицах. График и свойства квадратичной функции
Моделирование в электронных таблицах. График и свойства квадратичной функции Предмет математического анализа
Предмет математического анализа Учимся считать. Считалочка козленок. Третий уровень сложности
Учимся считать. Считалочка козленок. Третий уровень сложности Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Тест по теме: Тетраэдр и параллелепипед. Теория
Тест по теме: Тетраэдр и параллелепипед. Теория Внеурочная деятельность. Математические ребусы. (2-3 класс)
Внеурочная деятельность. Математические ребусы. (2-3 класс) Случайные эксперименты (опыты) и случайные события. Элементарные события (исходы)
Случайные эксперименты (опыты) и случайные события. Элементарные события (исходы) Математика о вреде курения. Урок-проблема для 7 класса часть 1
Математика о вреде курения. Урок-проблема для 7 класса часть 1 Контурный анализ
Контурный анализ