Содержание
- 2. Правило суммы Если элемент x можно выбрать способами nx и если элемент y можно выбрать ny
- 3. Правило суммы Правило суммы используется тогда, когда варианты соединяются словом «ИЛИ»
- 4. Пример 1 Сколько различных символов можно закодировать, используя код Морзе длиной не менее 5 и (или)
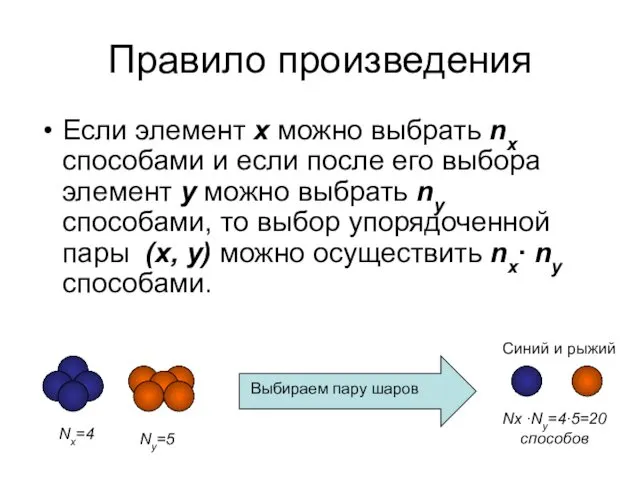
- 5. Правило произведения Если элемент x можно выбрать nx способами и если после его выбора элемент y
- 6. Пример 2. Номер автомобиля состоит из шести мест, на первом – буква, затем – три цифры,
- 7. Формулы комбинаторики Перестановки Размещения Сочетания
- 8. Два главных вопроса В задаче требуется переставить все элементы или требуется выбрать несколько из них? (все
- 9. Перестановки Используются все элементы Порядок элементов важен
- 10. Перестановки без повторений Перестановками без повторений из n различных элементов называются все возможные последовательности этих n
- 11. Перестановки без повторений 6 различных перестановок
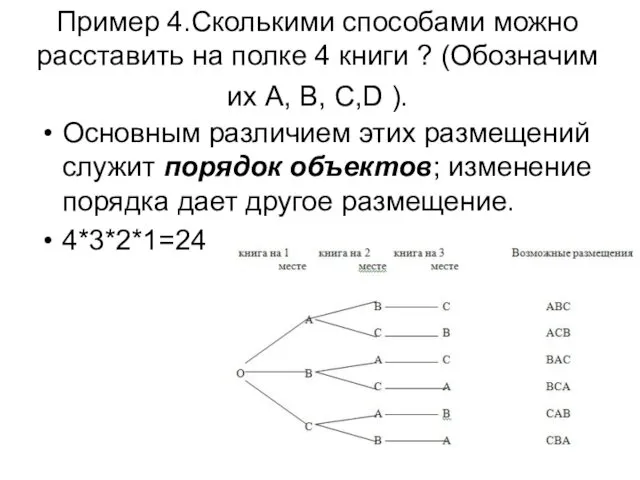
- 12. Пример 4.Сколькими способами можно расставить на полке 4 книги ? (Обозначим их А, В, С,D ).
- 13. Пример 5 По следствию должны пройти пять человек: A, B, C, D, E. Cколько вариантов того,
- 14. Решение АВ??? - таких вариантов Р3=3!=6 ?АВ?? ??АВ? ???АВ Всего вариантов М=6*4=24
- 15. Перестановки с повторениями Перестановки с повторением из n элементов k типов число элементов 1-го типа n1;
- 16. Перестановки с повторениями n1=2 n2=1 n=n1+n2=2+1=3 3 различные перестановки
- 17. Пример 6. Сколько чисел можно создать из двух цифр «2» и двух цифр «1»? 1122 1212
- 18. Пример 7. Существует конечное число неэквивалентных друг другу логических функций, зависящих от трех аргументов. Среди них
- 19. Решение 8!/(2!*6!)=23
- 20. Размещения (выборки) Используются не все элементы Порядок элементов важен
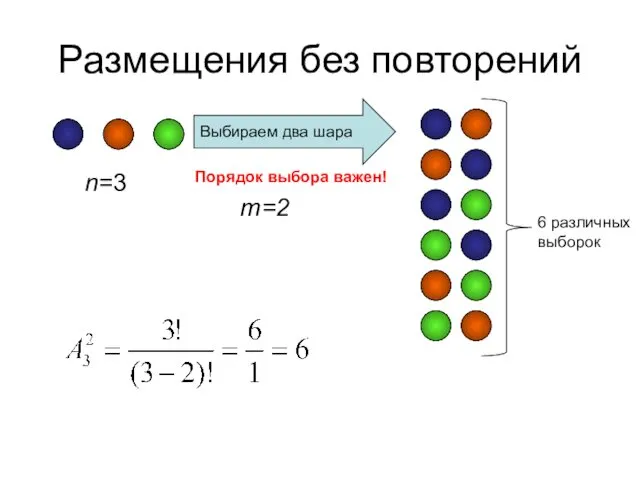
- 21. Размещения без повторений Размещениями без повторений из n различных элементов по m элементов называются все такие
- 22. Размещения без повторений n=3 Выбираем два шара m=2 Порядок выбора важен! 6 различных выборок
- 23. Пример 8 В фирме работают 8 человек одинаковой квалификации, среди них Иванов, Петров, Сидоров. Сколькими способами
- 24. Решение Всего вариантов - выбрать три из восьми без повторения, т.к. один и тот же не
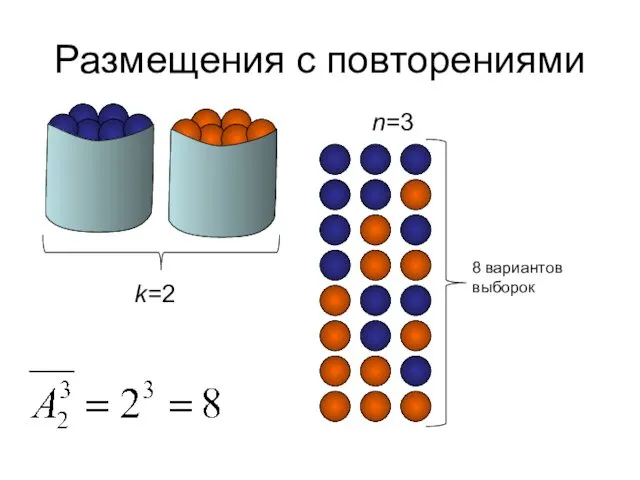
- 25. Размещения с повторениями Размещения с повторениями из элементов k типов по m элементов (k и m
- 26. Размещения с повторениями k=2 n=3 8 вариантов выборок
- 27. Пример 9 Замок камеры хранения имеет четыре диска, каждый из которых разделен на 10 секторов; на
- 28. Решение 1) Всего вариантов 2) Всего вариантов 3) Всего вариантов N=10*9*9*9
- 29. Сочетания Используются не все элементы Порядок элементов не важен
- 30. Сочетания без повторений Сочетаниями без повторений из n различных элементов по m элементов называются все такие
- 31. Сочетания без повторений n=3 Выбираем два шара m=2 Порядок выбора не важен! 3 сочетания
- 32. Пример 10 В чемпионате по шахматам участвовало 40 спортсменов. Каждый с каждым сыграл по одной партии.
- 33. Решение
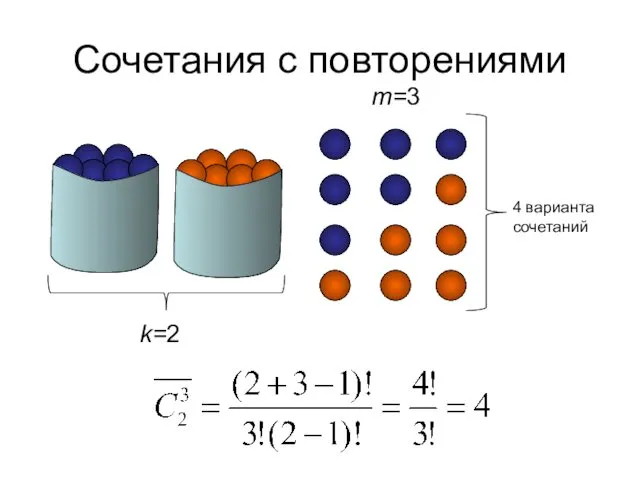
- 34. Сочетания с повторениями Сочетаниями с повторениями из элементов k типов по m элементов (m и k
- 35. Сочетания с повторениями k=2 m=3 4 варианта сочетаний
- 36. Пример 11 Имеется 2 типа цветов, количество цветов не ограничено. Сколько различных букетов можно составить из
- 37. Пример 12 Имеется 5 типов цветов, количество цветов не ограничено. Сколько различных букетов можно составить из
- 38. Решение Сочетание с повторением: (5+3-1)!/(3!*(5-1) !)=35
- 40. Пример 13. Сколькими способами можно выбрать четырех студентов, которые будут получать стипендию, из восьми. Решение. Мы
- 41. Пример 14. Паша, Сережа, Андрей и Антон думают надеть ли на торжественный вечер галстуки или бабочки.
- 42. Задача1 Световое табло состоит из лампочек. Каждая лампочка может находиться в одном из трех состояний («включено»,
- 43. Задача 2 Для передачи сигналов на флоте используются специальные сигнальные флаги, вывешиваемые в одну линию (последовательность
- 44. Задача 3 Вася и Петя передают друг другу сообщения, используя синий, красный и зеленый фонарики. Это
- 45. Задача 4 Для кодирования 300 различных сообщений используются 5 последовательных цветовых вспышек. Вспышки одинаковой длительности, для
- 46. Задача 5 Сколько существует четырехзначных чисел, в записи которых все цифры различны?
- 47. Задача 6 Виктор хочет купить пять разных книг, но денег у него хватает только на три
- 49. Скачать презентацию








































 Обобщающий урок по теме: Уравнения
Обобщающий урок по теме: Уравнения Свойства параллельных прямых
Свойства параллельных прямых Решение задач на проценты. Прежде чем закурить - подумай!
Решение задач на проценты. Прежде чем закурить - подумай! Производная
Производная Коэффициент. Приведение подобных слагаемых. 6 класс
Коэффициент. Приведение подобных слагаемых. 6 класс Презентация к уроку математики Деление с остатком
Презентация к уроку математики Деление с остатком Презентация Приемы вычислений для случае вида 36+4
Презентация Приемы вычислений для случае вида 36+4 Движение. Виды движения. Симметрия
Движение. Виды движения. Симметрия Повторение курса математики (7-9 класс)
Повторение курса математики (7-9 класс) Теорема Фалеса
Теорема Фалеса Типичные законы распределения вероятностей. Нормальное распределение. Показательное распределение. Равномерное распределение
Типичные законы распределения вероятностей. Нормальное распределение. Показательное распределение. Равномерное распределение Бизнес-игра по математике. 10-11 класс
Бизнес-игра по математике. 10-11 класс Делим числа урок 46
Делим числа урок 46 Основы математической статистики. Лекция 3
Основы математической статистики. Лекция 3 Системы линейных уравнений. Основные понятия
Системы линейных уравнений. Основные понятия Решение неравенств второй степени. Подготовка к ГИА. 9 класс
Решение неравенств второй степени. Подготовка к ГИА. 9 класс занятие 34 (42)
занятие 34 (42) Деление двузначного числа на однозначное.
Деление двузначного числа на однозначное. Описательная статистика
Описательная статистика Урок -путешествие
Урок -путешествие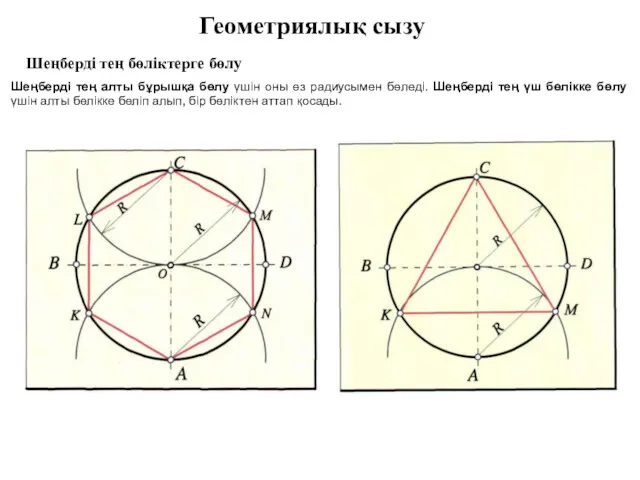 Геометриялық сызу
Геометриялық сызу Уравнение окружности (9 класс)
Уравнение окружности (9 класс) Признаки делимости на 3 и 9
Признаки делимости на 3 и 9 Решение задач. Подготовка к ЕГЭ
Решение задач. Подготовка к ЕГЭ Rescaling, sum and difference of random variables. (Lecture 4)
Rescaling, sum and difference of random variables. (Lecture 4) Статистические графики
Статистические графики Треугольники и их виды
Треугольники и их виды Параллелограмм и его свойства
Параллелограмм и его свойства