Содержание
- 2. 1. Теоретическая разминка. 2. Тест. 3. Практикум. 4. Историческая справка. 5. Презентация специальных методов решения квадратных
- 3. Термин «квадратное уравнение» впервые ввёл Кристиан Вольф Кристиан Вольф - знаменитый немецкий философ. Родился в 1679
- 4. Английский математик, который ввёл термин «дискриминант». Сильвестр Джеймс Джозеф
- 5. В 13 – 16 веках даются отдельные методы решения различных видов квадратных уравнений. Слияние этих методов
- 6. Уравнение какого вида называют квадратным? Как по названиям различают коэффициенты а, в и с? Объясните, в
- 7. Неполные квадратные уравнения
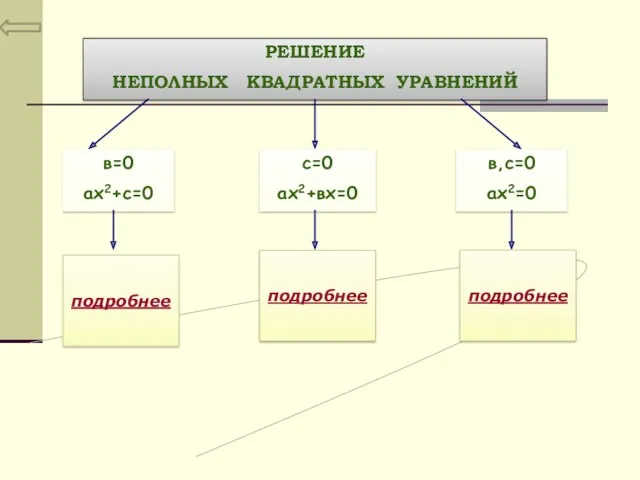
- 8. РЕШЕНИЕ НЕПОЛНЫХ КВАДРАТНЫХ УРАВНЕНИЙ в=0 ах2+с=0 с=0 ах2+вх=0 в,с=0 ах2=0 подробнее подробнее подробнее
- 9. Алгоритм решения 1.Переносим с в правую часть уравнения. ах2 = -с. 2. Делим обе части уравнения
- 10. Выносим x за скобки: х (ах + в) = 0. 2. «Разбиваем» уравнение на два: x
- 11. 1. Делим обе части уравнения на а≠0. х2 = 0 2. Одно решение: х = 0.
- 12. D Корней нет D = 0 D > 0
- 13. b = 2k (четное число)
- 14. Специальные методы Метод выделения квадрата двучлена Метод «переброски» старшего коэффициента На основании теорем
- 15. Цель: привести квадратное уравнение общего вида к неполному квадратному уравнению. Пример: Метод выделения квадрата двучлена Х2
- 16. Метод выделения квадрата двучлена (a + b)2 = a2 + 2ab + b2, (a - b)2
- 17. Корни квадратных уравнений и связаны соотношениями и В некоторых случаях бывает удобно решать сначала не данное
- 18. Метод “переброски” старшего коэффициента ax2 + bx + c = 0 и y2+ by + ac
- 19. На основании теорем: 1. Если в квадратном уравнении a+b+c=0, то один из корней равен 1, а
- 20. Теорема 1. Если в квадратном уравнении a + b + c = 0, то один из
- 21. Теорема 2. Если в квадратном уравнении a + c = b, то один из корней равен
- 22. Общие методы Разложение на множители; Введение новой переменной; Графический метод.
- 23. Метод разложения на множители привести квадратное уравнение общего вида к виду А(х)·В(х)=0, где А(х) и В(х)
- 24. Решите уравнение 4х2 + 5х + 1 = 0. 4х2 + 5х + 1 = 0.
- 25. Введение новой переменной. Умение удачно ввести новую переменную – важный элемент математической культуры. Удачный выбор новой
- 26. Метод введения новой переменной Решите уравнение (2х+3)2 = 3(2х+3) – 2. (2х+3)2 = 3(2х+3) – 2.
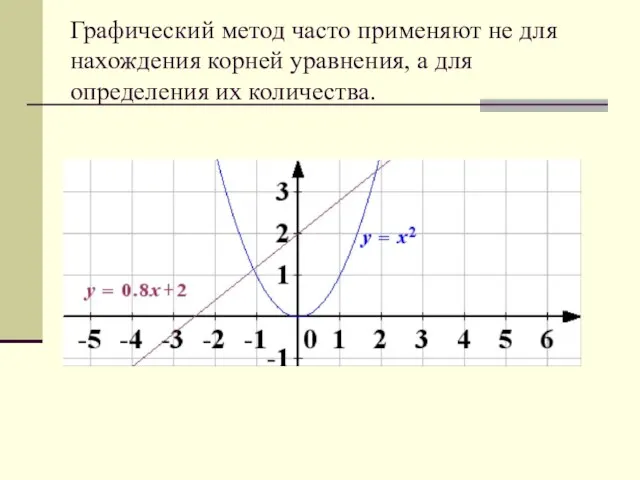
- 27. Графический метод Для решения уравнения f(x) = g(x) необходимо построить графики функций y = f(x), y
- 28. Графический метод часто применяют не для нахождения корней уравнения, а для определения их количества.
- 29. Практикум
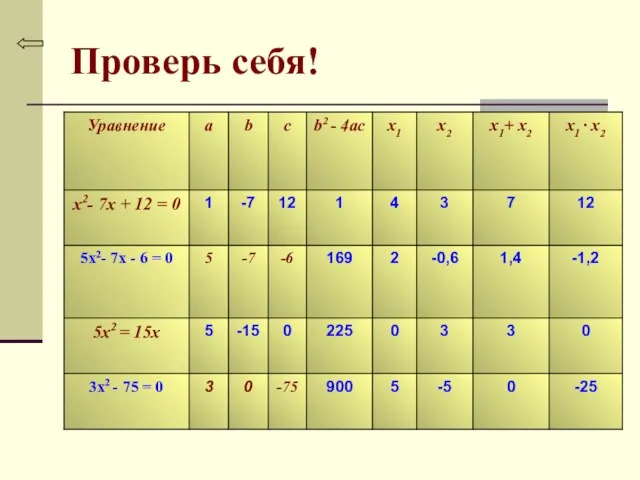
- 30. Проверь себя!
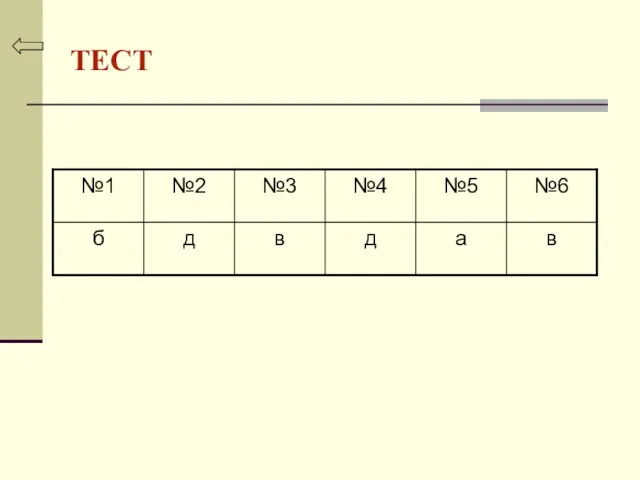
- 31. ТЕСТ
- 33. Скачать презентацию










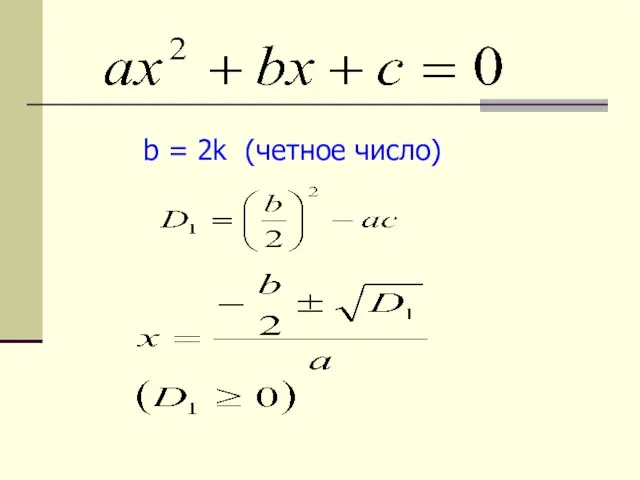















 Линейная алгебра. Матрицы и операции над ними
Линейная алгебра. Матрицы и операции над ними Формулы приведения
Формулы приведения Положительные и отрицательные числа. Модуль числа. Сравнение рациональных чисел
Положительные и отрицательные числа. Модуль числа. Сравнение рациональных чисел Сравнение дробей
Сравнение дробей Решение задач с помощью уравнений
Решение задач с помощью уравнений Круг. Окружность. Длина окружности. Площадь круга. 6 класс
Круг. Окружность. Длина окружности. Площадь круга. 6 класс Прямоугольный параллелепипед. К уроку изучения нового материала по математике в 5 классе
Прямоугольный параллелепипед. К уроку изучения нового материала по математике в 5 классе Решение банковских задач в новой версии ЕГЭ 2015 по математике
Решение банковских задач в новой версии ЕГЭ 2015 по математике Умножение и деление обыкновенной дроби на натуральное число. (Урок 72)
Умножение и деление обыкновенной дроби на натуральное число. (Урок 72) Метод алгебраического сложения. Алгоритм решения системы уравнений методом алгебраического сложения
Метод алгебраического сложения. Алгоритм решения системы уравнений методом алгебраического сложения Деление с остатком (5 класс)
Деление с остатком (5 класс) Вспоминаем, повторяем
Вспоминаем, повторяем Геометрический смысл производной
Геометрический смысл производной Путешествие в Африку! - презентация
Путешествие в Африку! - презентация Длина. Дециметр
Длина. Дециметр Математическое кафе. Открытый урок по математике в 5 классе
Математическое кафе. Открытый урок по математике в 5 классе Модуль геометрия. ОГЭ в 9 классе
Модуль геометрия. ОГЭ в 9 классе Отрицательные целые числа
Отрицательные целые числа Применение производной в физике
Применение производной в физике Умножение и деление обыкновенных дробей
Умножение и деление обыкновенных дробей Понятие движения в геометрии
Понятие движения в геометрии Тригонометрия. Единичная окружность. Определение синуса и косинуса угла. Тригонометрические тождества и формулы
Тригонометрия. Единичная окружность. Определение синуса и косинуса угла. Тригонометрические тождества и формулы Квадратичная функция
Квадратичная функция Оценка точности при параметрическом способе уравнивания
Оценка точности при параметрическом способе уравнивания Свойства корня n-й степени
Свойства корня n-й степени урок математики 4 класс Закрепление. Решение задач презентация
урок математики 4 класс Закрепление. Решение задач презентация Сравнение, сложение и вычитание десятичных дробей
Сравнение, сложение и вычитание десятичных дробей Случаи вычитания 12 -, 13 -
Случаи вычитания 12 -, 13 -