Содержание
- 2. Основные понятия Рассмотрим систему трёх линейных уравнений с тремя неизвестными: где - неизвестные, - коэффициенты (
- 3. Метод Крамера Пусть нам требуется решить систему трёх линейных уравнений с тремя неизвестными: (1) в которой
- 4. Решите систему методом Крамера: Решение: Вычислим определитель системы: Так как определитель системы отличен от нуля, то
- 5. Решите систему методом Крамера: Находим неизвестные по формулам Крамера: Ответ:
- 6. Метод Гаусса Ранее рассмотренный метод можно применять при решении только тех систем, в которых число уравнений
- 7. Метод Гаусса Теперь из последнего уравнения исключим слагаемое, содержащее x2. Для этого третье уравнение разделим на
- 8. Решите систему методом Гаусса: Решение: Первое уравнение оставим без изменения, а из 2-го и 3-го исключим
- 9. Решите систему методом Гаусса: На этом прямой ход метода Гаусса закончен, начинаем обратный ход. Из последнего
- 10. Матричный метод (с помощью обратной матрицы) Рассмотрим систему трёх линейных уравнений с тремя неизвестными: В матричной
- 11. Решите систему матричным методом: Решение: Перепишем систему уравнений в матричной форме: Так как то систему трёх
- 12. Решите систему матричным методом: Построим обратную матрицу с помощью матрицы из алгебраических дополнений элементов матрицы :
- 14. Скачать презентацию











 Модели числового неравенства. Числовые промежутки
Модели числового неравенства. Числовые промежутки Специфика преподавания математики в рамках УМК А.Г. Модковича. 10 - 11 классы
Специфика преподавания математики в рамках УМК А.Г. Модковича. 10 - 11 классы Математический диктант
Математический диктант Числовые неравенства и их свойства
Числовые неравенства и их свойства Длина ломаной
Длина ломаной Умники и умницы. Матиматека
Умники и умницы. Матиматека Графическое решение уравнений с двумя переменными
Графическое решение уравнений с двумя переменными Использование свойств функций при решении уравнений и неравенств
Использование свойств функций при решении уравнений и неравенств Вписанная и описанная окружности
Вписанная и описанная окружности Теорема Менелая
Теорема Менелая Действия с дробями
Действия с дробями Название чисел в записи действий. Закрепление.
Название чисел в записи действий. Закрепление. Геометрические тела
Геометрические тела Контурные интегралы функций комплексного переменного (ФКП)
Контурные интегралы функций комплексного переменного (ФКП) Линейные уравнения с двумя переменными
Линейные уравнения с двумя переменными Математика - царица наук
Математика - царица наук Презентация к уроку математики во 2 классе по теме Периметр
Презентация к уроку математики во 2 классе по теме Периметр Параллельность прямых и плоскостей в пространстве
Параллельность прямых и плоскостей в пространстве Возрастание и убывание функции. Применение производной к исследованию функций
Возрастание и убывание функции. Применение производной к исследованию функций Математика. Приклади. Диск
Математика. Приклади. Диск Графики тригонометрических функций и их свойства
Графики тригонометрических функций и их свойства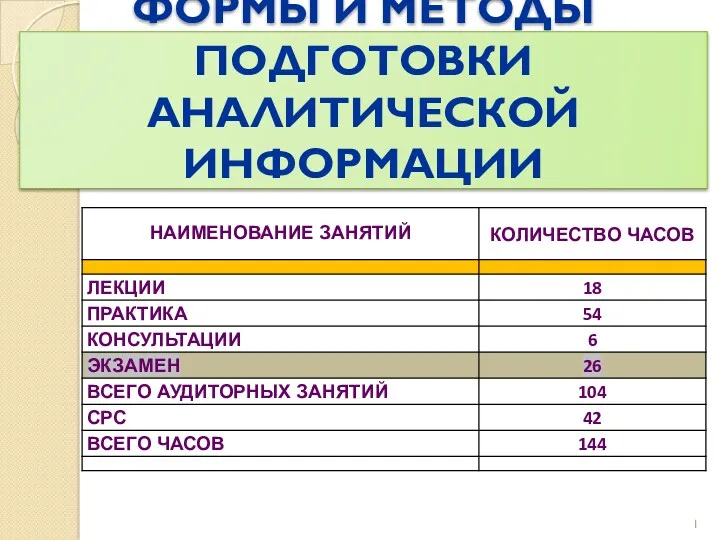 Формы и методы подготовки аналитической информации
Формы и методы подготовки аналитической информации Векторы в жизни
Векторы в жизни Математика в профессии электрика
Математика в профессии электрика Цилиндр. Цилиндрическая поверхность. Площадь полной поверхности и объем цилиндра
Цилиндр. Цилиндрическая поверхность. Площадь полной поверхности и объем цилиндра Первый урок алгебры в 7 классе
Первый урок алгебры в 7 классе Призма
Призма Время. Сутки
Время. Сутки