Содержание
- 2. ОСНОВНЫЕ ПОНЯТИЯ
- 3. Определение модели Простая линейная регрессия — это модель, описывающая зависимость величины y от одной переменной x
- 4. Спецификация модели Система уравнений − описание моделью выборочных данных (x1; y1),(x2 ; y2 ),...,(xn ; yn
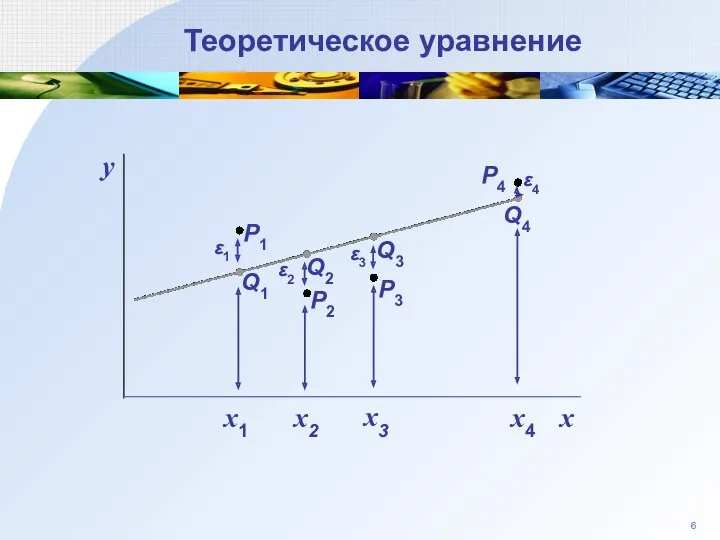
- 5. Теоретическое уравнение модели Сериальная ошибка — это разность между имеющимся значением зависимой переменной и соответствующим ему
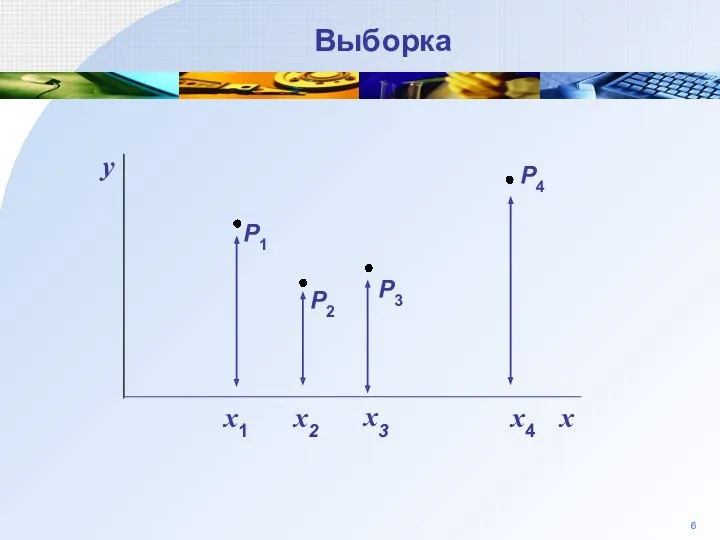
- 6. 6 Выборка P3 P2 P1 y P4
- 7. 6 Теоретическое уравнение P3 P2 P1 Q1 Q2 Q3 ε1 y ε2 ε3 Q4 P4 ε4
- 8. Теоретические ограничения У каждой сериальной ошибки математическое ожидание равно нулю Дисперсии всех сериальных ошибок одинаковы (гомоскедастичность
- 9. Теоретические ограничения Нормальная регрессия Параметрическая или нормальная или гауссовская регрессия − все сериальные ошибки имеют нормальное
- 10. Метод наименьших квадратов Задача о поиске теоретического уравнения не разрешима Найти a и b такие, что
- 11. Эмпирическое уравнение модели Эмпирическое уравнение модели − такое уравнение, у которого на имеющейся выборке сумма квадратов
- 12. Выровненные значения и остатки Выровненное значение − значение зависимой переменной, предсказанное с помощью эмпирического уравнения модели
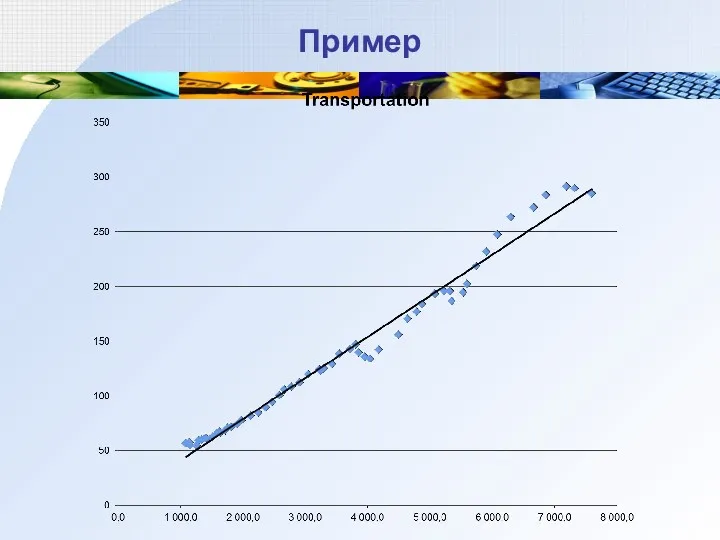
- 13. Пример Зависимость расходов на транспорт от дохода (США, 1946-2002 годы) Transp – совокупные расходы на транспорт
- 14. Пример
- 15. Пример Зависимость расходов на транспорт от дохода (США, 1946-2002 годы) Уравнение модели Transp –расходы на транспорт
- 16. Интрерпретация уравнения модели Зависимость расходов на транспорт от дохода (США, 1946-2002 годы) Коэффициент при DPI: если
- 17. Интрерпретация уравнения модели Коэффициент при объясняющей переменной: показывает, на сколько единиц примерно изменяется зависимая переменная при
- 18. ТЕОРЕМА О СУММЕ КВАДРАТОВ
- 19. Суммы квадратов Остатки: Любой анализ качества модели − это анализ остатков Полная сумма квадратов (total sum
- 20. Теорема о сумме квадратов Если в модели простой регрессии выполняются все теоретические предположения, то верно равенство:
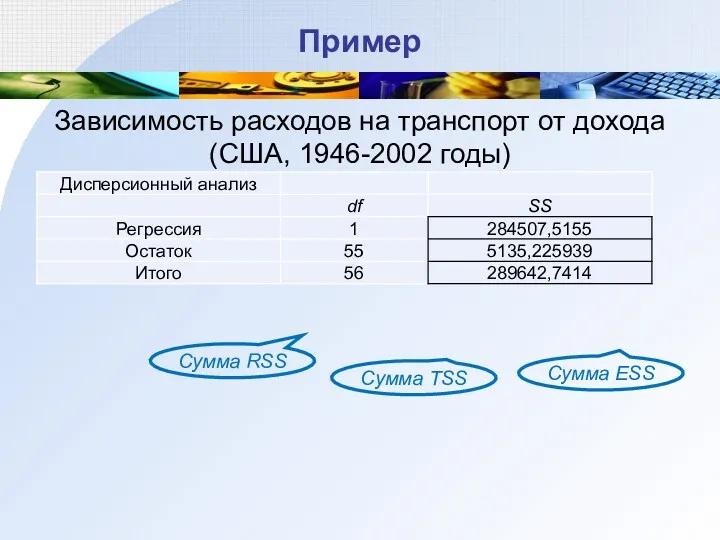
- 21. Пример Зависимость расходов на транспорт от дохода (США, 1946-2002 годы) Сумма ESS Сумма TSS Сумма RSS
- 22. Значимость модели Модель является значимой, если в теоретическом уравнении модели коэффициент при существенном факторе не равен
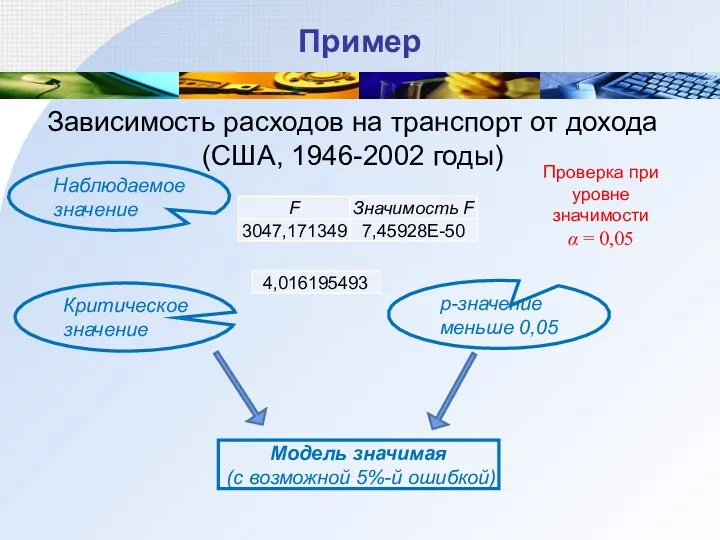
- 23. Проверка значимости модели Тест Фишера Основная гипотеза – модель незначимая Альтернативная – модель значимая Наблюдаемое значение:
- 24. Пример Зависимость расходов на транспорт от дохода (США, 1946-2002 годы) Наблюдаемое значение Критическое значение Модель значимая
- 25. Коэффициент детерминации Коэффициент детерминации: Выводы о качестве модели Коэффициент меньше примерно 0,2: модель плохо описывает имеющиеся
- 26. Пример Зависимость расходов на транспорт от дохода (США, 1946-2002 годы) Модель качественная
- 27. СТАНДАРТНЫЕ ОШИБКИ
- 28. Стандартная ошибка модели Стандартная ошибка модели – несмещенная оценка среднего квадратического отклонения сериальных ошибок Формула вычисления:
- 29. Пример Зависимость расходов на транспорт от дохода (США, 1946-2002 годы) Стандартная ошибка модели
- 30. Стандартные ошибки параметров Стандартная ошибка параметра a – несмещенная оценка среднего квадратического отклонения случайной величины â
- 31. Стандартные ошибки параметров Стандартная ошибка параметра b – несмещенная оценка среднего квадратического отклонения случайной величины Формула
- 32. Пример Зависимость расходов на транспорт от дохода (США, 1946-2002 годы) Стандартная ошибка свободного члена Стандартная ошибка
- 33. Интервальные оценки Интервальная оценка параметра: показывает с вероятностью 1– α , в каком интервале содержится истинное
- 34. Интервальные оценки Интервальная оценка свободного члена: нижняя граница интервала верхняя граница интервала – точечная оценка свободного
- 35. Интервальные оценки Интервальная оценка углового коэффициента: нижняя граница интервала верхняя граница интервала – точечная оценка углового
- 36. Пример Зависимость расходов на транспорт от дохода (США, 1946-2002 годы) Интервальная оценка свободного члена Интервальная оценка
- 37. ЗНАЧИМОСТЬ ПАРАМЕТРОВ МОДЕЛИ
- 38. Определения Параметр при существенном факторе x называется значимым, если его истинное значение не равно нулю Значимость
- 39. Значимость модели и параметров В модели простой линейной регрессии значимость параметра при существенном факторе равносильна значимости
- 40. Проверка значимости параметра Тест Стьюдента Основная гипотеза – параметр b незначимый Альтернативная – параметр b значимый
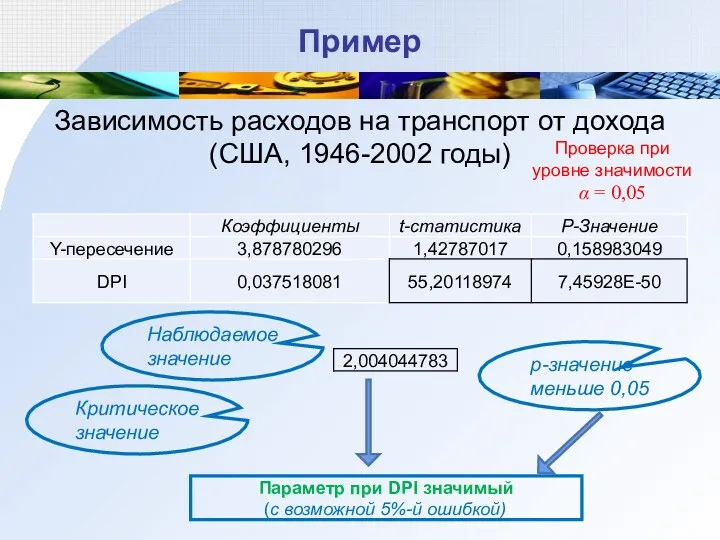
- 41. Пример Зависимость расходов на транспорт от дохода (США, 1946-2002 годы) Параметр при DPI значимый (с возможной
- 42. ПРОГНОЗИРОВАНИЕ
- 43. Виды прогнозирования Безусловное прогнозирование (предсказание): значение существенного фактора, соответствующее прогнозируемому значению, известно Условное прогнозирование: значение существенного
- 44. Точечный прогноз Точечный прогноз: значение зависимой переменной, вычисленное с помощью эмпирического уравнения модели Вычисление: x0 –
- 45. Стандартная ошибка Стандартная ошибка точечного прогноза: несмещенная оценка стандартного отклонения случайной величины Вычисление: s – стандартная
- 46. Интервальный прогноз Интервальная прогноз: показывает с вероятностью 1– α , в каком интервале содержится истинное значение
- 47. Интервальный прогноз Вычисление: нижняя граница интервала верхняя граница интервала – точечный прогноз – стандартная ошибка прогноза
- 48. Пример Зависимость расходов на транспорт от дохода (США, 1946-2002 годы)
- 49. НЕЛИНЕЙНАЯ РЕГРЕССИЯ
- 50. Нелинейные модели Два вида регрессий: нелинейные относительно объясняющих переменных, но линейные по оцениваемым параметрам нелинейные по
- 51. Пример Кривые Энгеля показывает зависимость между объёмом потребления товаров или услуг и доходом потребителя при неизменных
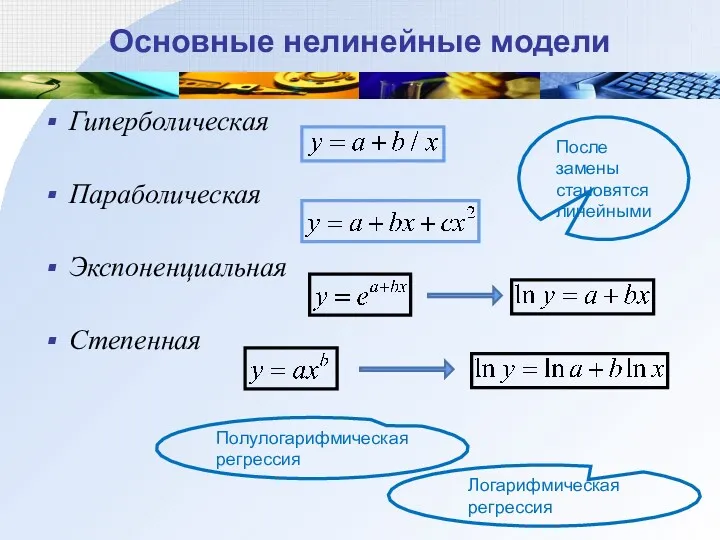
- 52. Основные нелинейные модели Гиперболическая Параболическая Экспоненциальная Степенная После замены становятся линейными Полулогарифмическая регрессия Логарифмическая регрессия
- 53. ВЫБОР ЛУЧШЕЙ МОДЕЛИ
- 54. Оценка качества модели Инструменты Точечная диаграмма (расположение точек вдоль линии тренда) Статистика Фишера (значимость модели по
- 55. Оценка качества модели Характеристики подходящей модели На диаграмме точки расположены, в основном, вдоль линии тренда Модель
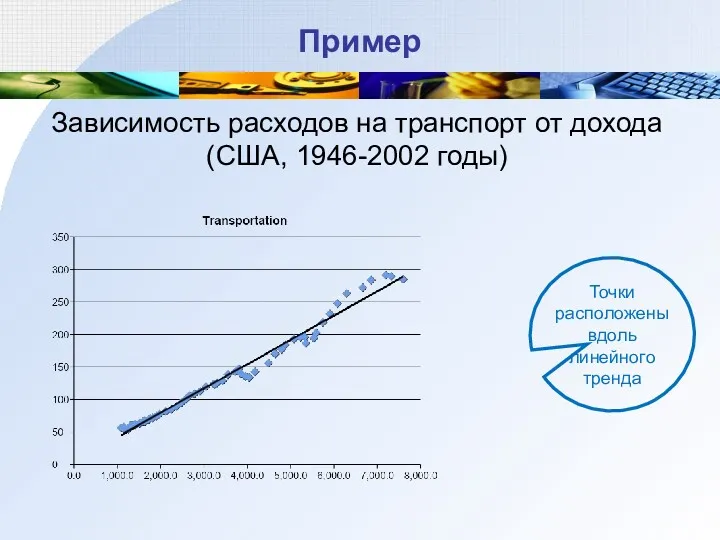
- 56. Пример Зависимость расходов на транспорт от дохода (США, 1946-2002 годы) Точки расположены вдоль линейного тренда
- 57. Пример Зависимость расходов на транспорт от дохода (США, 1946-2002 годы) Статистика Фишера Коэффициент детерминации Средняя относительная
- 58. Выбор модели Два этапа Первый этап: выбор подходящих моделей Обычно используются: линейная, гиперболическая, параболическая, экспоненциальная, степенная
- 59. Выбор модели Два этапа Второй этап: выбор лучшей модели Для сравнения подходящих моделей используются такие же
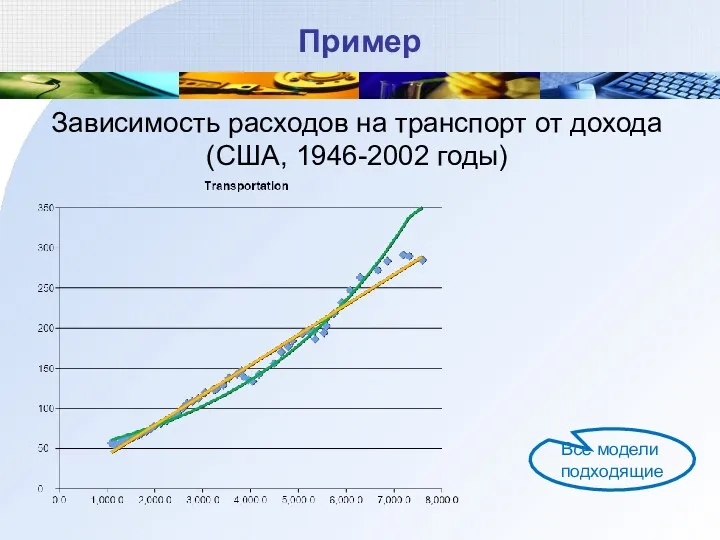
- 60. Пример Зависимость расходов на транспорт от дохода (США, 1946-2002 годы) Все модели подходящие
- 62. Скачать презентацию


















































 Стандартный вид числа
Стандартный вид числа Arvutusülesanded ühe osaleva aine järgi
Arvutusülesanded ühe osaleva aine järgi Определенный интеграл
Определенный интеграл Применение ИКТ для повышения качества образования
Применение ИКТ для повышения качества образования Треугольники. Основные признаки и свойства треугольников
Треугольники. Основные признаки и свойства треугольников Сравнение дробей
Сравнение дробей Арифметическая и геометрическая прогрессии. Обобщающий урок
Арифметическая и геометрическая прогрессии. Обобщающий урок Открытый урок по математике в 4 классе по УМК Гармония по теме Действия с величинами. Соотношения единиц длины.
Открытый урок по математике в 4 классе по УМК Гармония по теме Действия с величинами. Соотношения единиц длины. Виды треугольников. 3 класс
Виды треугольников. 3 класс Среднее арифметическое
Среднее арифметическое Подготовка к ЕГЭ
Подготовка к ЕГЭ Применение ИКТ на уроках математики, как средство формирования УУД у школьников
Применение ИКТ на уроках математики, как средство формирования УУД у школьников Парная регрессия и корреляция
Парная регрессия и корреляция Делимость натуральных чисел
Делимость натуральных чисел Решение простых задач на увеличение и уменьшение
Решение простых задач на увеличение и уменьшение Многоугольники
Многоугольники Выборочное наблюдение
Выборочное наблюдение Задачи на готовых чертежах
Задачи на готовых чертежах Угол. Измерение углов. Виды углов
Угол. Измерение углов. Виды углов Сравнение чисел
Сравнение чисел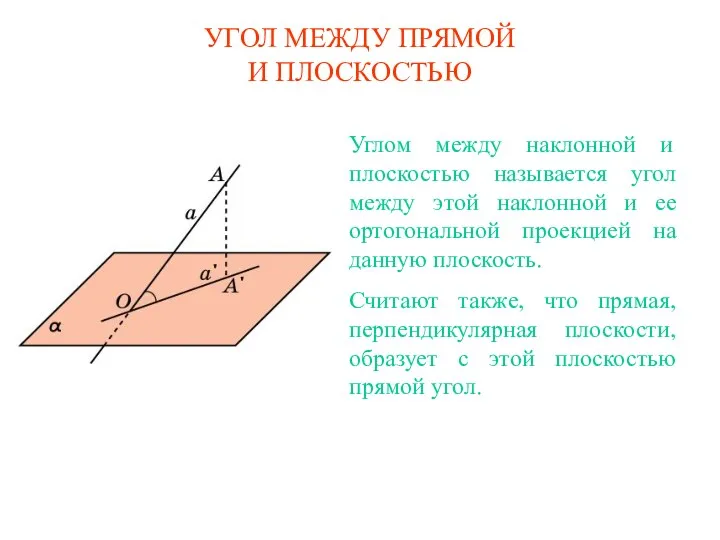 5.Угол между прямой и плоскостью (куб), задачи
5.Угол между прямой и плоскостью (куб), задачи Презентация Геометрическое ассорти Диск
Презентация Геометрическое ассорти Диск Решение задач и выражений. Таблица сложения. Закрепление вычислительных навыков
Решение задач и выражений. Таблица сложения. Закрепление вычислительных навыков Из истории мер длины
Из истории мер длины Столбчатые диаграммы. 6 класс
Столбчатые диаграммы. 6 класс Задачи на нахождение неизвестного третьего слагаемого
Задачи на нахождение неизвестного третьего слагаемого Визначники матриць (продовження). Системи лінійних рівнянь
Визначники матриць (продовження). Системи лінійних рівнянь Колебания напряжения в бытовых электрических сетях
Колебания напряжения в бытовых электрических сетях