Содержание
- 2. Lecture Outline Graphs of transformed Exponential functions Graphs of transformed Logarithmic functions Mathematical modelling Exponential Growth
- 3. Mathematical models Modelling using Exponents and Logarithms Often data does not fit to a linear or
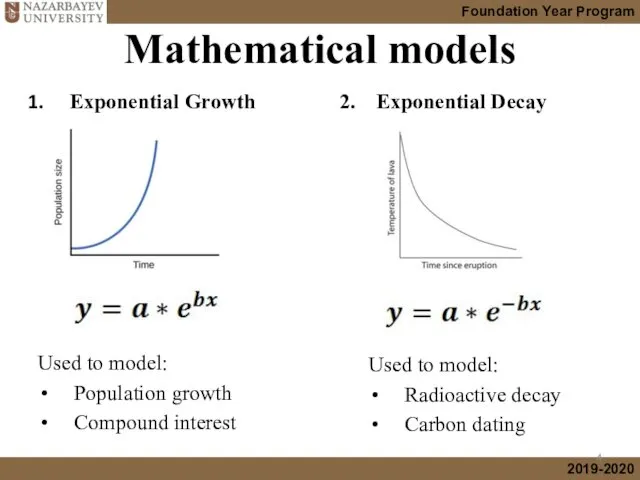
- 4. Mathematical models Exponential Growth Used to model: Population growth Compound interest 2. Exponential Decay Used to
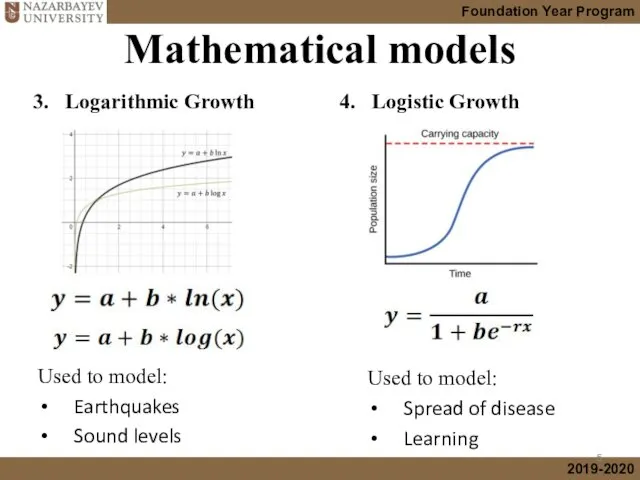
- 5. Mathematical models 3. Logarithmic Growth Used to model: Earthquakes Sound levels 4. Logistic Growth Used to
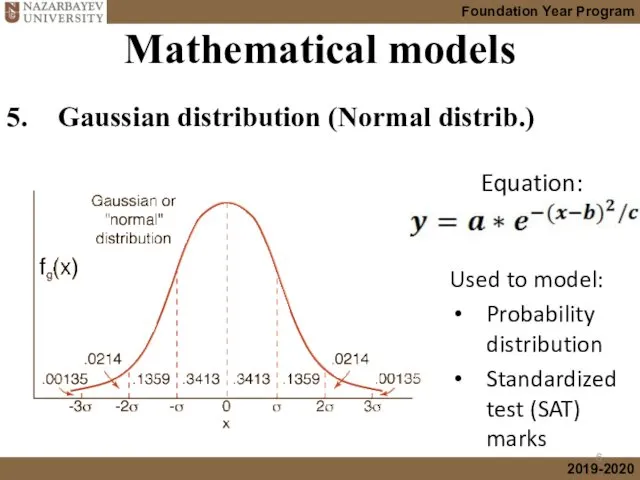
- 6. Mathematical models 5. Gaussian distribution (Normal distrib.) Used to model: Probability distribution Standardized test (SAT) marks
- 7. Mathematical models Exponential Growth Exponential Decay Logarithmic Model Logistic Growth Gaussian Distribution (Normal Distribution) Note: In
- 8. Introduction to “e” Mathematical constant e is a real, irrational and transcendental number approximately equal to:
- 9. “e” is almost everywhere The logarithmic spiral is a shape that appears in nature, and is
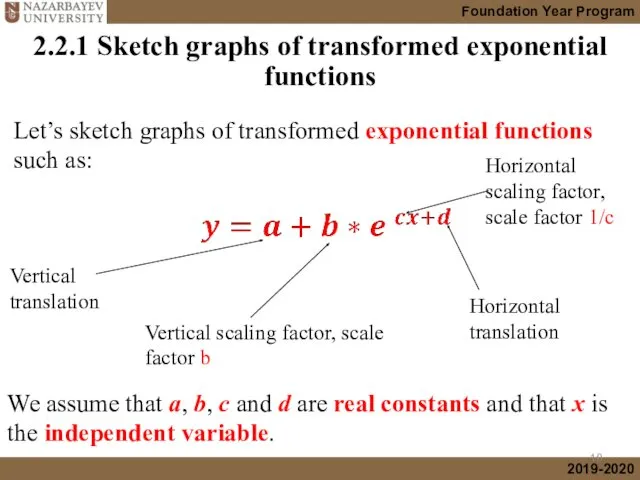
- 10. 2.2.1 Sketch graphs of transformed exponential functions Vertical translation Vertical scaling factor, scale factor b Horizontal
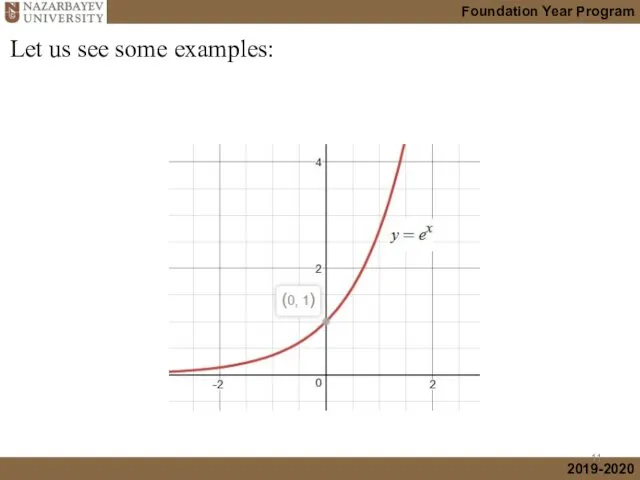
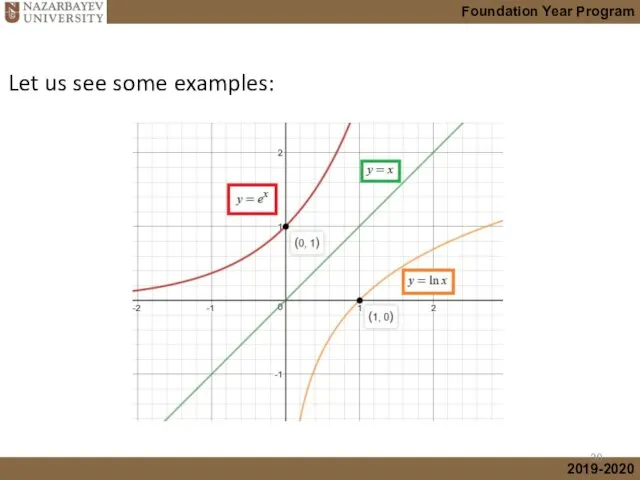
- 11. Let us see some examples:
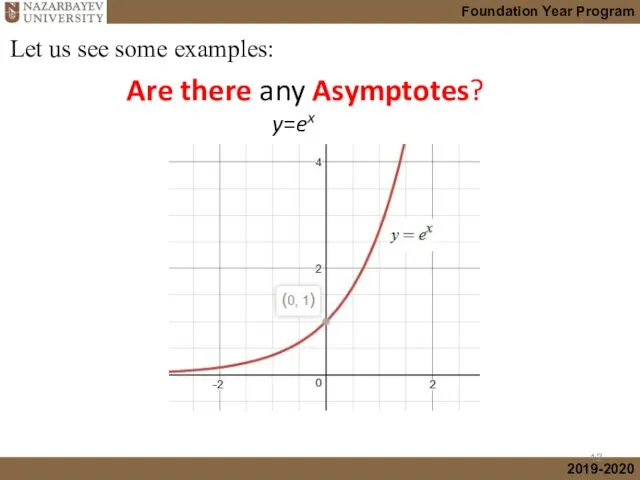
- 12. Are there any Asymptotes? y=ex Let us see some examples:
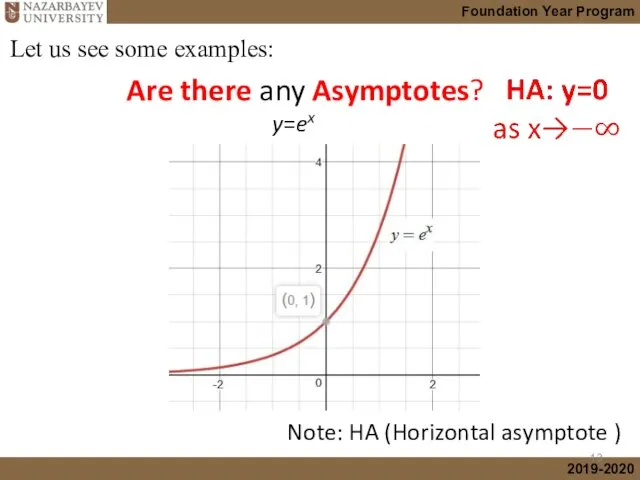
- 13. Are there any Asymptotes? y=ex Let us see some examples: Note: HA (Horizontal asymptote )
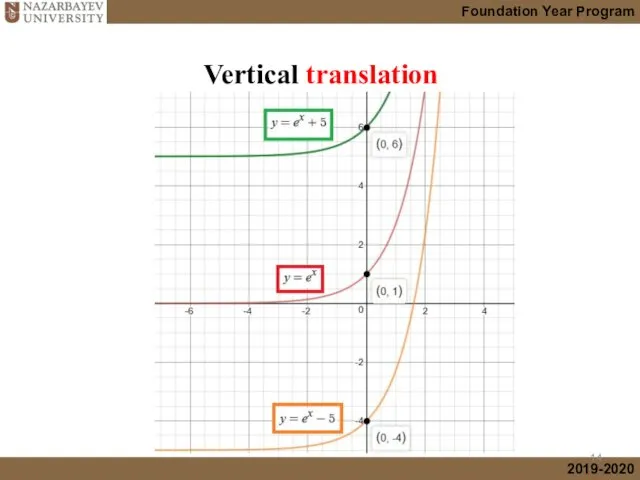
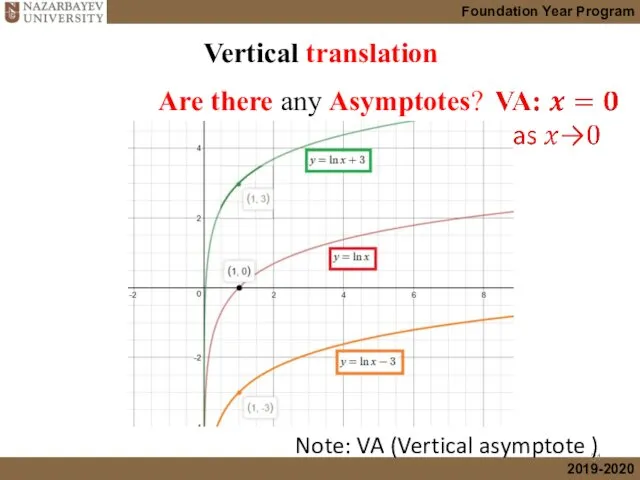
- 14. Vertical translation
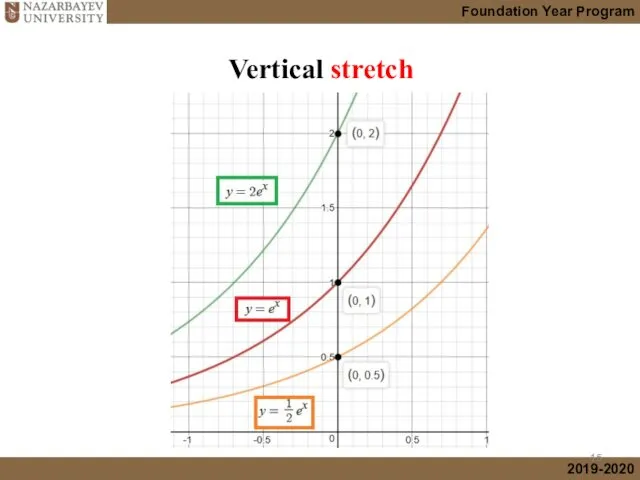
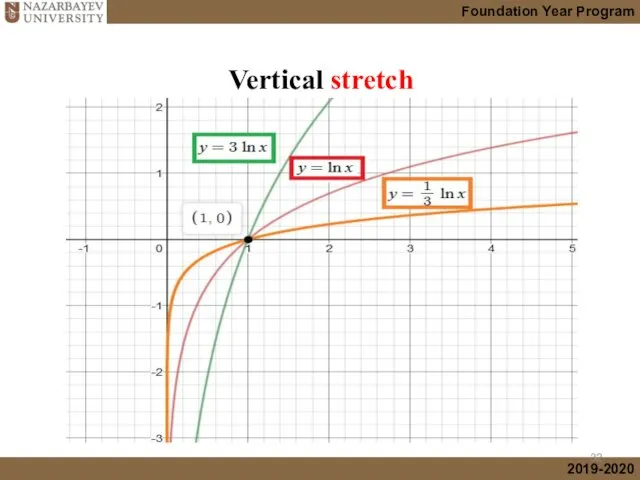
- 15. Vertical stretch
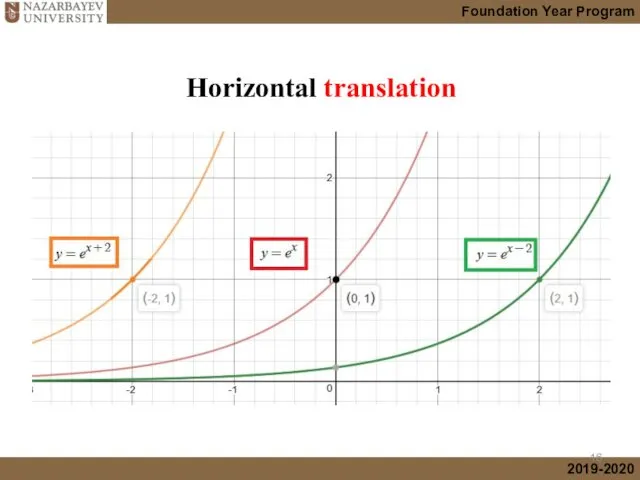
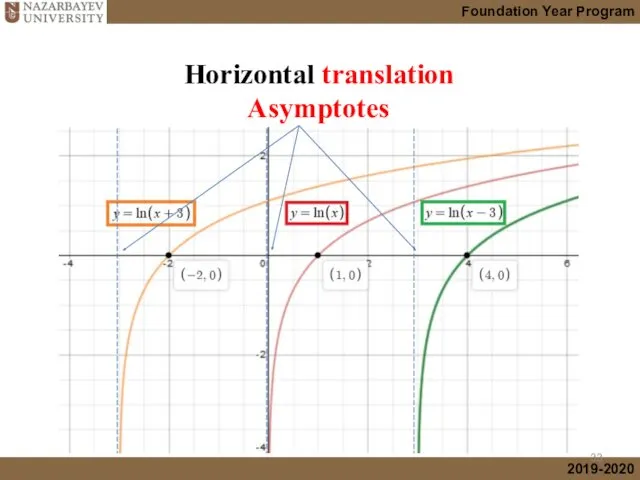
- 16. Horizontal translation
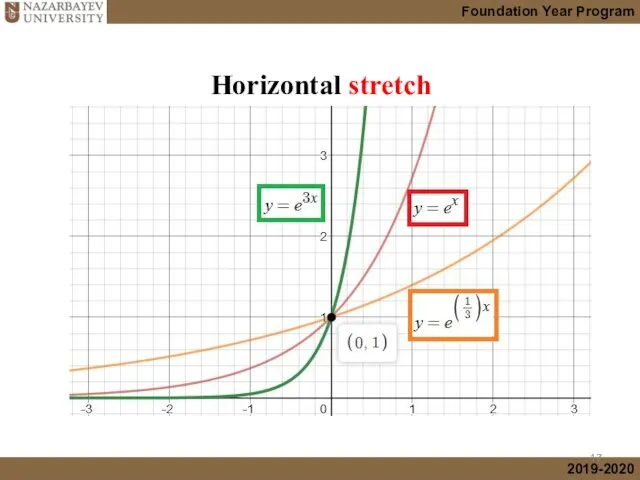
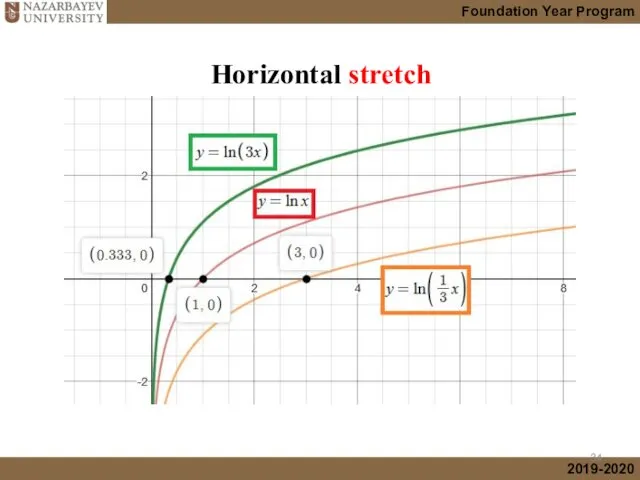
- 17. Horizontal stretch
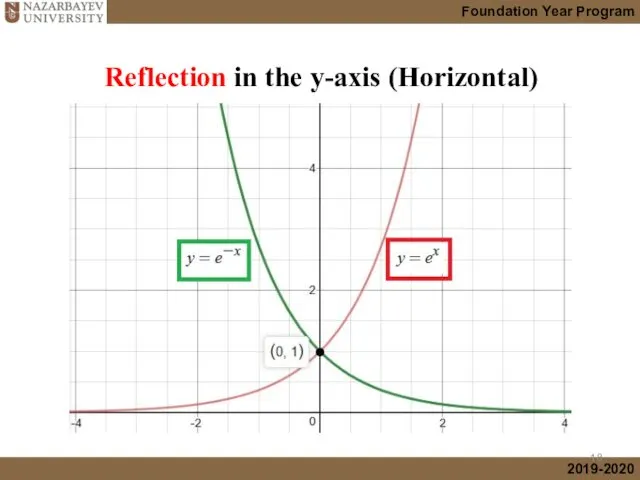
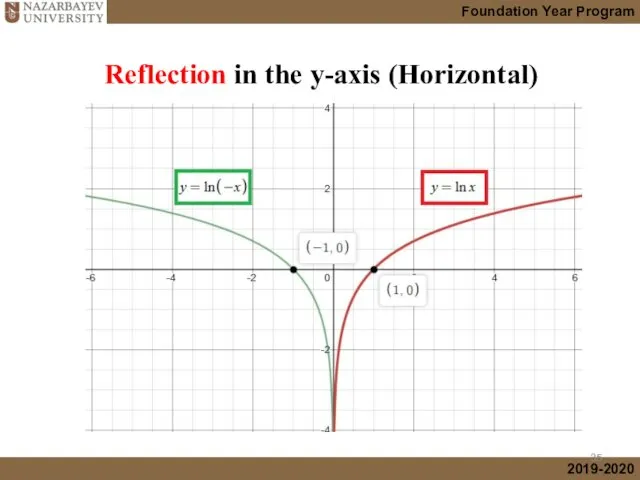
- 18. Reflection in the y-axis (Horizontal)
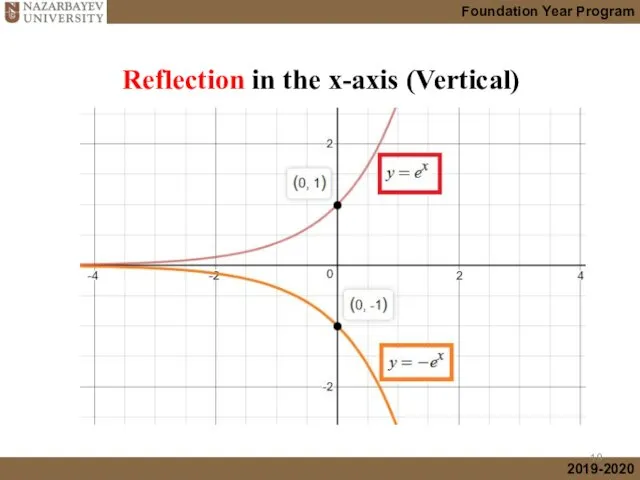
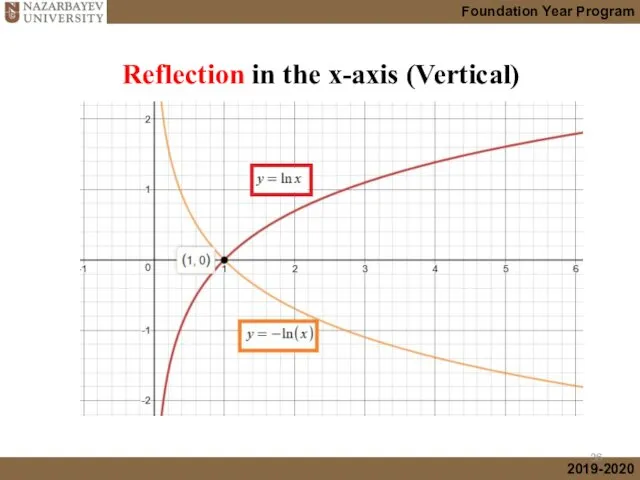
- 19. Reflection in the x-axis (Vertical)
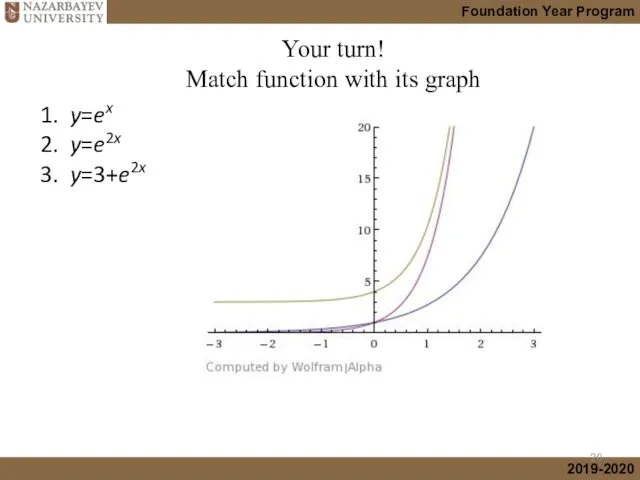
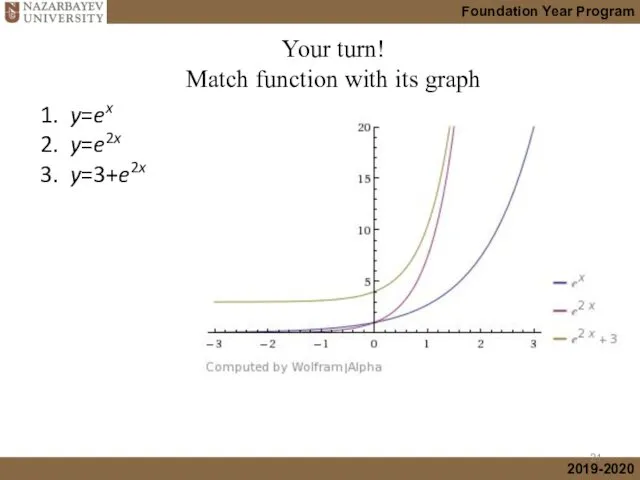
- 20. 1. y=ex 2. y=e2x 3. y=3+e2x (graphs with different scales) Your turn! Match function with its
- 21. 1. y=ex 2. y=e2x 3. y=3+e2x (graphs with different scales) Your turn! Match function with its
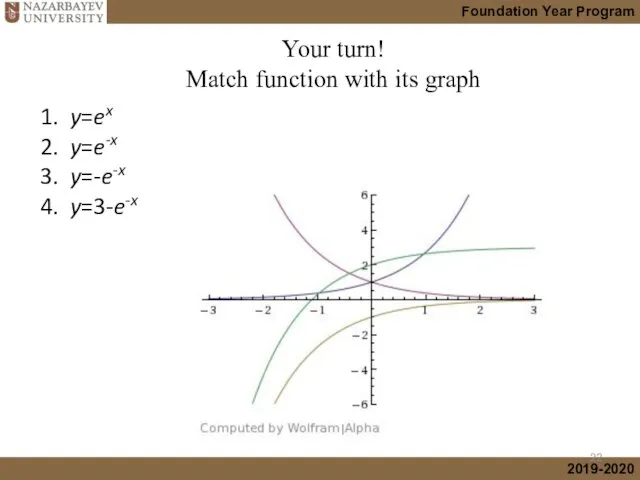
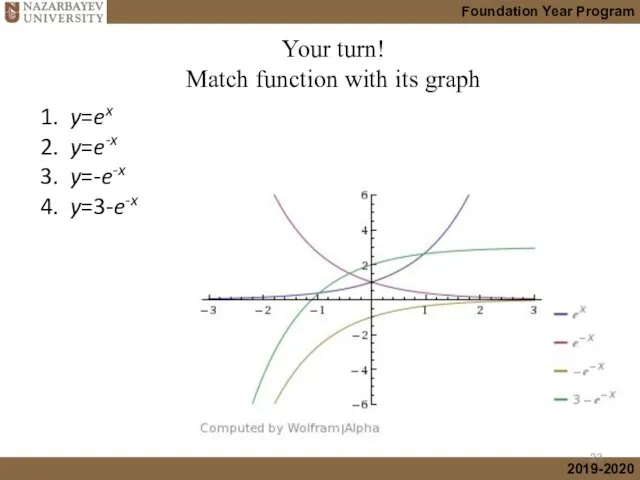
- 22. 1. y=ex 2. y=e-x 3. y=-e-x 4. y=3-e-x Your turn! Match function with its graph
- 23. 1. y=ex 2. y=e-x 3. y=-e-x 4. y=3-e-x Your turn! Match function with its graph
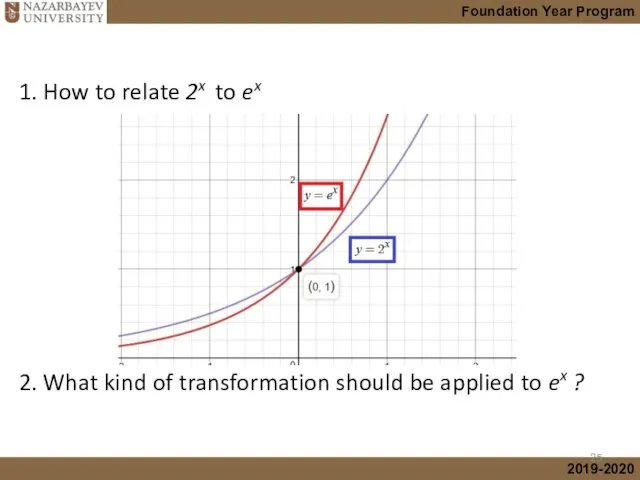
- 24. Have you noticed that we are now dealing with only base “e”? What is the reason
- 25. 1. How to relate 2x to ex 2. What kind of transformation should be applied to
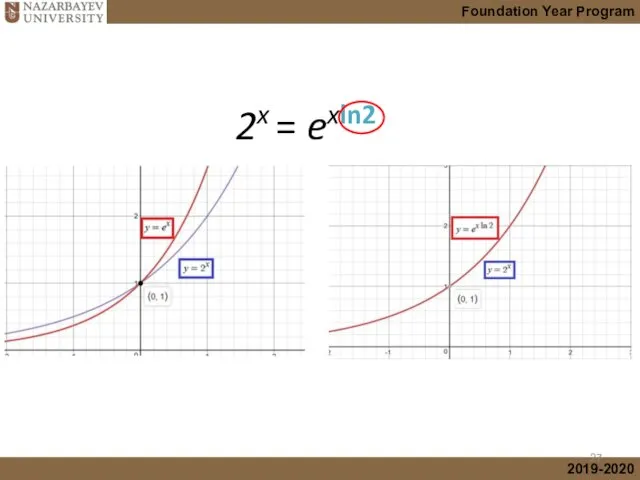
- 26. Answer: we need to apply horizontal stretch, i.e. and introduce a coefficient c 2x = ecx
- 27. 2x = exln2
- 28. That is why in Exponential growth and decay models we use directly “e” number that can
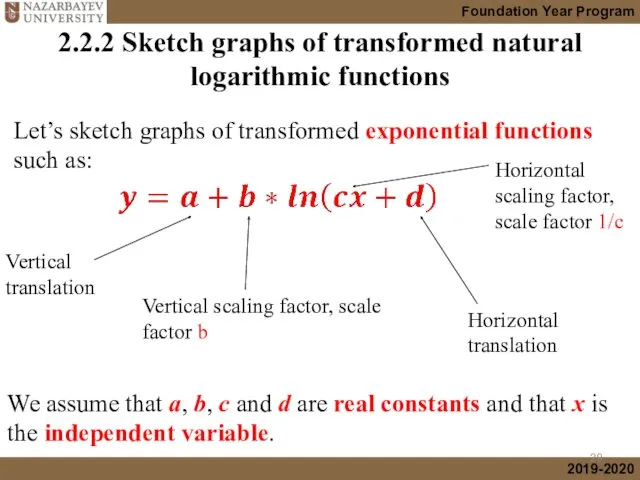
- 29. 2.2.2 Sketch graphs of transformed natural logarithmic functions Vertical translation Vertical scaling factor, scale factor b
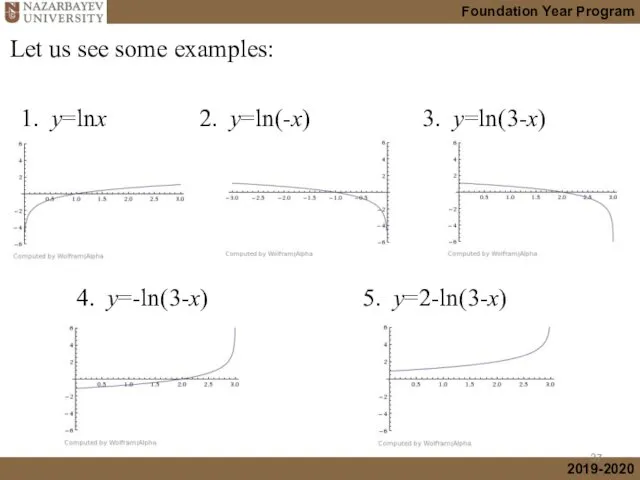
- 30. Let us see some examples:
- 31. Vertical translation Are there any Asymptotes? Note: VA (Vertical asymptote )
- 32. Vertical stretch
- 33. Horizontal translation Asymptotes
- 34. Horizontal stretch
- 35. Reflection in the y-axis (Horizontal)
- 36. Reflection in the x-axis (Vertical)
- 37. 1. y=lnx 2. y=ln(-x) 3. y=ln(3-x) 4. y=-ln(3-x) 5. y=2-ln(3-x) Let us see some examples:
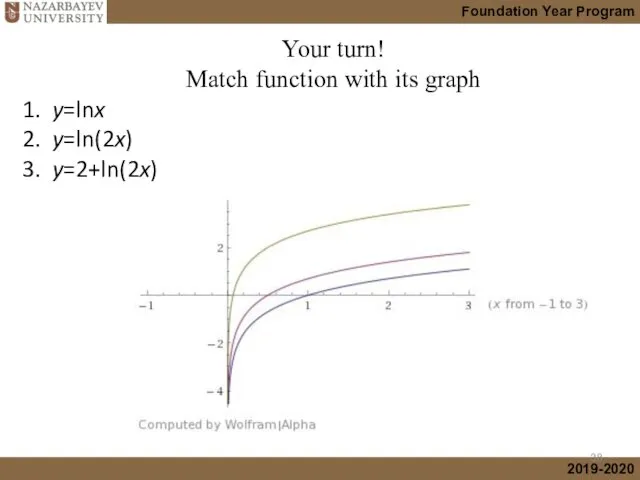
- 38. 1. y=lnx 2. y=ln(2x) 3. y=2+ln(2x) Your turn! Match function with its graph
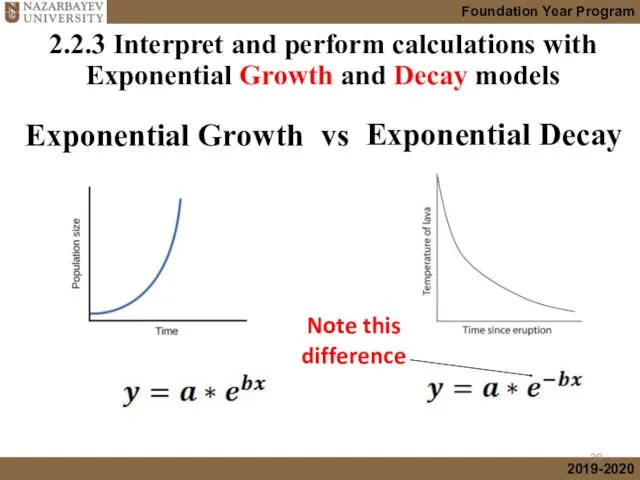
- 39. 2.2.3 Interpret and perform calculations with Exponential Growth and Decay models Exponential Growth Exponential Decay Note
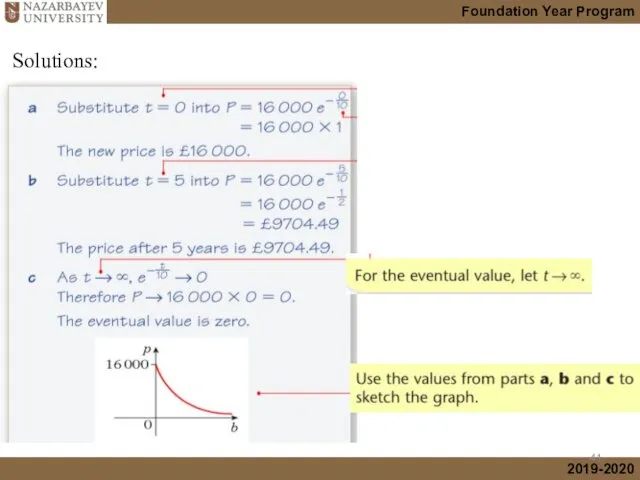
- 40. Example 1 Decay model The new price The value at 5 years old car What the
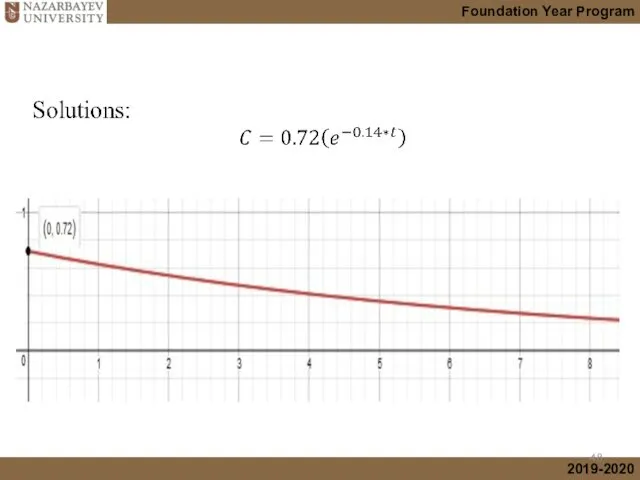
- 41. Solutions:
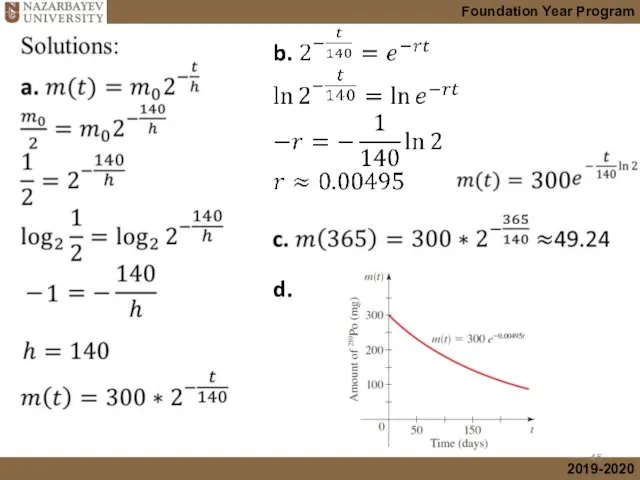
- 42. Your turn (Example 2 Growth model) The exponential growth of a colony of bacteria can modeled
- 43. a. Initial population A= 60e0.03(0)=60e0=60 bacteria Solutions: A=60e(0.03t) c. After what time t will the number
- 45. d.
- 49. 2.2.4 Solve applications involving Exponential and Logarithmic functions Example 5 (Law of forgetting)
- 50. Solutions:
- 51. Example 6 (Magnitude of earthquake)
- 52. Solutions:
- 53. Your turn (Example 7)
- 54. Solutions:
- 55. Learning outcomes At the end of this lecture, you should be able to: 2.2.1 Sketch the
- 56. Foundation Year Program Preview activity 1: Trigonometry Watch this video https://www.youtube.com/watch?v=T9lt6MZKLck
- 58. Скачать презентацию






















 Деление на десятичную дробь
Деление на десятичную дробь Вписанная и описанная окружности. Часть 1. 8 класс
Вписанная и описанная окружности. Часть 1. 8 класс Основные математические положения, применяемые для анализа и построения статистической модели
Основные математические положения, применяемые для анализа и построения статистической модели Сложение и вычитание одночленов
Сложение и вычитание одночленов Арифметические действия (повторение)
Арифметические действия (повторение) Методы кибернетики
Методы кибернетики Множества точек на координатной прямой
Множества точек на координатной прямой Математика в жизни моей семьи
Математика в жизни моей семьи По сказочной стране Геометрии (конспект с презентацией)
По сказочной стране Геометрии (конспект с презентацией) Нахождение дроби от числа
Нахождение дроби от числа Решение задач №19. Проценты
Решение задач №19. Проценты Тест по математике
Тест по математике Выпуклый анализ. Выпуклые множества. Лекция 5
Выпуклый анализ. Выпуклые множества. Лекция 5 Теріс сандарды қосу
Теріс сандарды қосу Тени. Общие положения. Чертежи пространственных фигур. (Лекция 12)
Тени. Общие положения. Чертежи пространственных фигур. (Лекция 12) Масштаб. Решение задач
Масштаб. Решение задач Математика в средневековой Индии
Математика в средневековой Индии Графический способ решения уравнений
Графический способ решения уравнений Знакомство с задачами
Знакомство с задачами Движение
Движение Весёлая математика. Задачи в стихах
Весёлая математика. Задачи в стихах сумма трёх и более слагаемых
сумма трёх и более слагаемых Прямые. Взаимное расположение прямых в пространстве. Признак скрещивающихся прямых
Прямые. Взаимное расположение прямых в пространстве. Признак скрещивающихся прямых Элементы стереометрии
Элементы стереометрии Предел функции в бесконечности
Предел функции в бесконечности Уменьшаемое, вычитаемое, разность
Уменьшаемое, вычитаемое, разность Случайные события. Вероятность события
Случайные события. Вероятность события Задачи на построение сечений. 10 класс
Задачи на построение сечений. 10 класс