Неопределенный интеграл. Основные свойства. Методы интегрирования. Первообразная функция. (Лекция 7) презентация
Содержание
- 2. Пусть f(x) определена на некотором множестве М, которое является конечным или бесконечным интервалом. Определение 1 F(x)
- 3. Определение 2 Совокупность всех первообразных функций для f(x) на множестве М называется неопределенным интегралом от функции
- 4. Основные свойства неопределенного интеграла Свойства вытекают из определения неопределенного интеграла Дифференциал неопределенного интеграла равен подынтегральному выражению,
- 5. 3. Отличный от нуля постоянный множитель можно выносить за знак интеграла. То есть, если , то
- 6. Таблица простейших неопределенных интегралов Имеем соотношения Обобщая формулы дифференцирования, получим
- 8. Независимость вида неопределенного интеграла от выбора аргумента Приведенная таблица полностью сохраняет свое значение, если под х
- 9. u – любая непрерывно дифференцируемая функция от независимой переменной. Выбирая различным образом функцию u можно существенно
- 10. 1) 2) 3) 4) 5) sinxdx=-d(cosx) 6) cosxdx=d(sinx) В общем случае f’(x)dx=d(f(x)) Примеры 1. 2. 3.
- 11. 4. 5. 6. 7. 8. 9.
- 12. Основные методы интегрирования Для вычисления данного интеграла необходимо тем или иным способом свести его к табличному
- 13. 3 (так как ) Пусть f(x) непрерывна на интервале (a,b) и непрерывно дифференцируема на интервале ;
- 14. 2 Выполним тригонометрическую подстановку x=asint, dx=acostdt Следовательно Делая обратную замену Окончательно Иногда формулу (1) полезно применять
- 15. 2. так как получаем Метод интегрирования по частям Пусть u и v – непрерывно дифференцируемые функции
- 16. Интегрирование рациональных дробей с квадратичным знаменателем Рассмотрим интеграл вида , где P(x) – целочисленный многочлен; a,b,c
- 17. Тогда III. К интегралам I и II присоединим еще один интеграл Примеры 1. 2. Замечание Основной
- 18. 4. 5. 6. Замечание Если выражение имеет действительные и различные корни, то для вычисления интеграла (1)
- 19. 1. Приравнивая коэффициенты, получаем систему уравнений На основании полученного разложения исходный интеграл Интегрирование иррациональностей Рассмотрим способы
- 20. . Рассмотрим эти интегралы: a) Применим подстановку Эйлера где t –новая переменная. отсюда Пример b) Пример
- 21. 3. Интеграл от иррациональности Заменой он сводится к интегралу вида 2). Действительно После всех замен получаем
- 22. Окончательно = Замечание a) b) При вычислении можно использовать гиперболические функции x=sht, dx=cht (можно x=tgt, но
- 24. Скачать презентацию









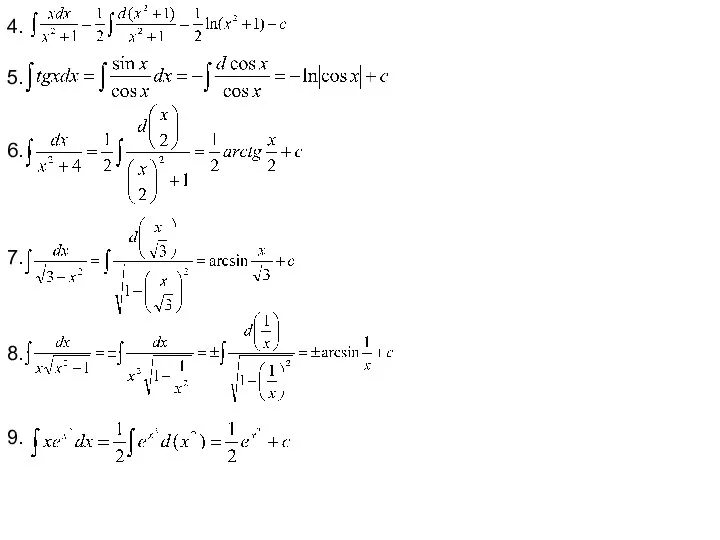











 Величины. Таблица единиц площади.
Величины. Таблица единиц площади. Обратные действия. Увеличение и уменьшение числа
Обратные действия. Увеличение и уменьшение числа Приближенные значения чисел. Округление чисел
Приближенные значения чисел. Округление чисел Площади плоских фигур и поверхности тел
Площади плоских фигур и поверхности тел Деление на группы по несколько предметов.
Деление на группы по несколько предметов. Умножение и деление на 3.
Умножение и деление на 3. Решение задач по теме Площади фигур
Решение задач по теме Площади фигур Свойства сложения натуральных чисел. Урок математики в 5 классе
Свойства сложения натуральных чисел. Урок математики в 5 классе Синус, косинус и тангенс угла
Синус, косинус и тангенс угла Роль и место математики в мире и медицине
Роль и место математики в мире и медицине Урок - сказка по математике
Урок - сказка по математике Волшебные часы
Волшебные часы Решение тригонометрических неравенств
Решение тригонометрических неравенств Развитие функционально-графического мышления учащихся при изучении алгебры 7-9 класс
Развитие функционально-графического мышления учащихся при изучении алгебры 7-9 класс Элементы математической статистики
Элементы математической статистики Геометрические фигуры.
Геометрические фигуры. Презентация практических достижений профессиональной деятельности по образовательной области Познавательное развитие
Презентация практических достижений профессиональной деятельности по образовательной области Познавательное развитие Неравенства и системы неравенств с двумя переменными
Неравенства и системы неравенств с двумя переменными Системы уравнений с несколькими неизвестными. Метод замены неизвестных
Системы уравнений с несколькими неизвестными. Метод замены неизвестных Логарифмы в природе
Логарифмы в природе Линейная алгебра
Линейная алгебра Системы уравнений с двумя переменными (9 класс)
Системы уравнений с двумя переменными (9 класс) Презентация по математике по теме Вычитание чисел 6,7,8,9. Освоение приема вида□ – 6; □ – 7; □ – 8; □ – 9.
Презентация по математике по теме Вычитание чисел 6,7,8,9. Освоение приема вида□ – 6; □ – 7; □ – 8; □ – 9. Презентация Занимательная математика
Презентация Занимательная математика Функція = + bx + c, її властивості та графік
Функція = + bx + c, її властивості та графік Математическая игра Думай, считай, отгадывай
Математическая игра Думай, считай, отгадывай Центральная и осевая симметрия
Центральная и осевая симметрия Построение графика квадратичной функции
Построение графика квадратичной функции