Содержание
- 2. Объем пирамиды.
- 3. Научиться применять интегрирование функций в качестве одного из способов решения задач на нахождение объёмов геометрических тел.
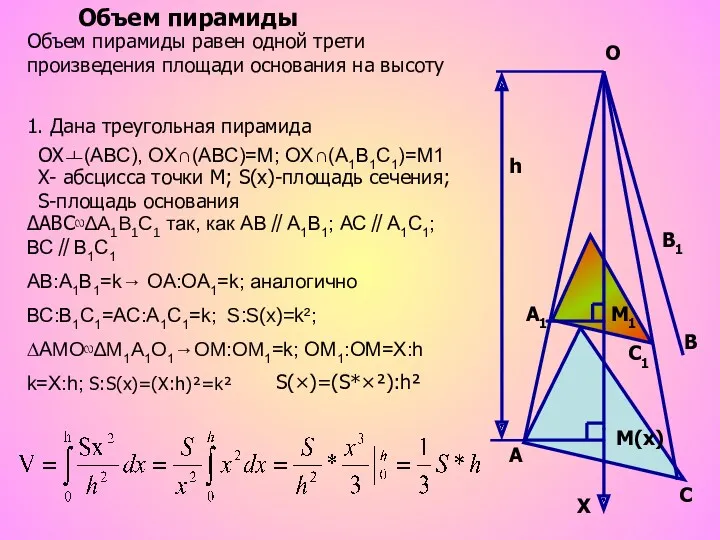
- 4. h A A1 B B1 C C1 M(х) M1 Объем пирамиды Объем пирамиды равен одной трети
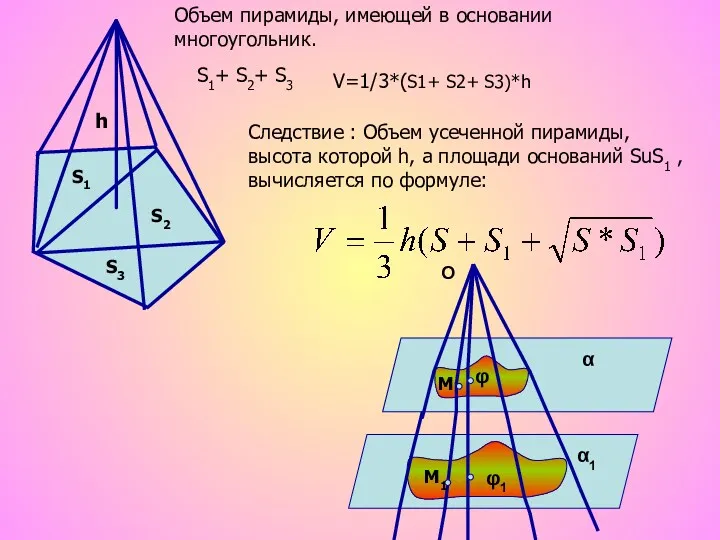
- 5. S1+ S2+ S3 S1 S2 S3 h V=1/3*(S1+ S2+ S3)*h Объем пирамиды, имеющей в основании многоугольник.
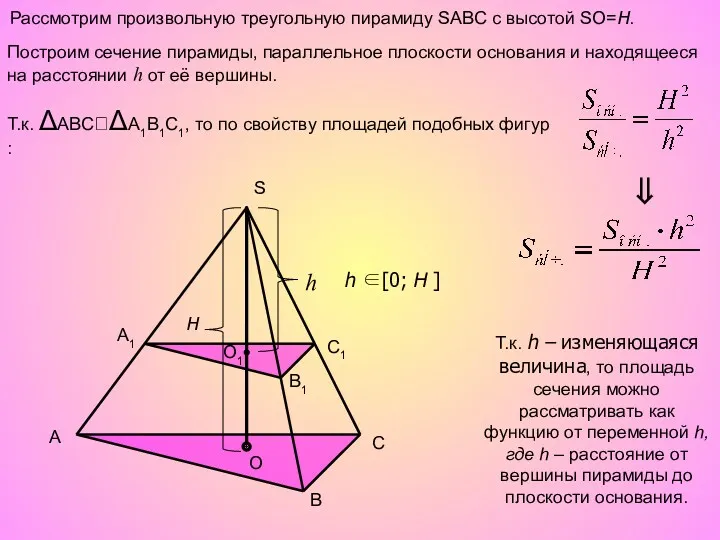
- 6. Рассмотрим произвольную треугольную пирамиду SABC с высотой SO=H. A B C S O H O1 h
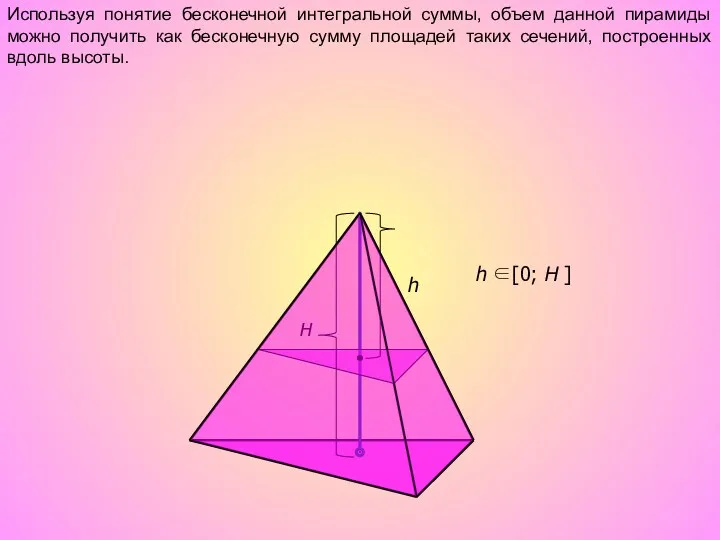
- 7. h H Используя понятие бесконечной интегральной суммы, объем данной пирамиды можно получить как бесконечную сумму площадей
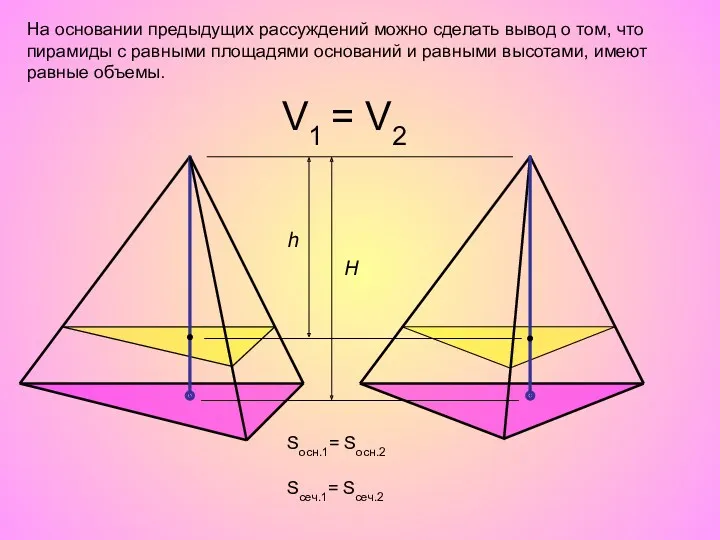
- 8. H Sосн.1= Sосн.2 V1 = V2 h Sсеч.1= Sсеч.2 На основании предыдущих рассуждений можно сделать вывод
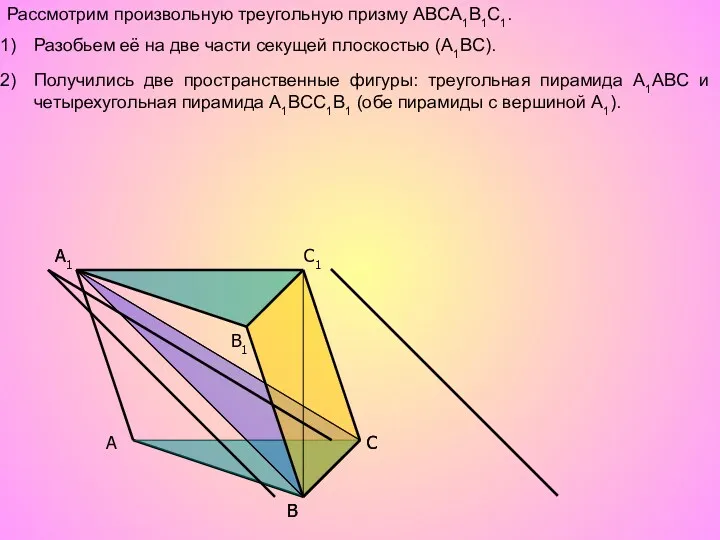
- 9. A B C B1 A1 C1 C A1 B Рассмотрим произвольную треугольную призму ABCA1B1C1. Разобьем её
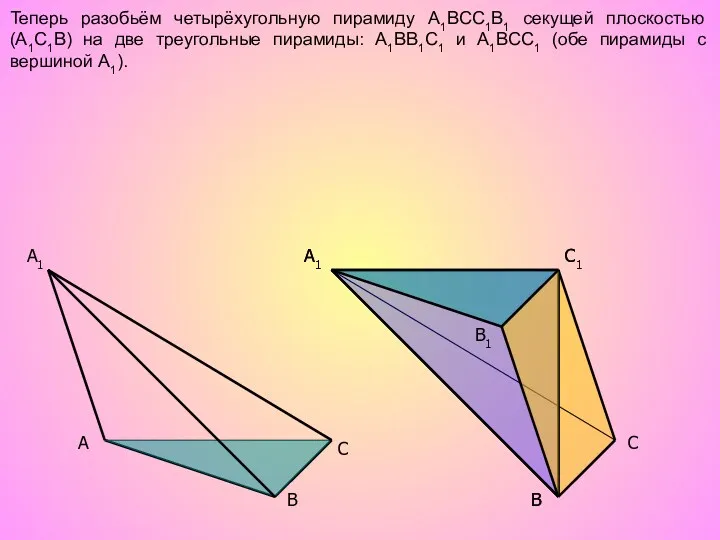
- 10. A C B1 A1 C1 C A1 B B Теперь разобьём четырёхугольную пирамиду A1BCC1B1 секущей плоскостью
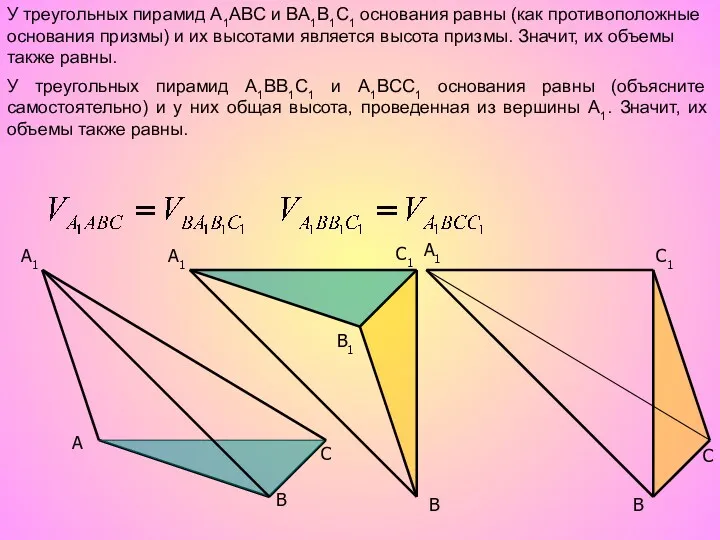
- 11. A C B1 A1 C1 C A1 B B A1 C1 B У треугольных пирамид A1ABC
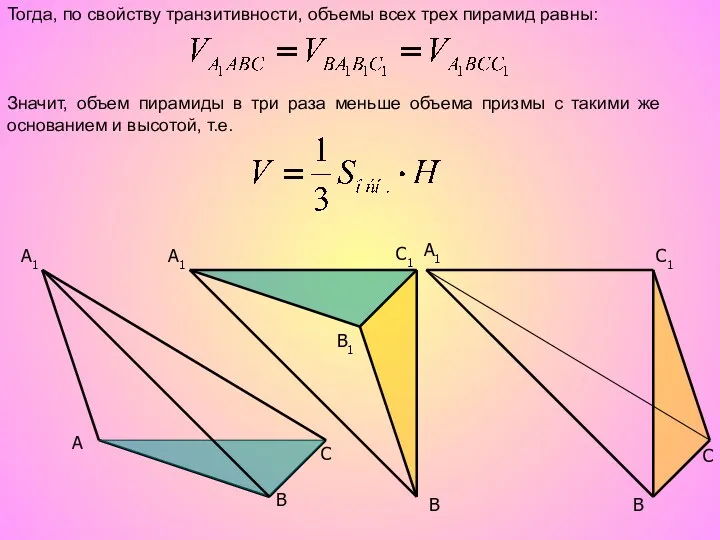
- 12. A C B1 A1 C1 C A1 B B A1 C1 B Тогда, по свойству транзитивности,
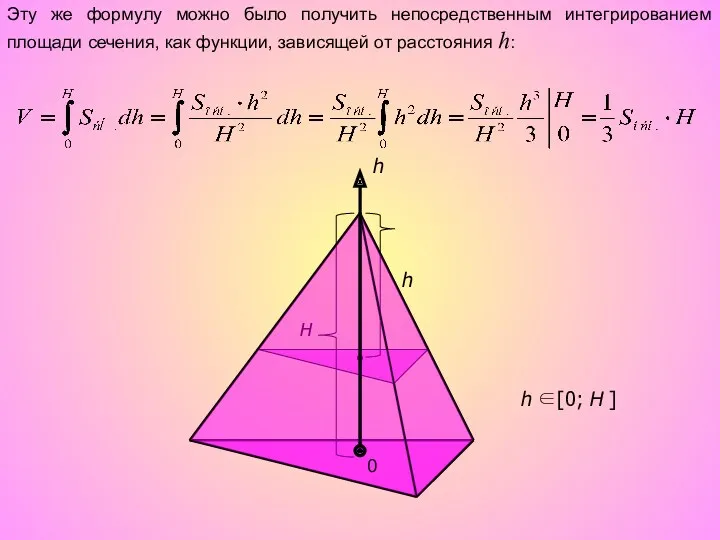
- 13. h H h Эту же формулу можно было получить непосредственным интегрированием площади сечения, как функции, зависящей
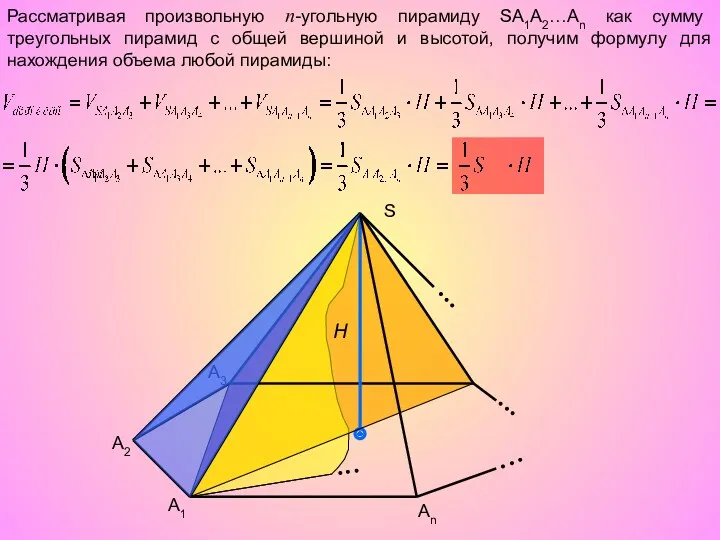
- 14. Рассматривая произвольную n-угольную пирамиду SA1A2…An как сумму треугольных пирамид с общей вершиной и высотой, получим формулу
- 15. Итак, для любой n-угольной пирамиды: ,где Sосн. – площадь основания пирамиды, H – высота пирамиды.
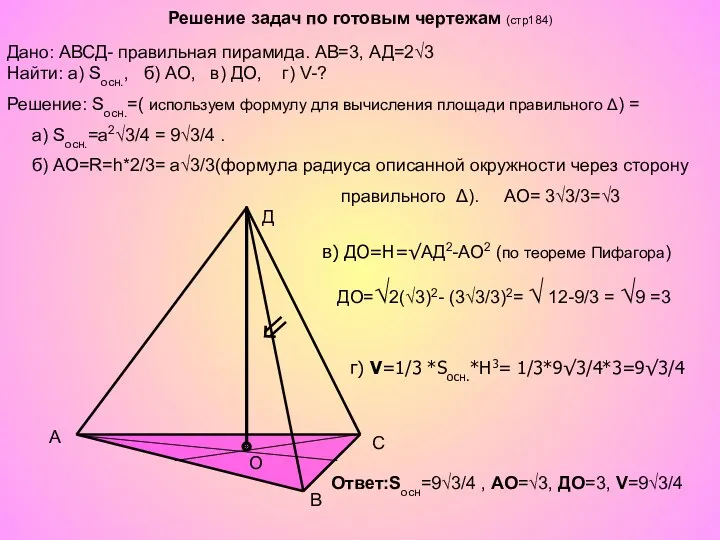
- 16. Решение задач по готовым чертежам (стр184) A B C Д O Дано: АВСД- правильная пирамида. АВ=3,
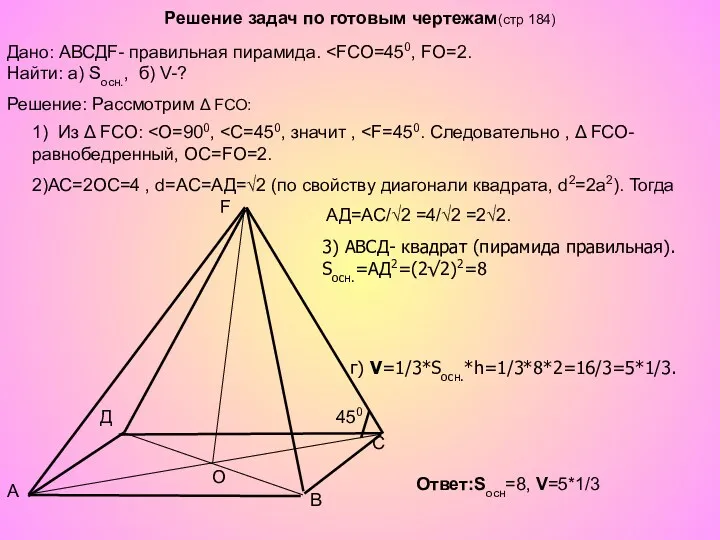
- 17. Решение задач по готовым чертежам(стр 184) A B C Д O Дано: АВСДF- правильная пирамида. Решение:
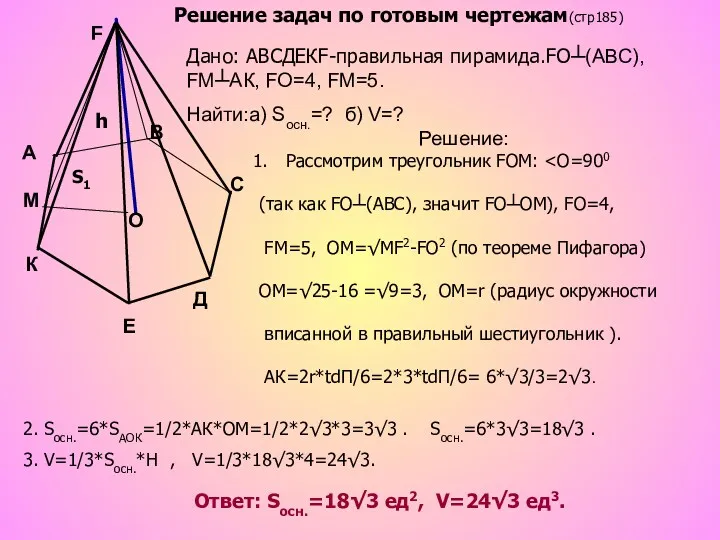
- 18. Дано: АВСДЕКF-правильная пирамида.FО┴(АВС), FМ┴АК, FO=4, FМ=5. Найти:а) Sосн.=? б) V=? Решение: S1 h Рассмотрим треугольник FОМ:
- 19. Свойство объемов №1 Равные тела имеют равные объемы Свойство объемов №2 Если тело составлено из нескольких
- 20. Домашнее задание П. 69, № 684а, 686а, 687.
- 21. Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев «Геометрия, 10-11», М., Просвещение, 2007 В.Я. Яровенко «Поурочные разработки по
- 23. Скачать презентацию






 Построение таблиц истинности для логических выражений
Построение таблиц истинности для логических выражений Уравнения и неравенства в ГИА. Математика 9 класс
Уравнения и неравенства в ГИА. Математика 9 класс Презентация урока математики Сложение, умк Перспектива, 1 класс.
Презентация урока математики Сложение, умк Перспектива, 1 класс. Математика. 1 класс. Урок 53. Таблица сложения - Презентация
Математика. 1 класс. Урок 53. Таблица сложения - Презентация доклад по теме: Критерии оценки по математике в начальной школе
доклад по теме: Критерии оценки по математике в начальной школе В царстве формул сокращенного умножения. Математический диктант
В царстве формул сокращенного умножения. Математический диктант Презентация для детей Состав числа
Презентация для детей Состав числа Туынды. Алғашқы функция. Интеграл
Туынды. Алғашқы функция. Интеграл Анализ упражнений на нумерацию чисел концентра сотня в учебниках по математике Л.Г. Петерсон
Анализ упражнений на нумерацию чисел концентра сотня в учебниках по математике Л.Г. Петерсон Решение задач на готовых чертежах. Площади фигур. (8 класс)
Решение задач на готовых чертежах. Площади фигур. (8 класс) Математика. ЕГЭ. Стереометрия 2
Математика. ЕГЭ. Стереометрия 2 Периметр
Периметр Понятие о десятичной дроби
Понятие о десятичной дроби Координаты на прямой
Координаты на прямой Выпуклость и точки перегиба графика функции. Асимптоты. Лекция № 3
Выпуклость и точки перегиба графика функции. Асимптоты. Лекция № 3 Численное интегрирование функций
Численное интегрирование функций Функции и их свойства. Алгебра 9 класс
Функции и их свойства. Алгебра 9 класс 1-2 класс. Интерактивная игра-тренажёр Зимняя сказка (сложение в пределах 20)
1-2 класс. Интерактивная игра-тренажёр Зимняя сказка (сложение в пределах 20) Множества на кругах Эйлера-Венна
Множества на кругах Эйлера-Венна Пирамида
Пирамида Площадь круга
Площадь круга Проверочная работа по теме Углы и многоугольники
Проверочная работа по теме Углы и многоугольники Прямая и обратная пропорциональные зависимости. (6 класс)
Прямая и обратная пропорциональные зависимости. (6 класс) Больше. Меньше. Столько же
Больше. Меньше. Столько же Нумерация_1000
Нумерация_1000 Статистические данные
Статистические данные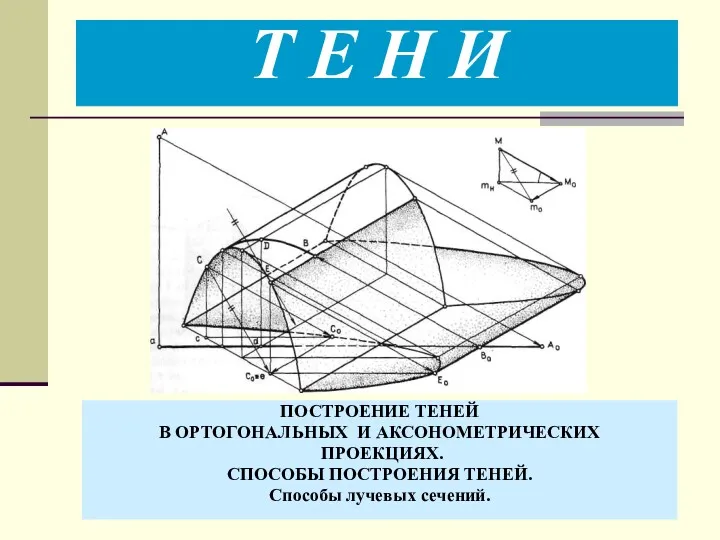 Тени. Построение теней в ортогональных и аксонометрических проекциях. Способы построения теней. Способы лучевых сечений
Тени. Построение теней в ортогональных и аксонометрических проекциях. Способы построения теней. Способы лучевых сечений Урок математики Свойства сложения
Урок математики Свойства сложения