Содержание
- 2. Литература В. М. Вержбицкий, Основы численных методов, Высшая школа, 2005 г. А.А. Амосов, Ю.А. Дубинский, Н.В.
- 3. Решение нелинейных алгебраических уравнений Пусть функция f(x) определена и непрерывна при всех х на отрезке [а,b]
- 4. Решение нелинейных алгебраических уравнений. Алгоритм метода половинного деления В. М. Вержбицкий, Основы численных методов, Высшая школа,
- 5. Блок-схема метода половинного деления
- 6. Решение нелинейных алгебраических уравнений. Алгоритм метода секущих В. М. Вержбицкий, Основы численных методов, Высшая школа, 2005
- 7. Решение нелинейных алгебраических уравнений. Алгоритм метода Стеффенсена В. М. Вержбицкий, Основы численных методов, Высшая школа, 2005
- 8. Решение нелинейных алгебраических уравнений. Алгоритм метода простой итерации Чтобы применить метод простой итерации необходимо преобразовать исходное
- 9. Трёхдиагональная СЛАУ Трёхдиагональными называются матрицы, каждая строка которых содержит 3 соседних неизвестных: bixi-1+cixi+dixi+1=ri, b1=0, dn=0, i=1..n
- 10. Системы линейных алгебраических уравнений (СЛАУ) СЛАУ в матричном виде записывается как А*x=b, где В Excel удобно
- 11. Решение трёхдиагональной СЛАУ методом прогонки Прямой ход метода прогонки: Определение коэффициентов δi, λi, i=2..n δ1=-d1/c1; λ1=r1/c1
- 12. Решение СЛАУ методом Гаусса Прямой ход метода Гаусса (приведение к треугольному виду) Обратный ход метода Гаусса
- 13. Алгоритм решения СЛАУ методом Гаусса В. М. Вержбицкий, Основы численных методов, Высшая школа, 2005 г
- 14. LU-разложение Любая матрица А(n x n) может быть преобразована представлена как произведение нижней (L) и верхней
- 15. LU-разложение (продолжение) Из оставшейся части 2-й строки u2j=a2j-l21u1j (j=2,...,n) Из оставшейся части 2-го столбца li2=(ai2-li1u12)/u22 (i=3,…,n)
- 16. Решение СЛАУ при помощи LU-разложения Система Ax=b преобразуется к LUx=b Или, вводя вектор вспомогательных переменных y:
- 17. Решение СЛАУ методом простых итераций Сначала надо привести функцию, удобному для метода итераций: x=ϕ(x). Итерационная процедура
- 18. Решение СЛАУ методом Зейделя Вариант метода простых итераций, где часть переменных хk заменена на xk+1 В.
- 19. Одномерная оптимизация. Метод деления отрезка пополам
- 20. Одномерная оптимизация. Метод деления отрезка пополам А. В. Пантелеев, Т. А. Летова. Методы оптимизации в примерах
- 21. Одномерная оптимизация. Метод золотого сечения А. В. Пантелеев, Т. А. Летова Методы оптимизации в примерах и
- 22. Одномерная оптимизация. Метод Фибоначчи
- 23. Одномерная оптимизация. Метод Фибоначчи (продолжение) А. В. Пантелеев, Т. А. Летова Методы оптимизации в примерах и
- 24. Одномерная оптимизация. Метод квадратичной интерполяции А. В. Пантелеев, Т. А. Летова Методы оптимизации в примерах и
- 25. Одномерная оптимизация. Метод квадратичной интерполяции (продолжение)
- 26. Интерполяционный полином Лагранжа В. М. Вержбицкий, Основы численных методов, Высшая школа, 2005 г. Для заданной таблично
- 27. Линейная задача наименьших квадратов (МНК) Функция y=f(x) задана таблицей приближенных значений yi≈f(xi), i=0..n Для аппроксимации используется
- 28. Метод МНК (продолжение) Из различных критериев выбора параметров ai наиболее часто используется критерий наименьших квадратов. Согласно
- 29. Метод МНК (продолжение) Опуская промежуточные выкладки, для получения параметров ai требуется решить СЛАУ: Или для случая
- 30. Метод МНК (продолжение) Для m=1, P1=a0+a1x Нормальная система имеет вид: Для m=2, P1=a0+a1x+a2x2 Нормальная система имеет
- 31. Интегрирование. Формулы прямоугольников, трапеций и Симпсона Квадратурные формулы левых и правых прямоугольников Формула трапеций Формула Симпсона
- 32. Квадратурные формулы Квадратурные формулы: Хi – узлы; Аi – веса; В ранее рассмотренных формулах узлы равноотстоящие
- 33. Квадратурные формулы (продолжение) Целесообразно отказаться от равноотстоящих узлов и преобразовать: Целесообразно отказаться от равноотстоящих узлов и
- 34. Квадратурная формула Чебышева При Аi ≡ A = 2/n и таких ti, что формула точна для
- 35. Квадратурная формула Гаусса При неравенстве Аi друг другу квадратурная формула имеет более общий вид. Узлами её
- 36. Узлы и веса для квадратур Чебышева и Гаусса
- 37. Решение задачи Коши для обыкновенных дифференциальных уравнений ОДУ 1-го порядка: y’=f(x,y), x∈[x0,b] Начальное условие – y(x0)=y0
- 39. Скачать презентацию
 Урок математики для учащихся 2 класса по теме Сложение и вычитание двузначных чисел
Урок математики для учащихся 2 класса по теме Сложение и вычитание двузначных чисел Степень с целым показателем. 8 класс
Степень с целым показателем. 8 класс Сложение и вычитание. 3 класс
Сложение и вычитание. 3 класс Модуль числа
Модуль числа Связь между компонентами и результатом умножения
Связь между компонентами и результатом умножения Единицы массы. Центнер. Тонна
Единицы массы. Центнер. Тонна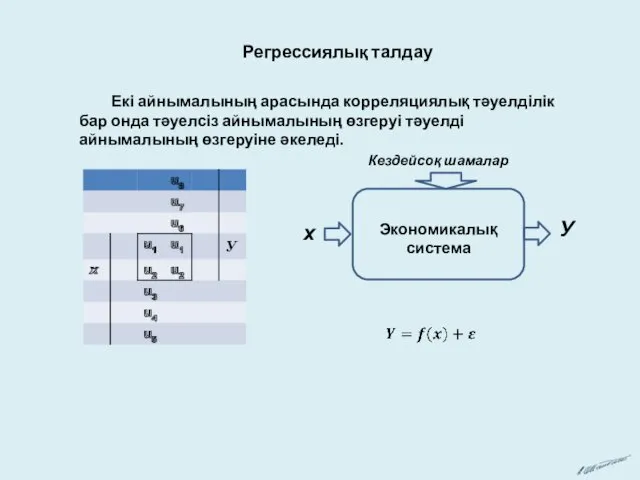 Регрессиялық талдау
Регрессиялық талдау Закрепление изученного. Решение задач
Закрепление изученного. Решение задач Теорема о пропорциональных отрезках. Теорема Фалеса 2
Теорема о пропорциональных отрезках. Теорема Фалеса 2 Геометрические фигуры в стихах и картинках
Геометрические фигуры в стихах и картинках Перпендикулярні прямі
Перпендикулярні прямі Тренажер Таблица умножения и деления.
Тренажер Таблица умножения и деления. Возможные косвенные показатели для улучшения мультиколлинеарности
Возможные косвенные показатели для улучшения мультиколлинеарности Метод Гаусса
Метод Гаусса Производная сложной функции
Производная сложной функции Решение стереометрических задач при подготовке к ЕГЭ
Решение стереометрических задач при подготовке к ЕГЭ Турнир юных математиков
Турнир юных математиков Линейные уравнения
Линейные уравнения презентация по наглядной геометрии
презентация по наглядной геометрии Презинтация Цвет и Форма Диск
Презинтация Цвет и Форма Диск Основная теория по алгебре для ОГЭ
Основная теория по алгебре для ОГЭ Многочлены. Умножение многочлена на многочлен. Формулы квадрата суммы и квадрата разности
Многочлены. Умножение многочлена на многочлен. Формулы квадрата суммы и квадрата разности Презентация по теме Вычитание вида 35-15
Презентация по теме Вычитание вида 35-15 Угол между векторами. Скалярное произведенне векторов
Угол между векторами. Скалярное произведенне векторов Переместительное свойство умножения
Переместительное свойство умножения Теория пределов
Теория пределов Как появились натуральные числа
Как появились натуральные числа Нестандартные способы решения квадратных уравнений
Нестандартные способы решения квадратных уравнений