Окружность и круг в задачах повышенного уровня сложности по планиметрии в КИМ на ЕГЭ по математике презентация
Содержание
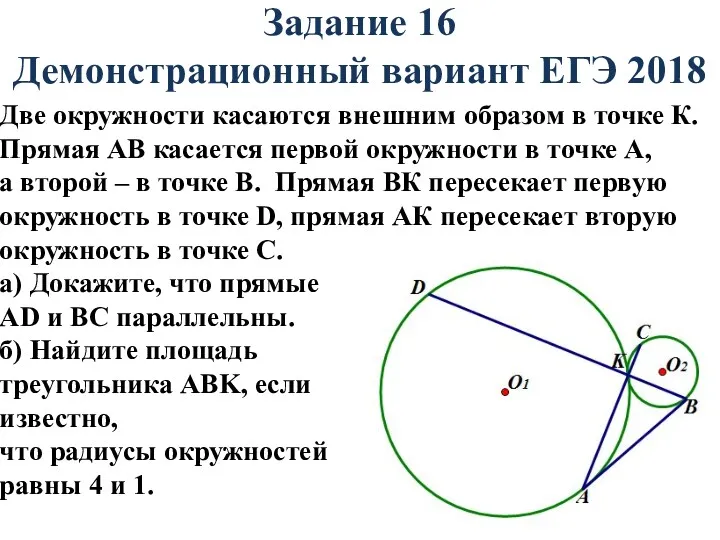
- 2. Задание 16 Демонстрационный вариант ЕГЭ 2018 Две окружности касаются внешним образом в точке К. Прямая АВ
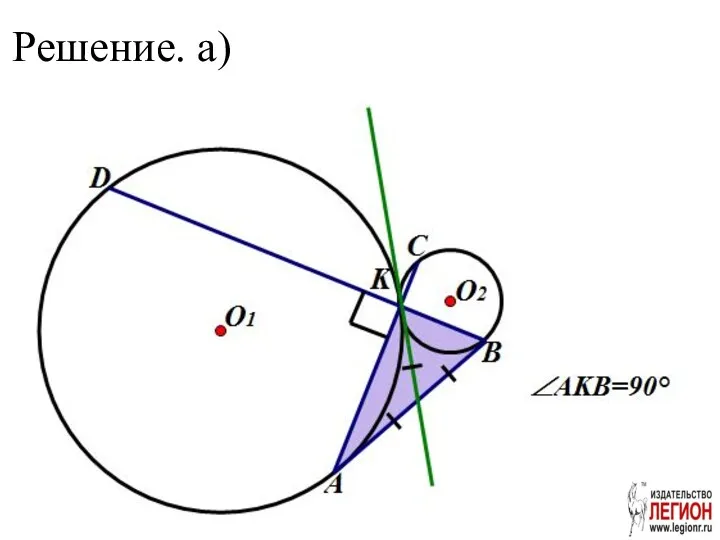
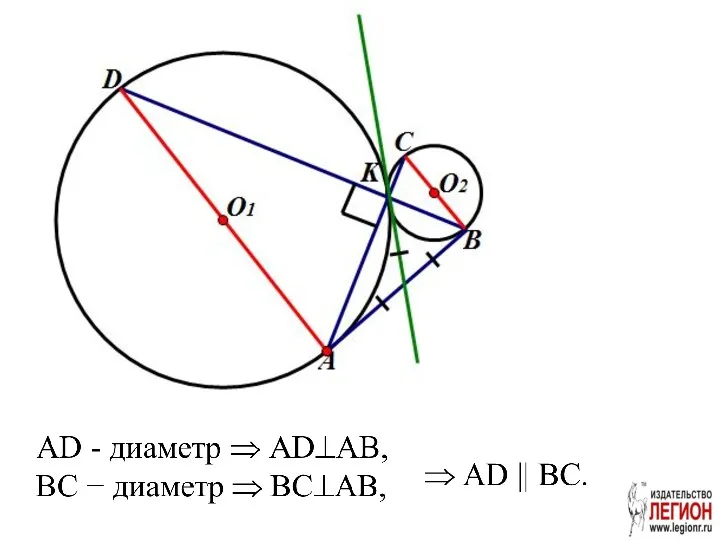
- 3. Решение. а)
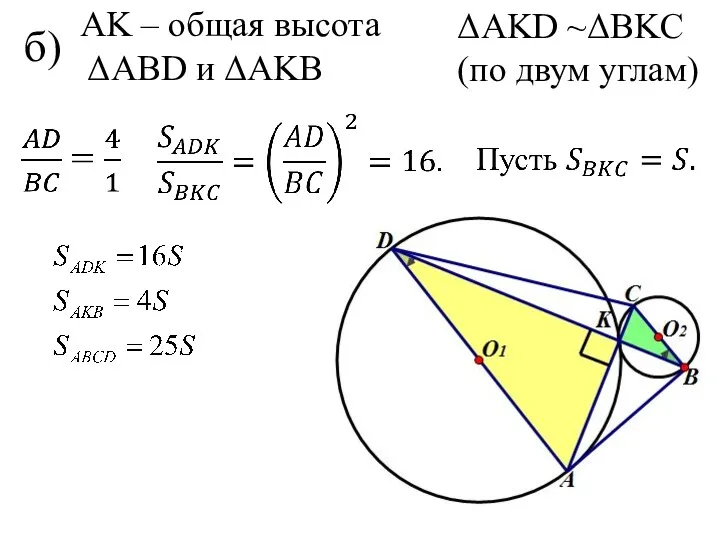
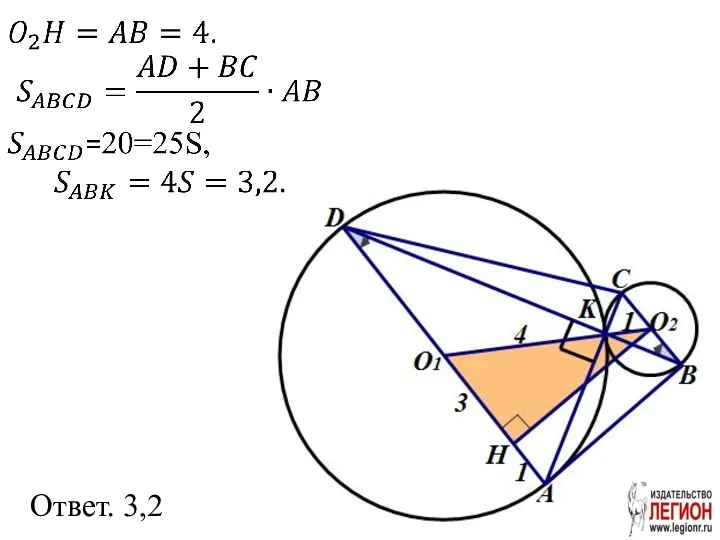
- 5. б) ΔAKD ~ΔBKC (по двум углам) AK – общая высота ΔAВD и ΔAKВ
- 6. Ответ. 3,2
- 7. Задача 2
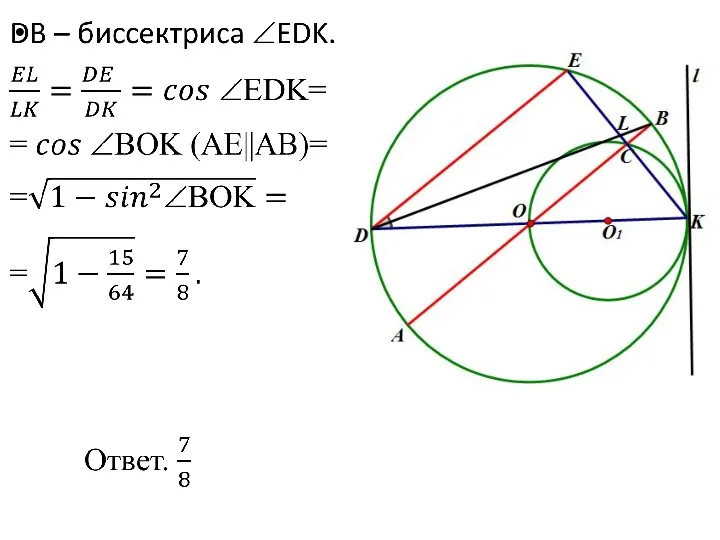
- 8. а) ∠DEK=∠OCK=90° ⇒ ⇒ DE||AB. l- общая касательная, OK ⊥ l, O1K ⊥ l ⇒ D,O,
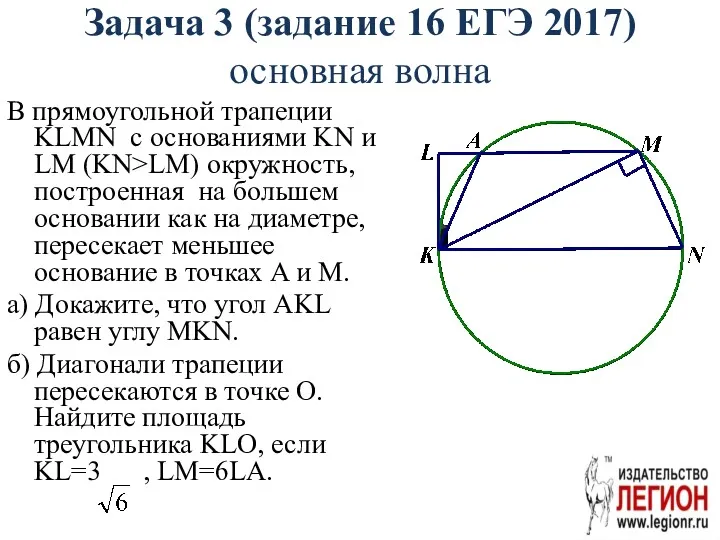
- 10. Задача 3 (задание 16 ЕГЭ 2017) основная волна В прямоугольной трапеции KLMN с основаниями KN и
- 11. Рассмотрим два случая: 1. ∠ MNK= 90°. MC=NC, что невозможно (катет не равен гипотенузе). 2. ∠
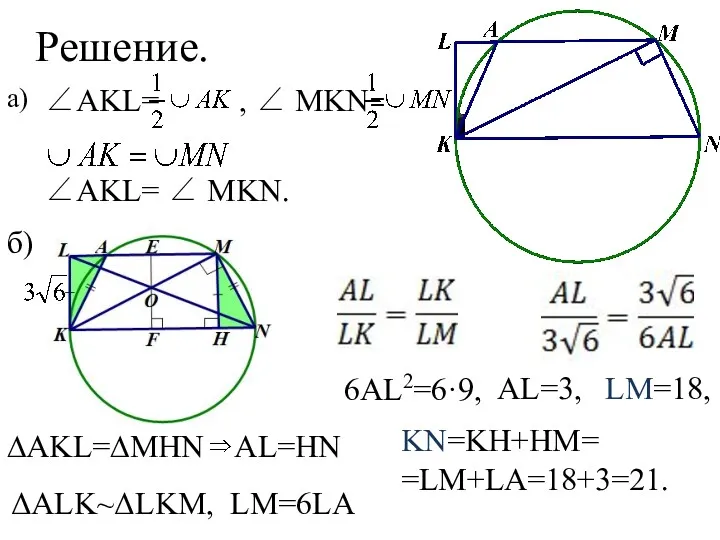
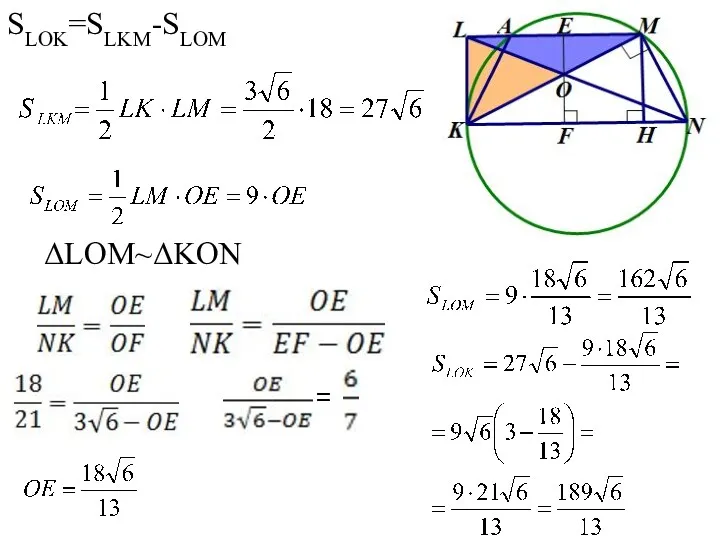
- 12. Решение. ∠AKL= , ∠ MKN= ∠AKL= ∠ MKN. а) б) ∆AKL=∆MHN AL=HN ΔALK~ΔLKM, LM=6LA 6AL2=6·9, AL=3,
- 13. SLOK=SLKM-SLOM ΔLOM~ΔKON =
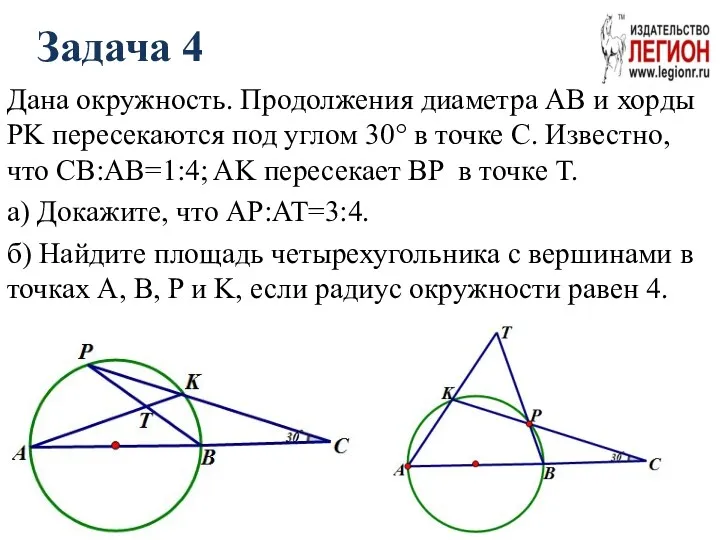
- 14. Задача 4 Дана окружность. Продолжения диаметра AB и хорды PK пересекаются под углом 30° в точке
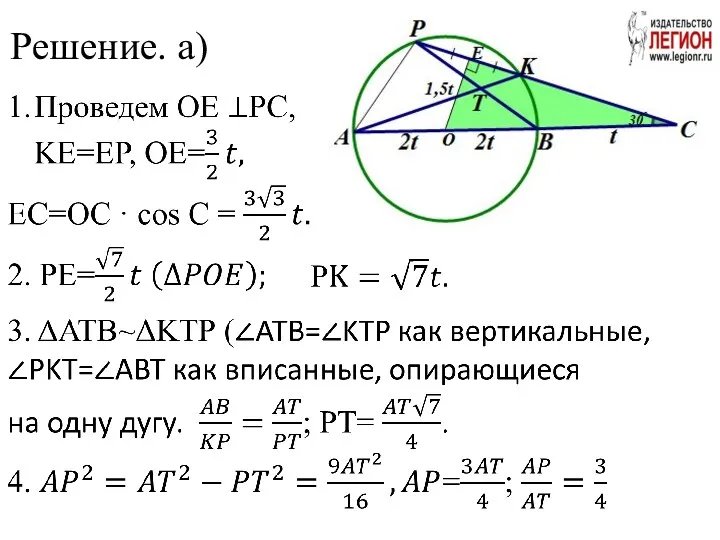
- 15. Решение. а)
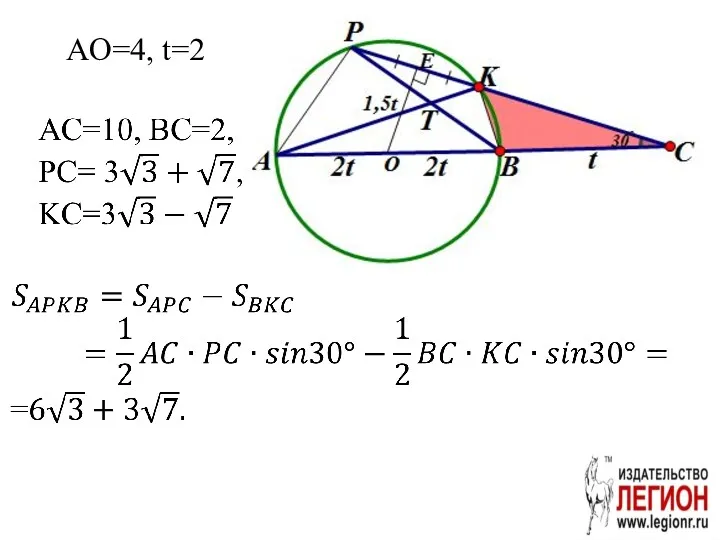
- 16. AO=4, t=2
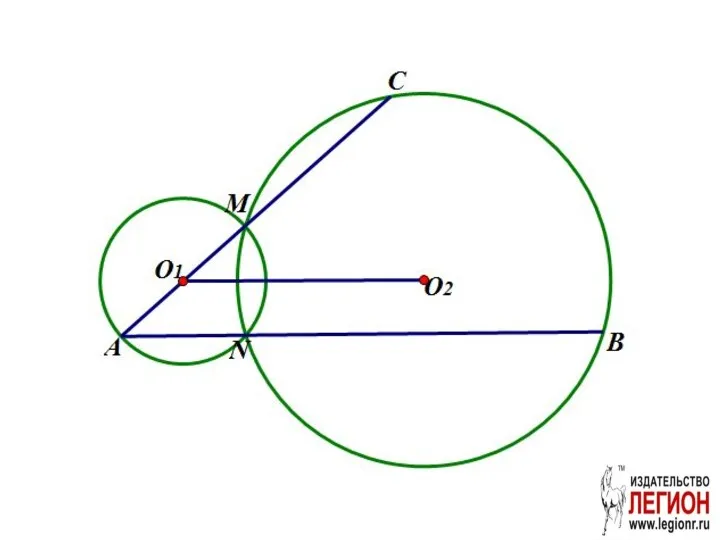
- 17. Задача 5 (№16 вариант 15 «Легион» ЕГЭ 2018 ) Две окружности с центрами O1 и O2
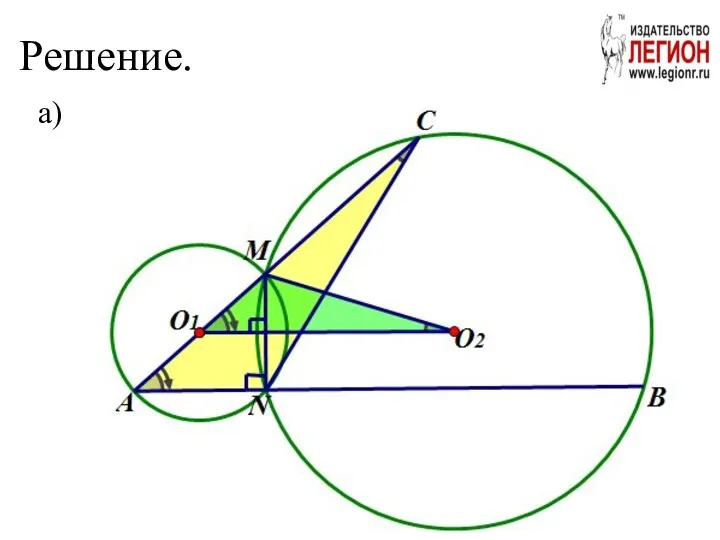
- 19. Решение. а)
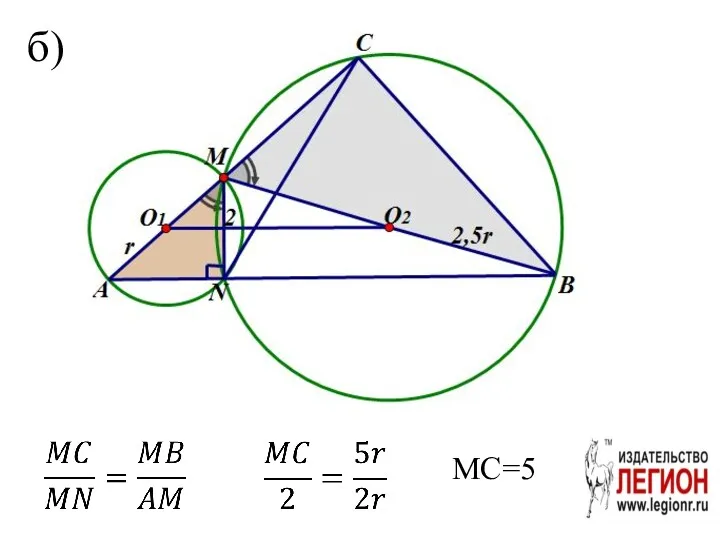
- 20. б) MC=5
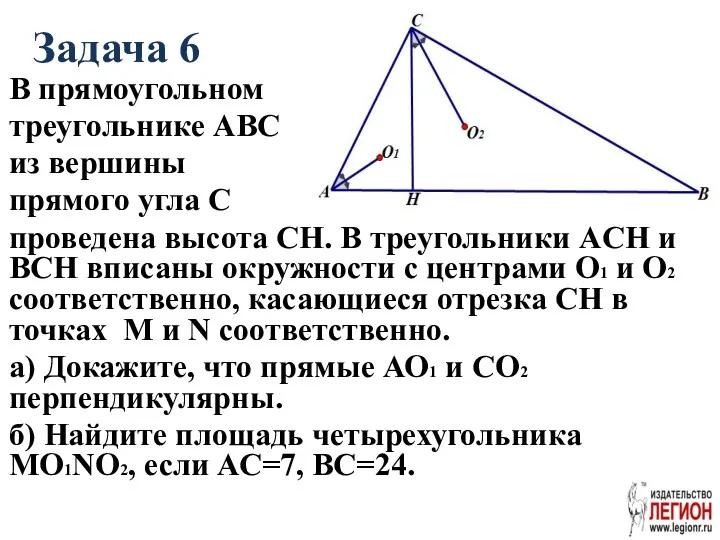
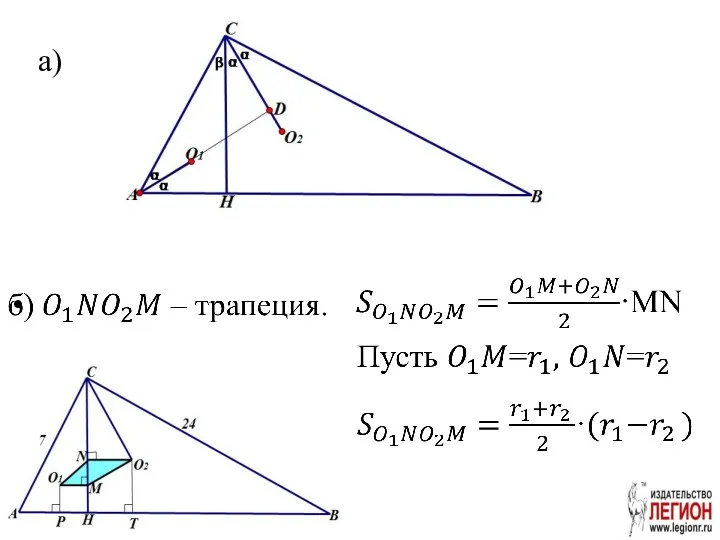
- 21. Задача 6 В прямоугольном треугольнике АВС из вершины прямого угла С проведена высота CH. В треугольники
- 22. а)
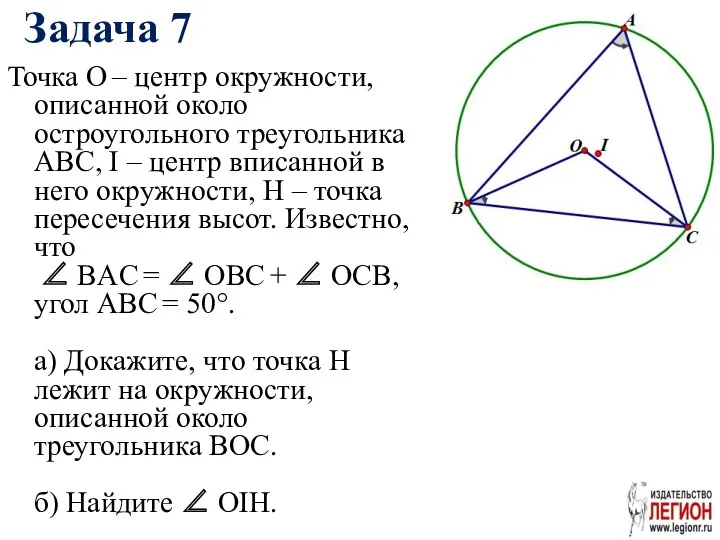
- 24. Задача 7 Точка О – центр окружности, описанной около остроугольного треугольника ABC, I – центр вписанной
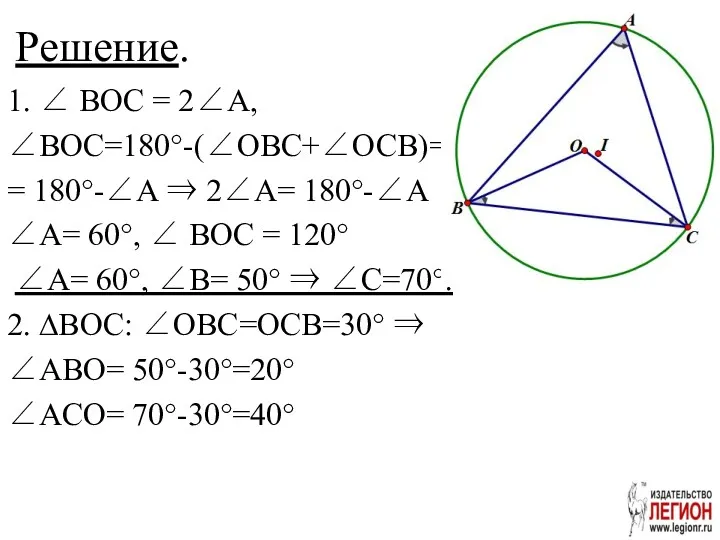
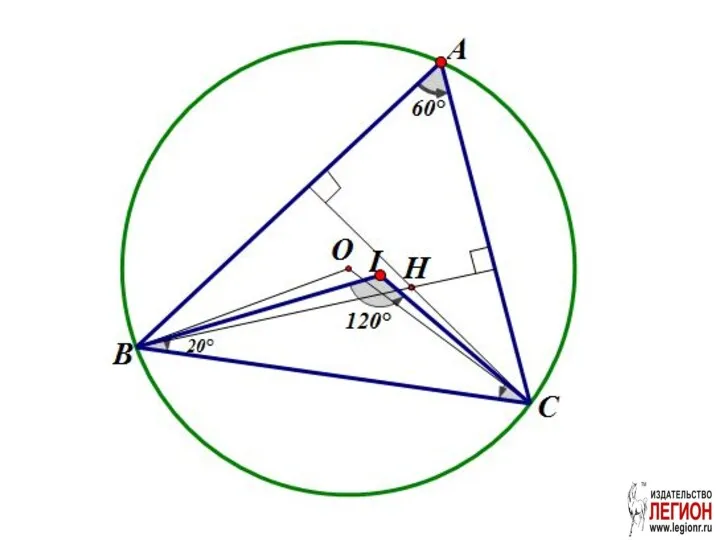
- 25. Решение. 1. ∠ BOC = 2∠A, ∠BOC=180°-(∠OBC+∠OCB)= = 180°-∠A ⇒ 2∠A= 180°-∠A ∠A= 60°, ∠ BOC
- 27. ∠ OIH+ ∠ OBH=180°, ∠ OBH=10° ⇒ ∠ OIH=170°
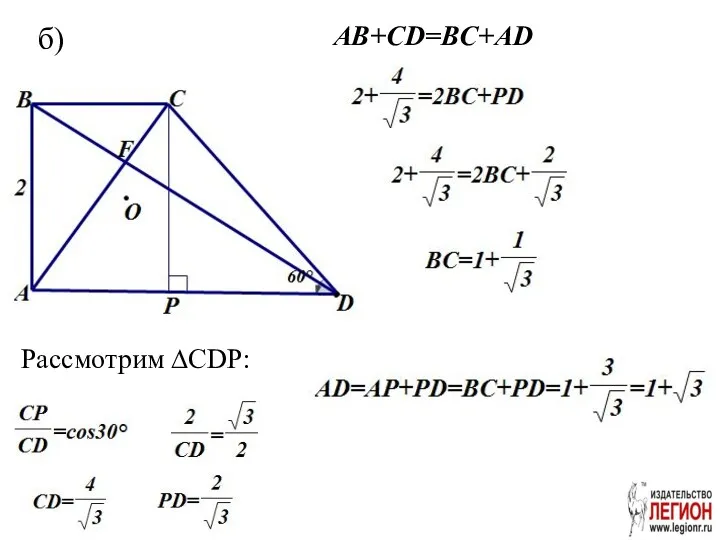
- 28. Задача 8 а) Докажите, что . б) Найдите расстояние от точки О до точки пересечения диагоналей
- 29. а)
- 30. Рассмотрим ∆CDP: AB+CD=BC+AD б)
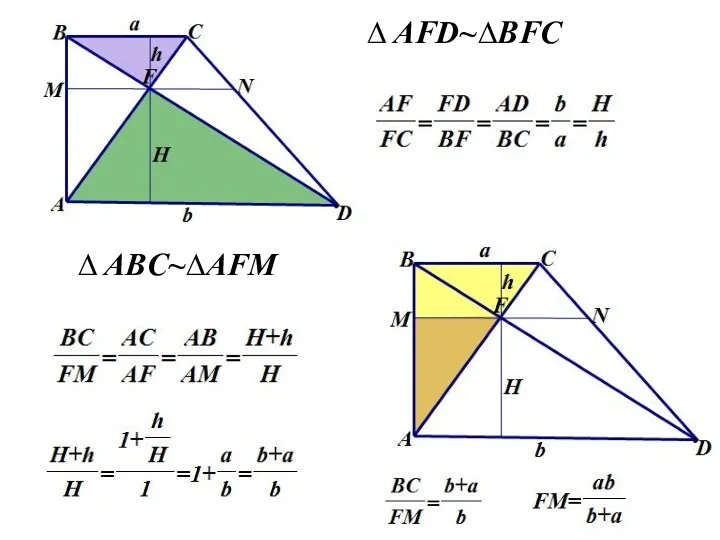
- 31. ∆ AFD~∆BFC ∆ ABC~∆AFM
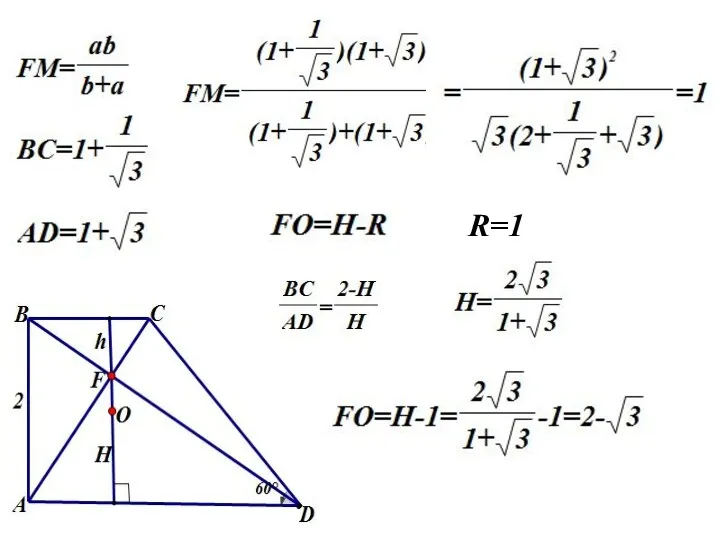
- 32. R=1
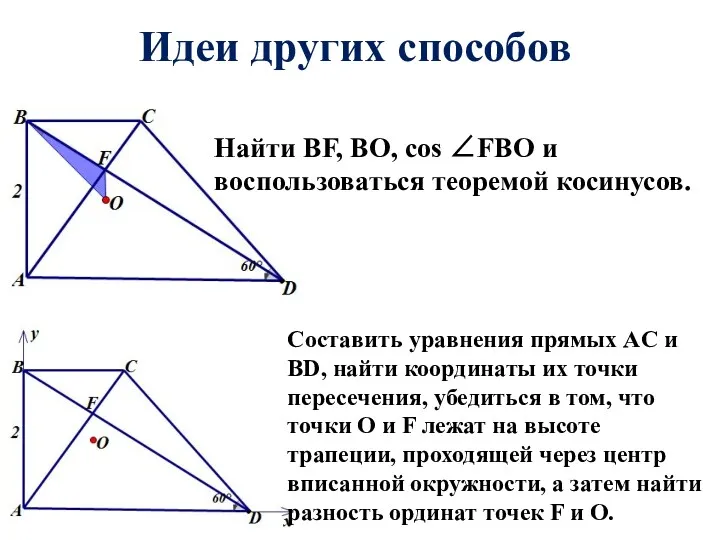
- 33. Идеи других способов Найти BF, BO, cos ∠FBO и воспользоваться теоремой косинусов. Составить уравнения прямых AC
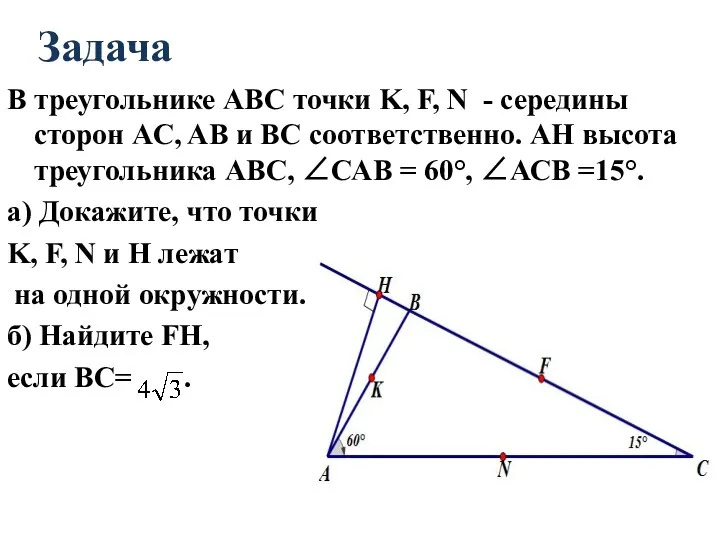
- 34. Задача В треугольнике АВС точки K, F, N - середины сторон AC, AB и BC соответственно.
- 35. Решение. ∠KHB=∠KBH=75°, HFNK – равнобедренная трапеция,⇒ ∠HKN=∠KNF=105°, ∠KHF=∠NFH=75°, тогда ∠KHF+∠KNF= ∠HKN+∠NFH=180°, это означает, что точки K,
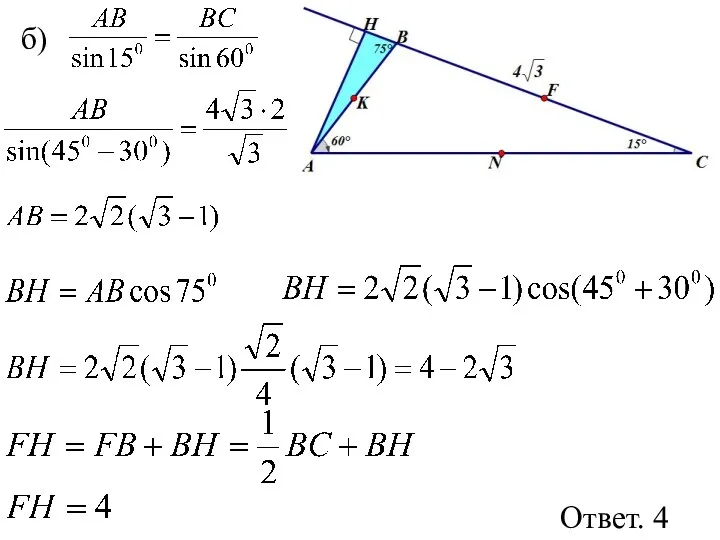
- 36. б) Ответ. 4
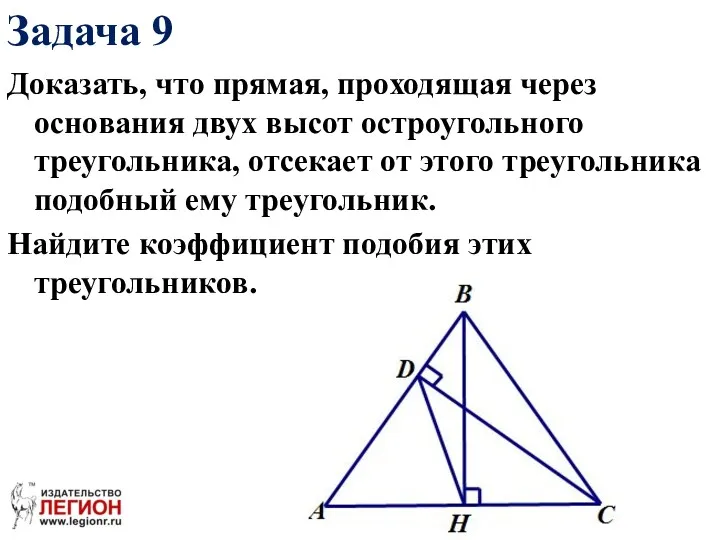
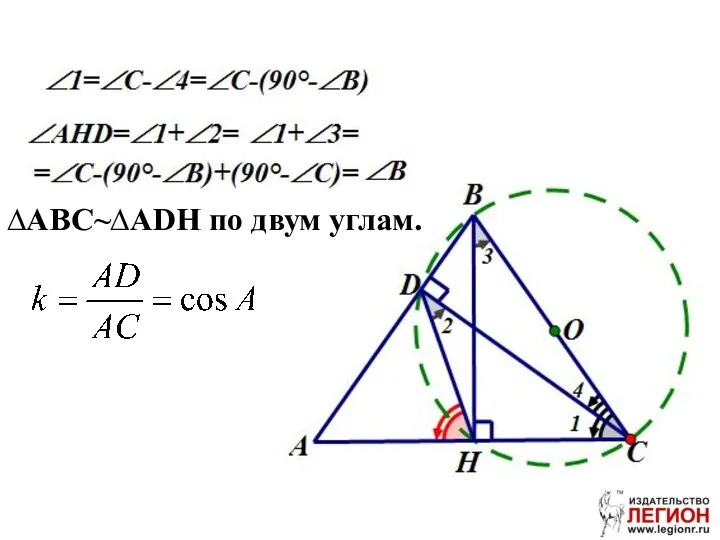
- 37. Доказать, что прямая, проходящая через основания двух высот остроугольного треугольника, отсекает от этого треугольника подобный ему
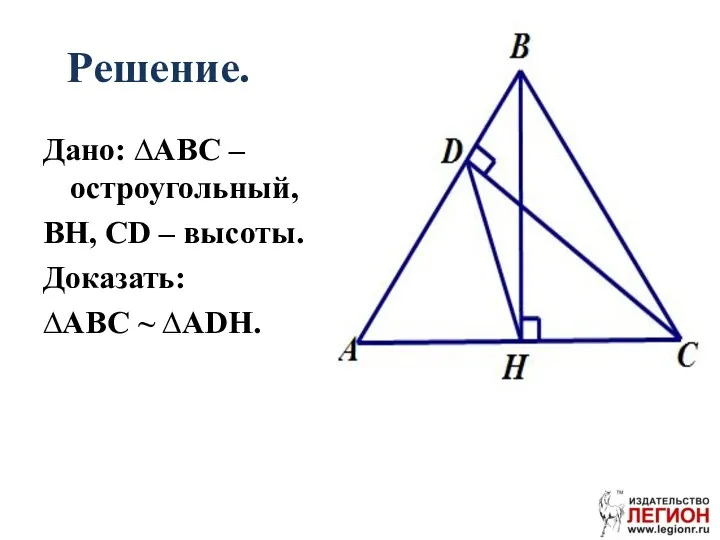
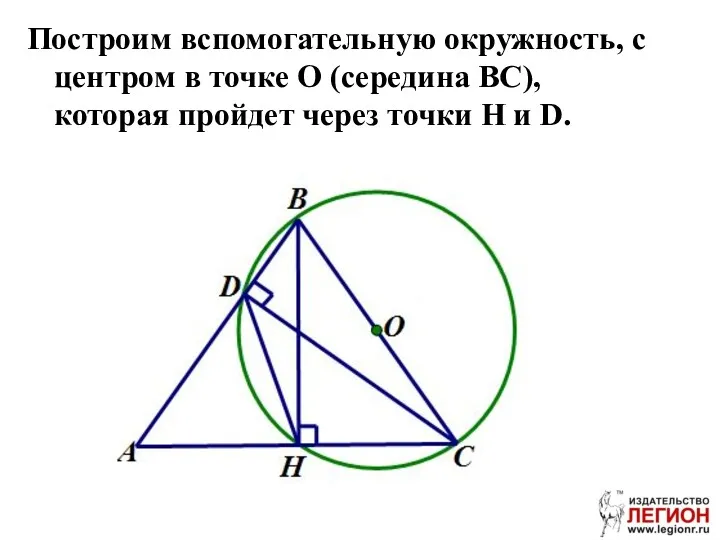
- 38. Решение. Дано: ∆ABC – остроугольный, BH, CD – высоты. Доказать: ∆ABC ~ ∆ADH.
- 39. Построим вспомогательную окружность, с центром в точке О (середина ВС), которая пройдет через точки H и
- 40. ∆ABC~∆ADH по двум углам.
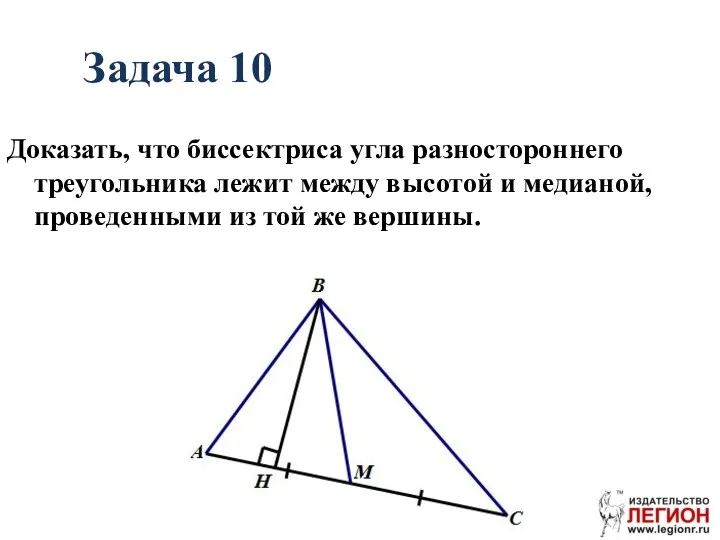
- 41. Задача 10 Доказать, что биссектриса угла разностороннего треугольника лежит между высотой и медианой, проведенными из той
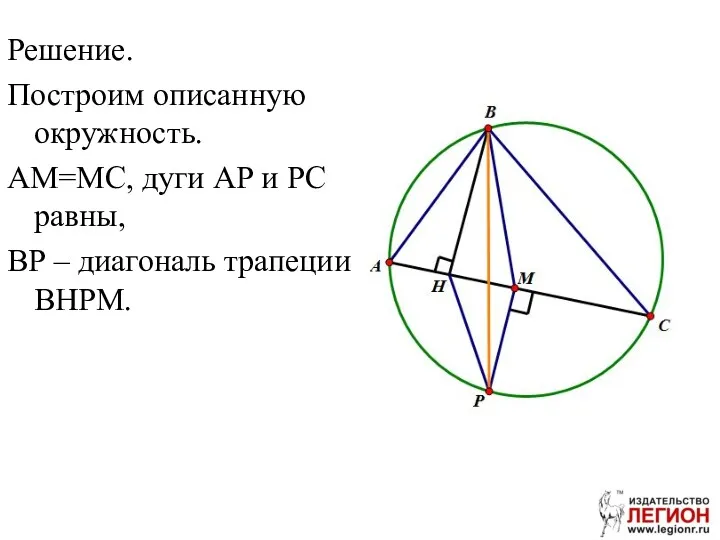
- 42. Решение. Построим описанную окружность. АМ=МС, дуги АР и РС равны, ВР – диагональ трапеции ВНРМ.
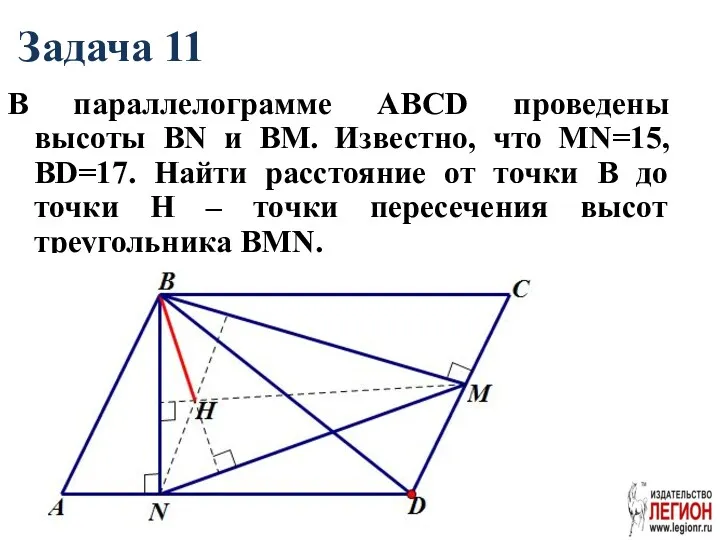
- 43. Задача 11 В параллелограмме АВСD проведены высоты ВN и ВМ. Известно, что МN=15, ВD=17. Найти расстояние
- 44. Решение. Ответ. 8
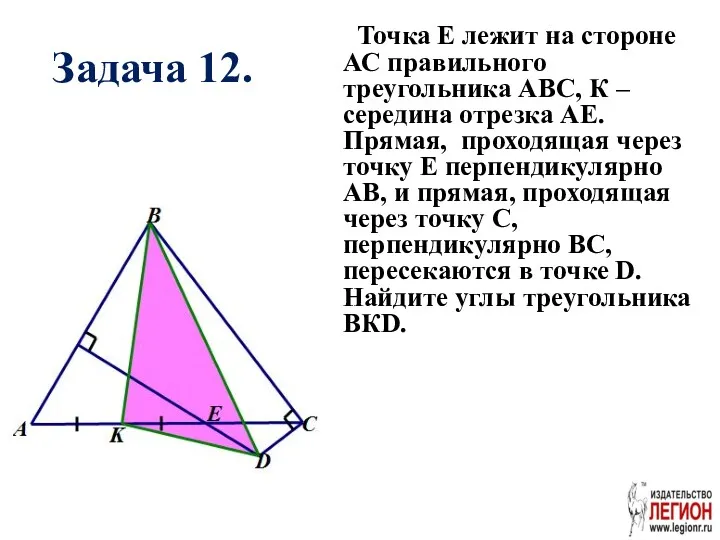
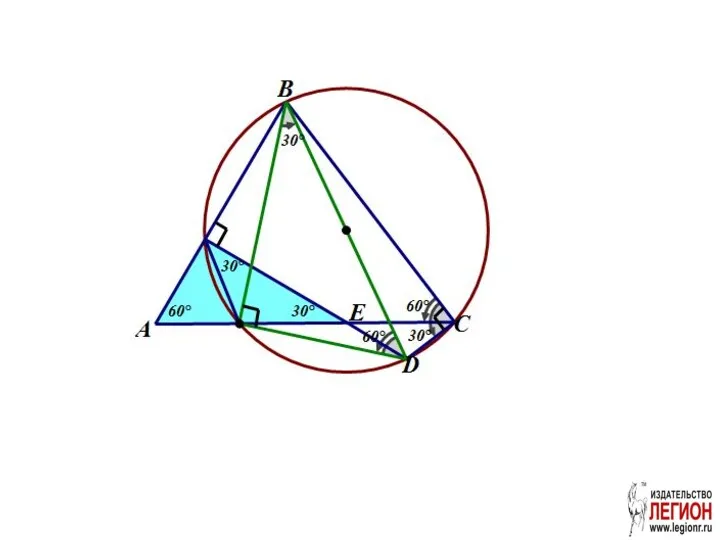
- 45. Задача 12. Точка Е лежит на стороне АС правильного треугольника АВС, К – середина отрезка АЕ.
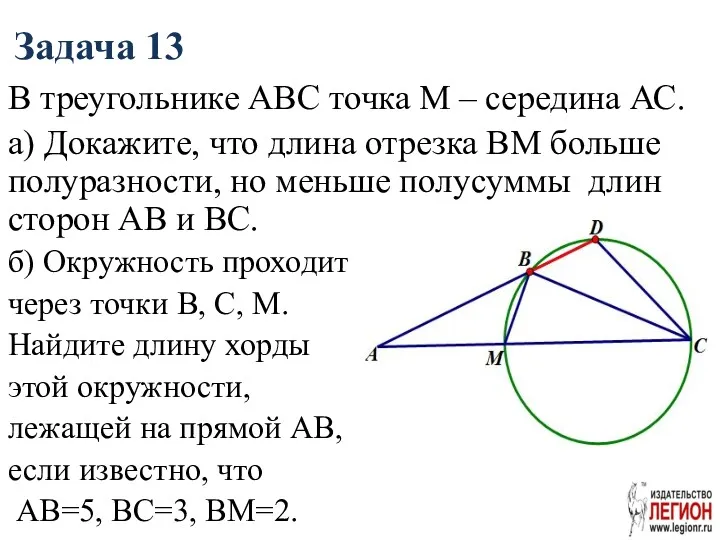
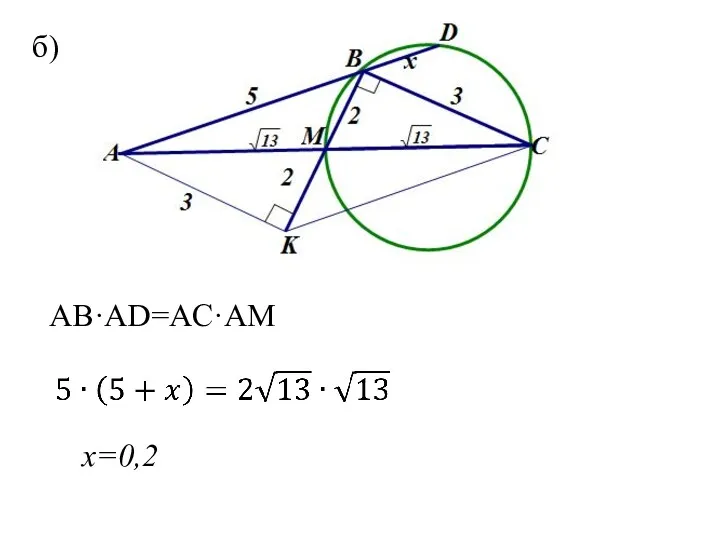
- 48. Задача 13 В треугольнике АВС точка М – середина АС. а) Докажите, что длина отрезка ВМ
- 49. б) AB·AD=AC·AM x=0,2
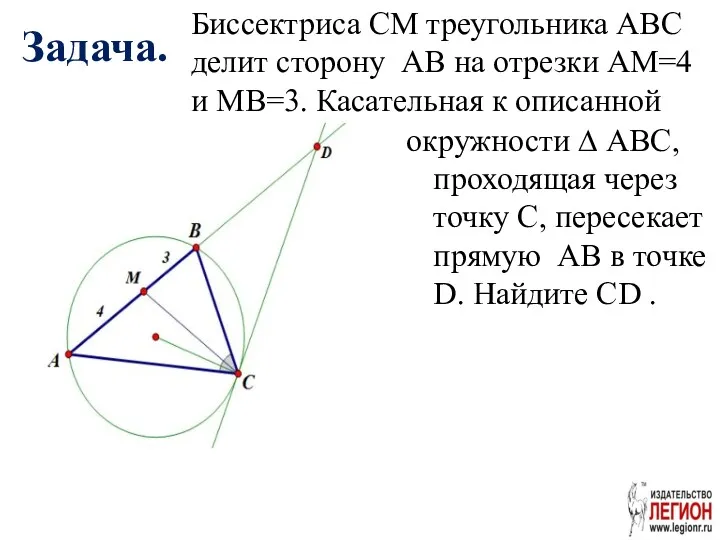
- 50. Задача. окружности ∆ ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD
- 51. Решение. Ответ. 12 По свойству касательной
- 56. Скачать презентацию















 Скалярное произведение векторов
Скалярное произведение векторов Презентация Умножение двузначного числа на однозначное 3 класс Планета знаний
Презентация Умножение двузначного числа на однозначное 3 класс Планета знаний Все действия с дробями. Урок математики в 5 классе
Все действия с дробями. Урок математики в 5 классе Презентация Молчанка (устный счет, 4 класс)
Презентация Молчанка (устный счет, 4 класс) Линейная функция и её график
Линейная функция и её график Презентация Математика вокруг нас
Презентация Математика вокруг нас Вычесть число 3.
Вычесть число 3. Понятие определенного интеграла
Понятие определенного интеграла Сызықтық емес (бейсызықтық) жұп регрессия
Сызықтық емес (бейсызықтық) жұп регрессия Дроби. Нахождение части числа. Нахождение целого по его части.
Дроби. Нахождение части числа. Нахождение целого по его части. Решение логических задач
Решение логических задач Знаходження невідомого зменшуваного
Знаходження невідомого зменшуваного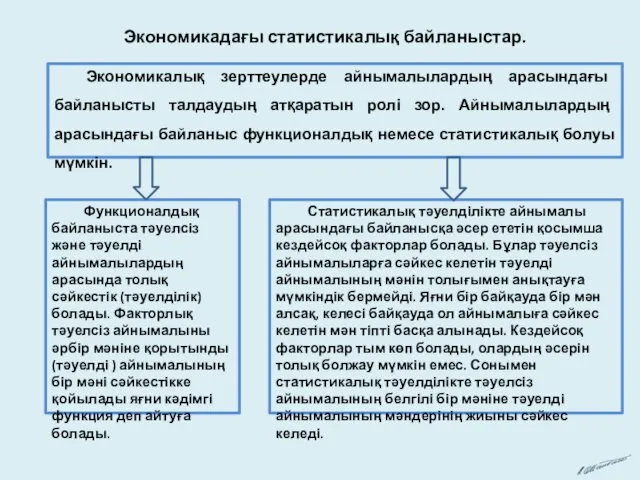 Экономикадағы статистикалық байланыстар
Экономикадағы статистикалық байланыстар Памятка по оформлению краткой записи к задачам
Памятка по оформлению краткой записи к задачам Квадратные неравенства
Квадратные неравенства Тема урока: знаки > (больше), < (меньше)Математика 1 класс Диск
Тема урока: знаки > (больше), < (меньше)Математика 1 класс Диск Алгоритмические структуры
Алгоритмические структуры Обчислення виду 13 + 2. Задачі різних типів з одним сюжетом. Урок №81
Обчислення виду 13 + 2. Задачі різних типів з одним сюжетом. Урок №81 Решение уравнений (6 класс)
Решение уравнений (6 класс) Утворення, запис, читання чисел
Утворення, запис, читання чисел Единицы массы: тонна и центнер
Единицы массы: тонна и центнер Понятие алгоритма действий
Понятие алгоритма действий Симметрия в пространстве. Симметрия в природе и на практике
Симметрия в пространстве. Симметрия в природе и на практике Урок -викторина Счастливый случай. Параллельные прямые
Урок -викторина Счастливый случай. Параллельные прямые Графическое решение квадратных уравнений
Графическое решение квадратных уравнений Разработка открытого урока математики
Разработка открытого урока математики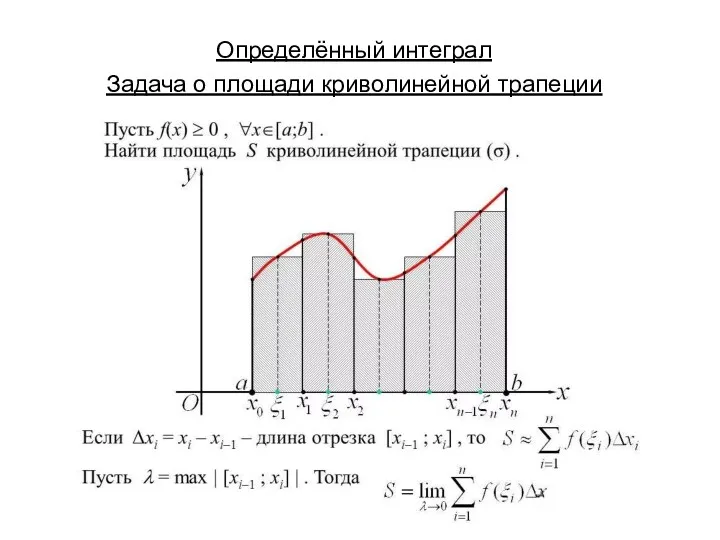 Определённый интеграл. Задача о площади криволинейной трапеции
Определённый интеграл. Задача о площади криволинейной трапеции Подготовка к ОГЭ. Методы, способствующие решению геометрических задач
Подготовка к ОГЭ. Методы, способствующие решению геометрических задач