Содержание
- 2. Активный эксперимент проводится по заранее составленному плану, в соответствии с которым ставится задача не только определения
- 3. Уравнения регрессии имеют следующий вид: вдали от экстремального значения выходной переменной у: вблизи экстремального значения выходной
- 4. Они включают слагаемые с двойным взаимодействием входных переменных и не учитывают взаимодействия более высоких порядков (тройные,
- 5. Полный факторный эксперимент Метод полного факторного эксперимента (ПФЭ) служит для получения математического описания процесса в виде
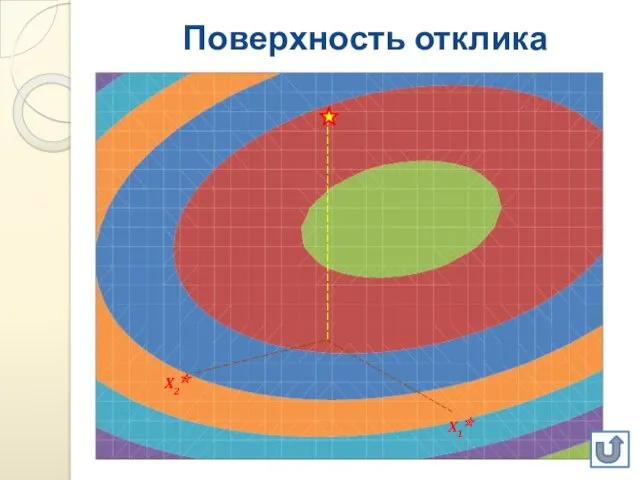
- 6. Поверхность отклика X2★ X1★
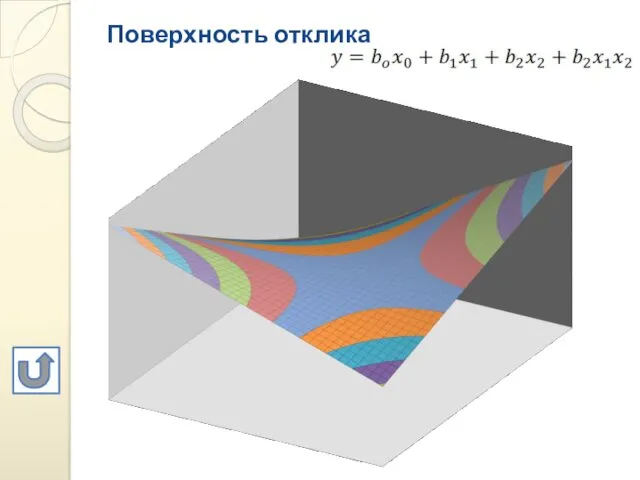
- 7. Поверхность отклика
- 8. Поверхность отклика
- 9. МАТРИЦА ПОЛНОГО ФАКТОРНОГО ЭКСПЕРИМЕНТА И ЕЁ СВОЙСТВА Полным факторным экспериментом называется система опытов, содержащая все возможные
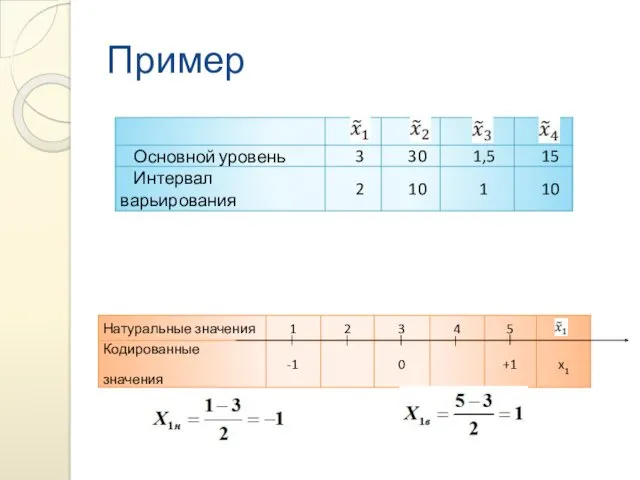
- 10. Для упрощения записи условий эксперимента и обработки экспериментальных данных пользуются кодированными переменными Переход к кодированным переменным
- 11. Пример
- 12. Общее число опытов ПФЭ определяется по формуле где k — число факторов План проведения экспериментов, называется
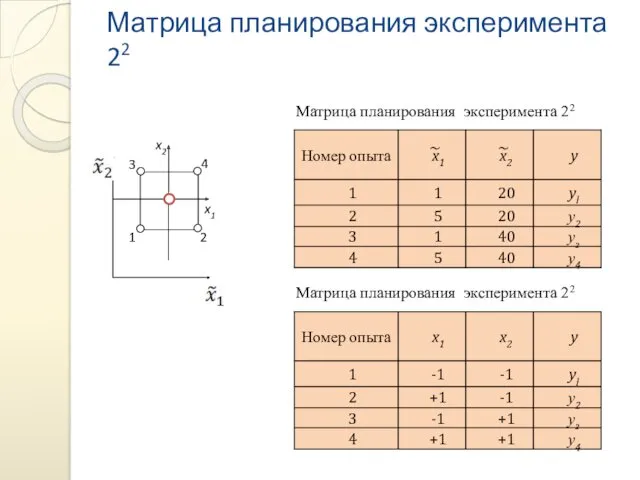
- 13. Матрица планирования эксперимента 22 ~ ~
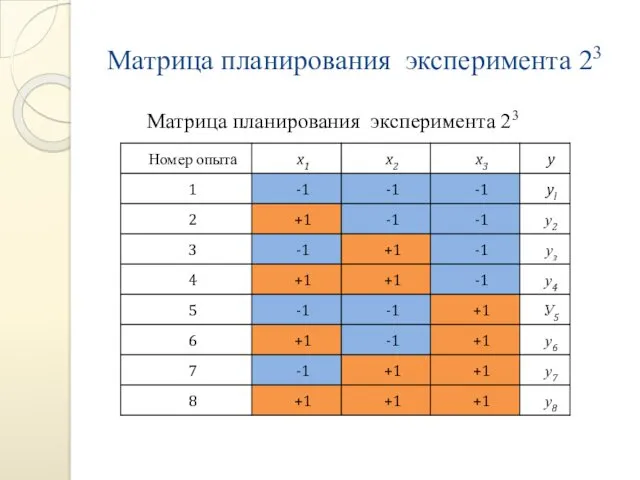
- 14. Матрица планирования эксперимента 23
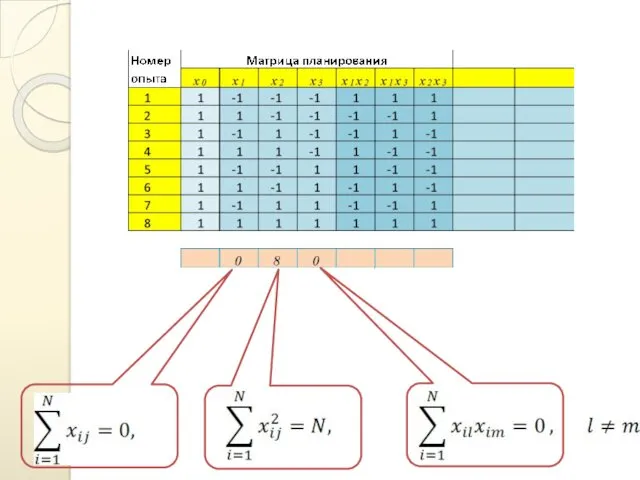
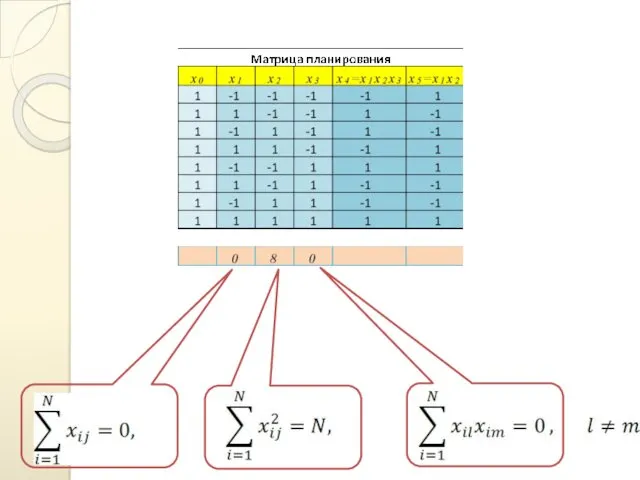
- 15. Матрица планирования ПФЭ обладает следующими свойствами: где i — номер опыта; j— номер фактора Свойство, выраженное
- 17. РАСЧЕТ КОЭФФИЦИЕНТОВ УРАВНЕНИЯ РЕГРЕССИИ Расчет коэффициентов регрессии для ПФЭ производится методом наименьших квадратов Благодаря свойствам матрицы
- 18. Проверка гипотезы о значимости коэффициентов уравнения регрессии производится с помощью критерия Стьюдента Проверка адекватности уравнения регрессии
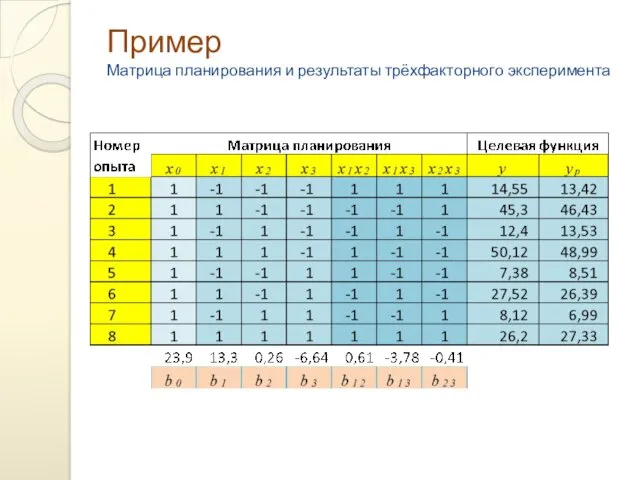
- 19. Пример Матрица планирования и результаты трёхфакторного эксперимента
- 20. ДРОБНЫЙ ФАКТОРНЫЙ ЭКСПЕРИМЕНТ Метод дробного факторного эксперимента (ДФЭ) предназначен для получения математического описания процесса в виде
- 21. Матрица дробного факторного эксперимента Одним из недостатков полного факторного эксперимента (ПФЭ) является то, что с увеличением
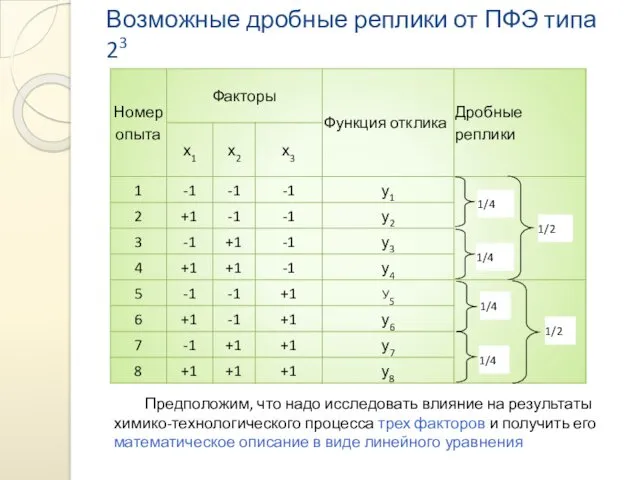
- 22. Возможные дробные реплики от ПФЭ типа 23 Предположим, что надо исследовать влияние на результаты химико-технологического процесса
- 23. Возьмем матрицу полного двухфакторного эксперимента и приравняем произведение х1х2 к фактору х3 По данному плану мы
- 24. Таким образом, сокращение числа опытов влечет за собой корреляцию между столбцами матрицы ДФЭ, что не позволяет
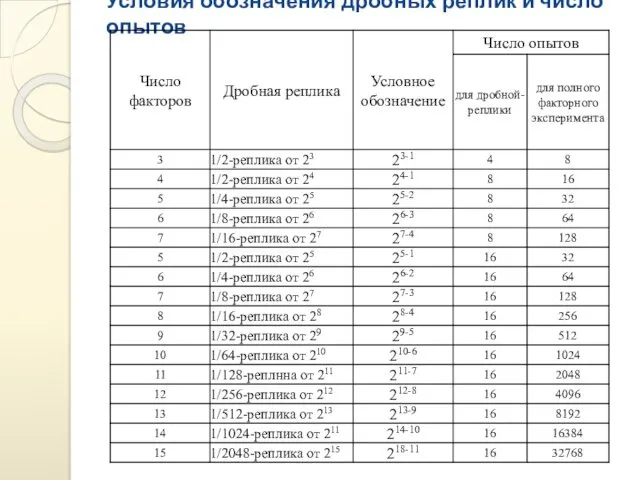
- 25. Условия обозначения дробных реплик и число опытов
- 26. ПЛАНИРОВАНИЕ СО СМЕШИВАНИЕМ. ОПРЕДЕЛЕНИЕ СОВМЕСТНЫХ ОЦЕНОК КОЭФФИЦИЕНТОВ РЕГРЕССИИ Планирование эксперимента, при котором некоторые из факторов приравниваются
- 27. Методом ДФЭ будем искать математическое описание процесса в виде уравнения регрессии Воспользуемся планированием типа 25-2 и
- 28. Перемножив почленно 1-й и 2-й определяющий контрасты, получим 1=(-x1x2x4)(x1x2x3x5) 1=-x3x4x5 Составим систему равенств из единицы и
- 29. Аналогично получим
- 30. РАЗРЕШАЮЩАЯ СПОСОБНОСТЬ МАТРИЦЫ ПЛАНИРОВАНИЯ Эффективность системы смешивания факторов и взаимодействий факторов определяется разрешающей способностью матрицы Она
- 31. Например, при выборе полуреплики типа 24-1 возможны 8 вариантов решений Наибольшая разрешающая способность у реплик 7-й
- 32. РАСЧЕТ КОЭФФИЦИЕНТОВ РЕГРЕССИИ Вычисление коэффициентов регрессии при использовании ДФЭ производится методом наименьших квадратов по формулам, которые
- 33. РАСЧЕТ КОЭФФИЦИЕНТОВ РЕГРЕССИИ В общем случае формулы для расчета коэффициентов регрессии по результатам ДФЭ имеют вид
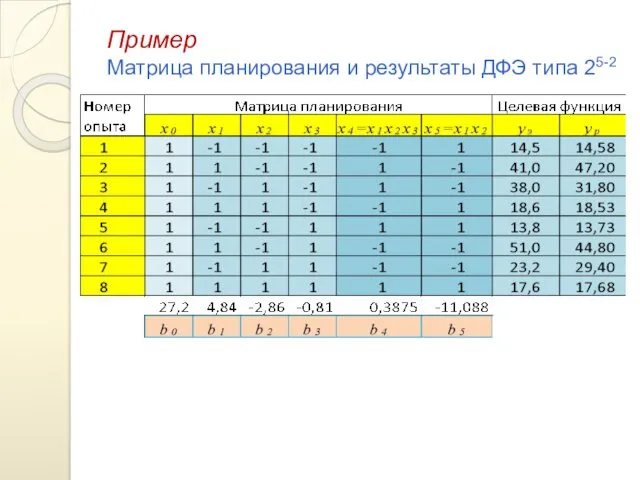
- 35. Пример Матрица планирования и результаты ДФЭ типа 25-2
- 36. ЭКСПЕРИМЕНТЫ НА ОСНОВЕ ПЛАНОВ ВТОРОГО ПОРЯДКА Планы второго порядка используют в тех случаях, когда функция отклика
- 37. Чтобы найти коэффициенты этого полинома, необходим эксперимент, в котором каждый фактор варьировался бы не менее чем
- 38. Исходя из этих соображений были разработаны так называемые композиционные планы второго порядка Структура данных планов представляет
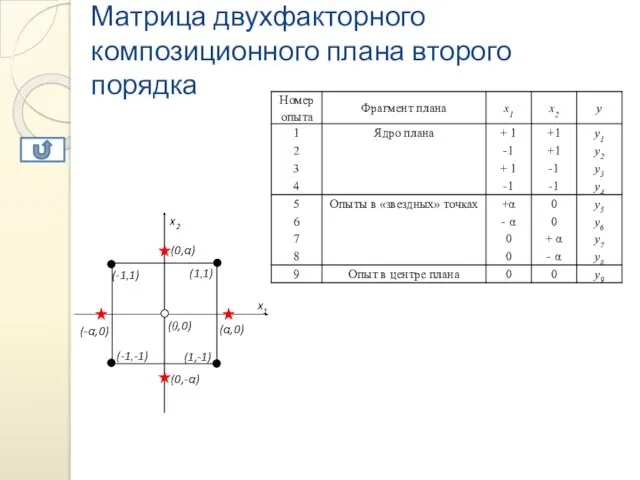
- 39. Матрица двухфакторного композиционного плана второго порядка
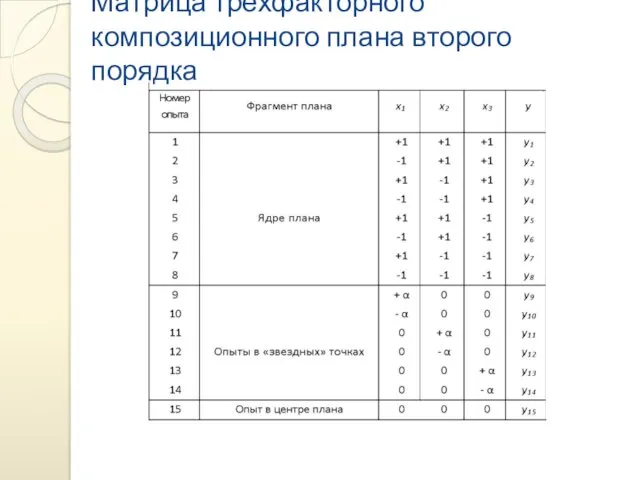
- 40. Матрица трехфакторного композиционного плана второго порядка
- 41. Если число факторов больше четырех, то в качестве ядра плана целесообразно использовать дробный факторный эксперимент Общее
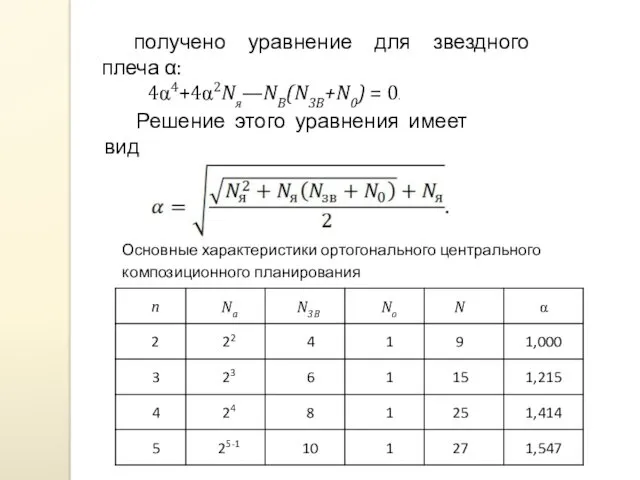
- 42. Известны два вида центрального композиционного планирования - ортогональное - ротатабельное
- 43. Ортогональное центральное композиционное планирование Свойство ортогональности его матрицы записывается следующим образом: т. е. сумма парных произведений
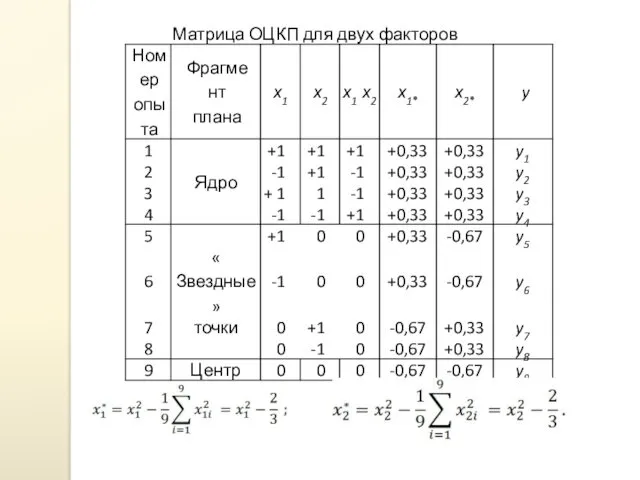
- 44. Например, для ОЦКП с двумя факторами имеем Для обеспечения ортогональности всех столбцов матрицы планирования вместо квадратов
- 45. получено уравнение для звездного плеча α: Решение этого уравнения имеет вид
- 48. Скачать презентацию






























 Объемные и плоские фигуры (1 класс)
Объемные и плоские фигуры (1 класс) Соавторская разработка развивающей презентации Что здесь лишнее? делопроизводителя Звягинцевой М.Ю. и воспитателя Авиловой Н.А.
Соавторская разработка развивающей презентации Что здесь лишнее? делопроизводителя Звягинцевой М.Ю. и воспитателя Авиловой Н.А. Урок математики во 2 классе
Урок математики во 2 классе Решение уравнений с десятичными дробями
Решение уравнений с десятичными дробями Деление с остатком
Деление с остатком Математическая смекалка. КВН
Математическая смекалка. КВН Разложение на простые множители
Разложение на простые множители Плоские и пространственные кривые. Поверхности. (Лекция 8)
Плоские и пространственные кривые. Поверхности. (Лекция 8) Свойства корня n-ой степени
Свойства корня n-ой степени Квадратный корень из дроби
Квадратный корень из дроби Геометрик фигураларны беләсеңме?
Геометрик фигураларны беләсеңме? Введение. Эконометрика и эконометрическое моделирование
Введение. Эконометрика и эконометрическое моделирование Тетраэдр, правильный многогранник
Тетраэдр, правильный многогранник Приёмы устных вычислений в пределах 1000. 3 класс
Приёмы устных вычислений в пределах 1000. 3 класс Introductory Statistics 1. AP Statistics
Introductory Statistics 1. AP Statistics Статистическое изучение взаимосвязей. Корреляционный и регрессионный анализ
Статистическое изучение взаимосвязей. Корреляционный и регрессионный анализ Математика. 1 класс. Урок 6. Признаки предметов
Математика. 1 класс. Урок 6. Признаки предметов Статистика в фармации. Корреляционный анализ
Статистика в фармации. Корреляционный анализ Математика 2 класс Диск
Математика 2 класс Диск Логарифмические неравенства
Логарифмические неравенства Третий признак равенства треугольников
Третий признак равенства треугольников Тесты по математике. Урок занимательной математики в 6 классе
Тесты по математике. Урок занимательной математики в 6 классе Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Сравнение отрезков и углов
Сравнение отрезков и углов Теория вероятностей и комбинаторные правила для решение задачи ЕГЭ В10. Новые прототипы
Теория вероятностей и комбинаторные правила для решение задачи ЕГЭ В10. Новые прототипы Промежутки возрастания и убывания функции
Промежутки возрастания и убывания функции Оценка устойчивости замкнутого контура САР по критерию Михайлова с помощью программы Exsel
Оценка устойчивости замкнутого контура САР по критерию Михайлова с помощью программы Exsel Решение заданий С1, С3
Решение заданий С1, С3