Содержание
- 2. Введение Если аргументы функции принимают только значения 0 или 1, то функция так же может принимать
- 3. Определение Алгебра логики – это исчисление булевых функций на основе тождеств.
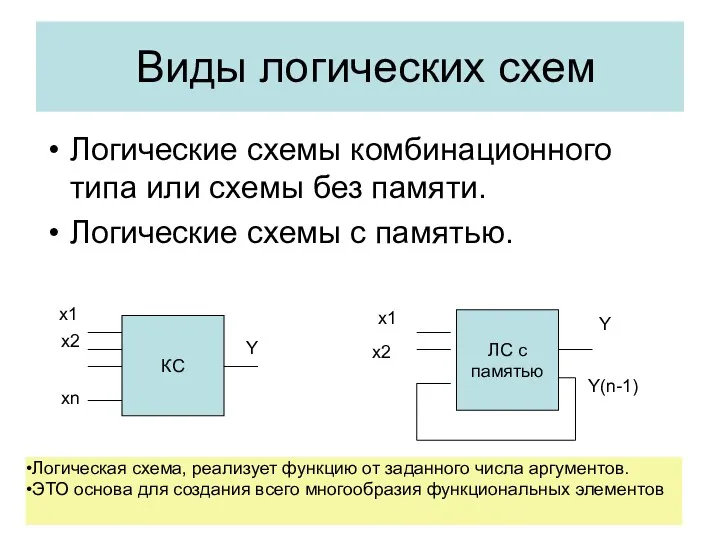
- 4. Виды логических схем Логические схемы комбинационного типа или схемы без памяти. Логические схемы с памятью. КС
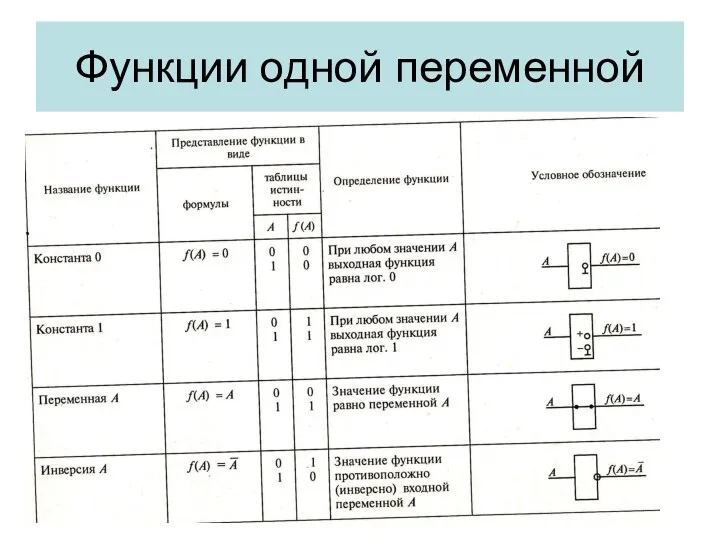
- 5. Функции одной переменной
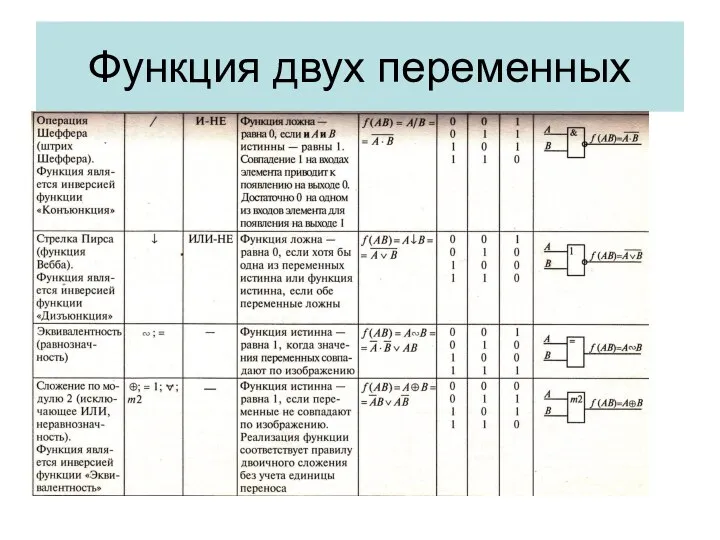
- 6. Функция двух переменных
- 7. Функция двух переменных
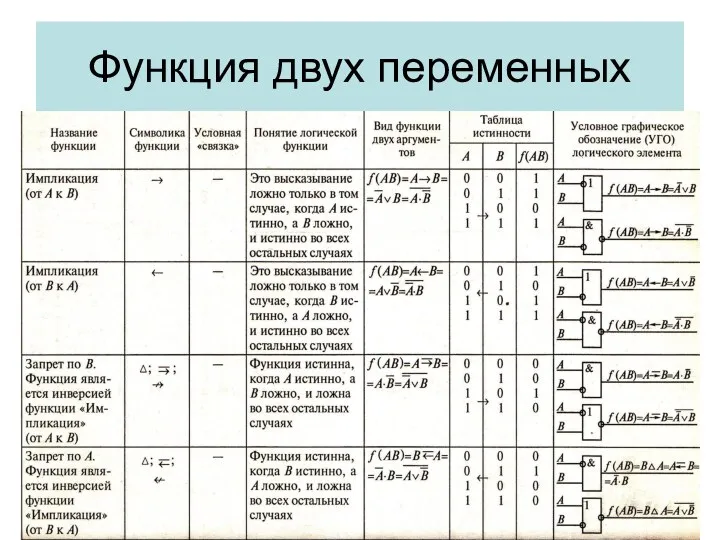
- 8. Функция двух переменных
- 9. Функциональное изображение логических элементов с двумя входами Основа для создания любой цифровой схемы Обычные логические выходы
- 10. Булевы тождества ВАЖНО. Одну и туже булеву функцию можно задать разными формулами. Это и есть тождества.
- 11. Тождества Коммутативные (переместительные) законы: Ассоциативные (сочетательные) законы:
- 12. Тождества Дистрибутивные (распределительные) законы: Законы повторения: Законы инверсии (двойственности):
- 13. Тождества Закон отрицания. Закон двойного отрицания. Закон поглощения. Закон склеивания.
- 14. Тождества их применение Операции с константами. и а а На доске привести ряд экспресс задач ……
- 15. Сводный список тождеств ЗАДАЧА. Дайте графическую интерпретацию этих тождеств
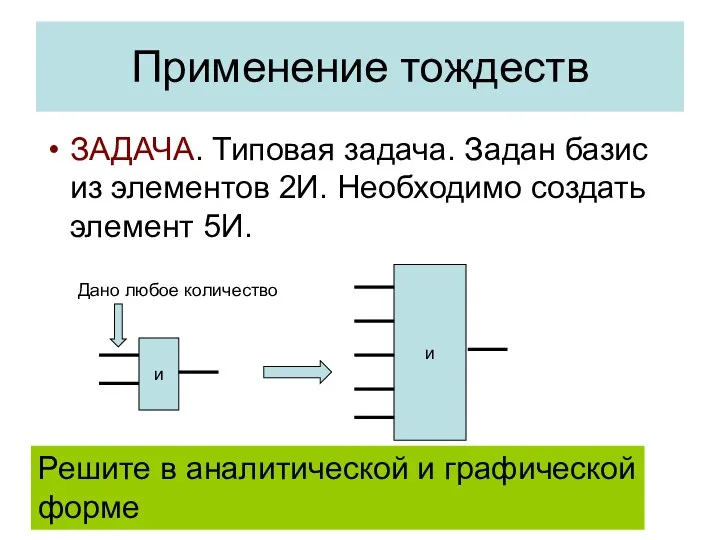
- 16. Применение тождеств ЗАДАЧА. Типовая задача. Задан базис из элементов 2И. Необходимо создать элемент 5И. и и
- 17. Используется для перехода от одного логического базиса к другому. ЗАДАЧА. Задан базис элементов 2И-НЕ. Постройте из
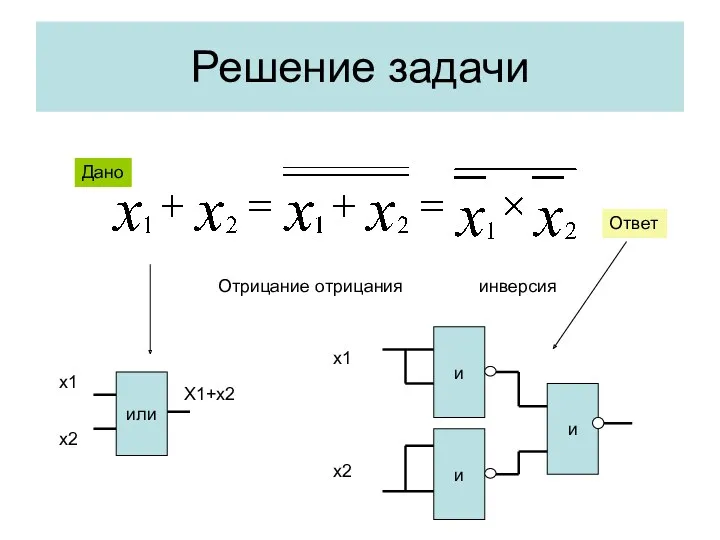
- 18. Решение задачи Отрицание отрицания инверсия или х1 х2 Х1+х2 и и и х1 х2 Ответ Дано
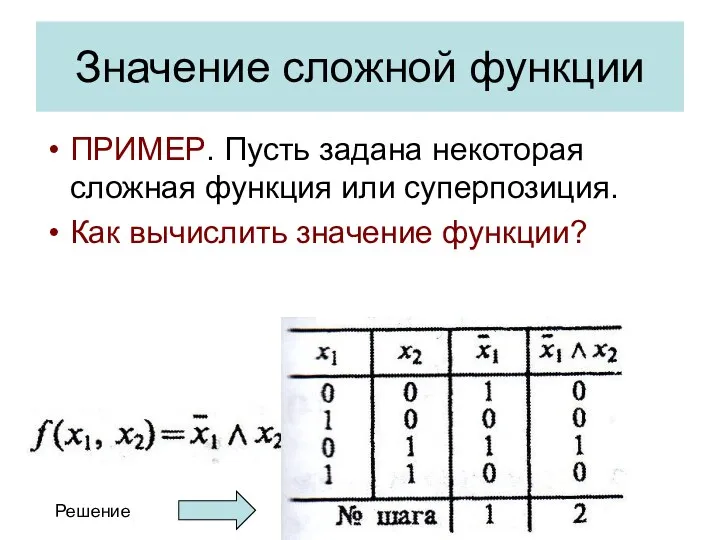
- 19. Значение сложной функции ПРИМЕР. Пусть задана некоторая сложная функция или суперпозиция. Как вычислить значение функции? Решение
- 20. Пример 2. Вычислить значение функции. Значение сложной функции Из этой методики следует важное следствие
- 21. Логические выражения и логические схемы Задача. По формуле составьте изображение логической схемы
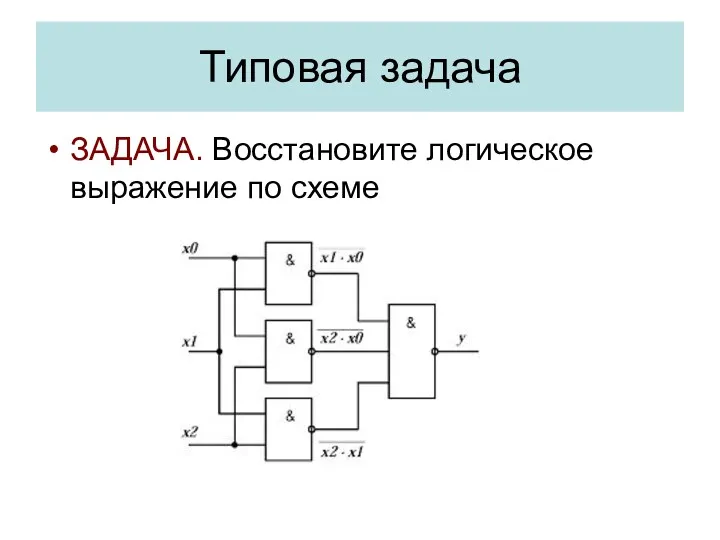
- 22. Типовая задача ЗАДАЧА. Восстановите логическое выражение по схеме
- 23. Булева функция N переменных ТЕОРЕМА. Любую булеву функцию n переменных можно задать с помощью формулы, употребляя
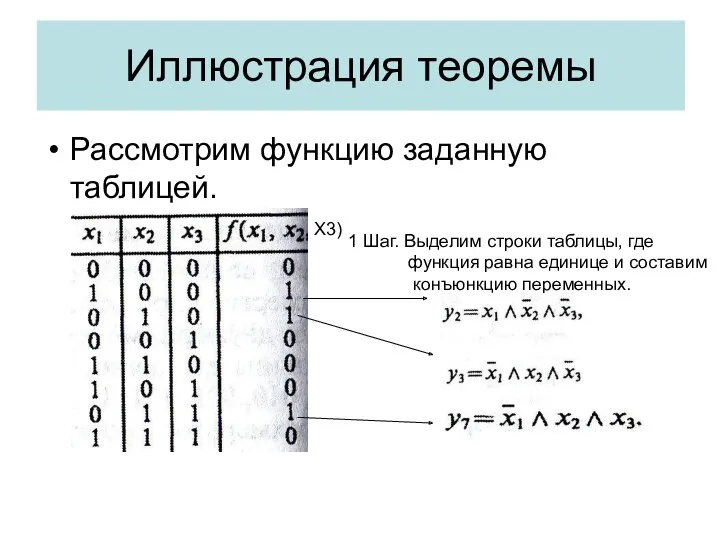
- 24. Иллюстрация теоремы Рассмотрим функцию заданную таблицей. 1 Шаг. Выделим строки таблицы, где функция равна единице и
- 25. Шаг 2. Строим дизъюнкцию построенных конъюнкций. Продолжение иллюстрации теоремы Функция стоящая в правой части равенства называется
- 26. Дизъюнктивная и конъюнктивная нормальные формы представления функций в алгебре логики Чтобы знать переключательную функцию, необязательно задавать
- 27. Определения Произведение переменных, в которое каждая из переменных входит только один раз в прямом или инверсном
- 28. Минтерм, макстерм, ранг Количество переменных, входящих в минтерм и макстерм, называется рангом
- 29. Пример Задана функция от двух переменных, как будут выглядеть минтермы и макстермы этой функции.
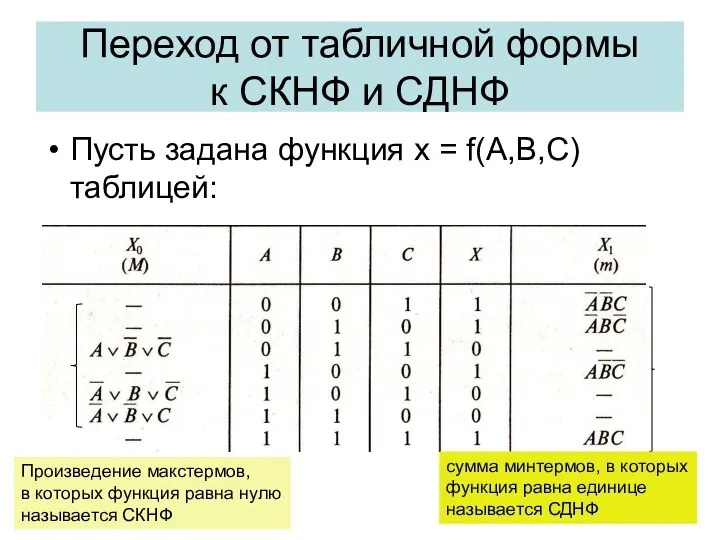
- 30. Переход от табличной формы к СКНФ и СДНФ Пусть задана функция х = f(А,B,C) таблицей: сумма
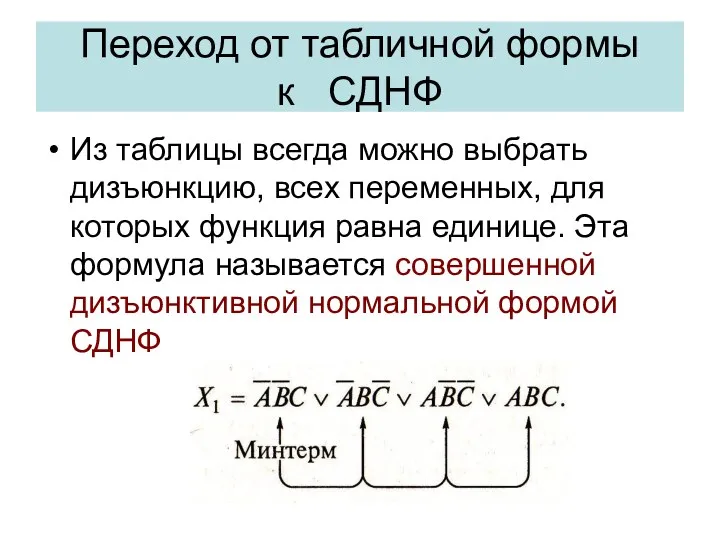
- 31. Из таблицы всегда можно выбрать дизъюнкцию, всех переменных, для которых функция равна единице. Эта формула называется
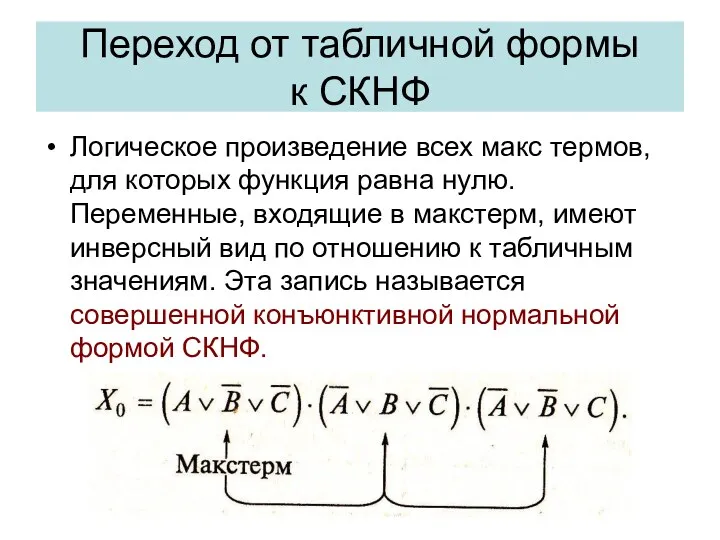
- 32. Логическое произведение всех макс термов, для которых функция равна нулю. Переменные, входящие в макстерм, имеют инверсный
- 34. Скачать презентацию



















 Урок математики Решение уравнений 3 класс УМК Школа России
Урок математики Решение уравнений 3 класс УМК Школа России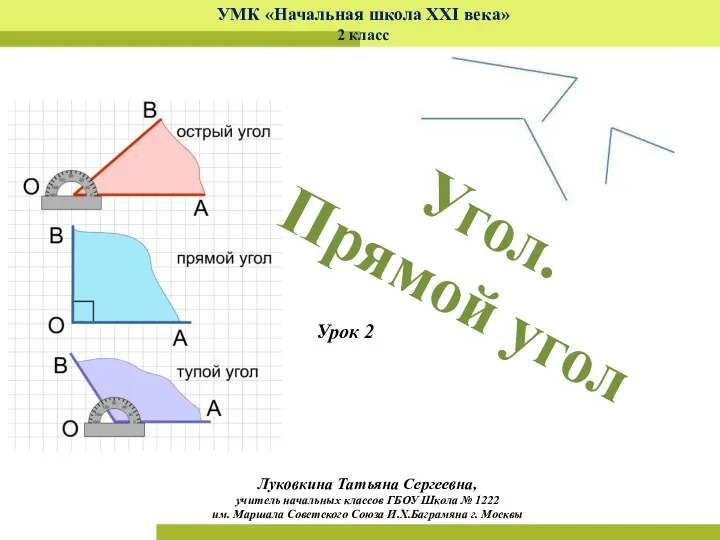 Угол. Прямой угол
Угол. Прямой угол Простейшие задачи в координатах (9 класс)
Простейшие задачи в координатах (9 класс) Тест. Задания В8, ЕГЭ по математике
Тест. Задания В8, ЕГЭ по математике Медианы, биссектрисы и высоты треугольника
Медианы, биссектрисы и высоты треугольника Случайные величины, законы их распределения и числовые характеристики
Случайные величины, законы их распределения и числовые характеристики Куб (текше) және оның көлемі
Куб (текше) және оның көлемі Множество значений функции (+ презентация)
Множество значений функции (+ презентация) Объем цилиндра и призмы
Объем цилиндра и призмы Числовые неравенства и их свойства
Числовые неравенства и их свойства Обратная матрица. (Тема 7)
Обратная матрица. (Тема 7) 4 класс задача на движение
4 класс задача на движение Площади плоских фигур
Площади плоских фигур История возникновения нуля, его значение в жизни человека
История возникновения нуля, его значение в жизни человека Законы арифметических действий
Законы арифметических действий Луч и угол. 7 класс
Луч и угол. 7 класс Показательная функция и её применение
Показательная функция и её применение Зеркальное отражение предметов.1 класс
Зеркальное отражение предметов.1 класс Меры длины
Меры длины Презентация по геометрии по теме Теорема синусов, теорема косинусов 9 класс
Презентация по геометрии по теме Теорема синусов, теорема косинусов 9 класс методическая разработка урока математики Единицы времени.Век
методическая разработка урока математики Единицы времени.Век Смотр знаний по теме Дробные числа 5 класс
Смотр знаний по теме Дробные числа 5 класс Способы разложения многочлена на множители
Способы разложения многочлена на множители Урок математики. (Часть 2. 1 класс)
Урок математики. (Часть 2. 1 класс) Арифметические действия с числами. Задания для устного счета. 6 класс
Арифметические действия с числами. Задания для устного счета. 6 класс Статистика
Статистика Внетабличное умножение и деление. Памятники Кремля.3 класс
Внетабличное умножение и деление. Памятники Кремля.3 класс Дециметр. Предложение
Дециметр. Предложение