Слайд 2

Учебные вопросы
1. Введение в теорию ДУ:
задачи, приводящие к понятию дифференциального
уравнения.
2.Обыкновенные дифференциальные уравнения, основные понятия (порядок, степень, решение). 3.Дифференциальные уравнения первого порядка.
Слайд 3

4. Частное и общее решения, интегральные кривые, поле направлений.
5. Интегрирование
уравнений с разделяющимися переменными.
Слайд 4
![Литература [2] Н.С. Пискунов. Дифференциальное и интегральное исчисления. Т 2.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/94364/slide-3.jpg)
Литература
[2] Н.С. Пискунов. Дифференциальное и интегральное исчисления. Т 2. Москва: Интеграл-Пресс,
2005. с. 13-90;
[3] Б.П. Демидович, В.А. Кудрявцев. Краткий курс высшей математики. Москва: Издательство АСТ, 2004. с. 446-490.
Слайд 5

1.Задачи, приводящие к понятию дифференциального уравнения.
Задача 1.
На плоскости XOY
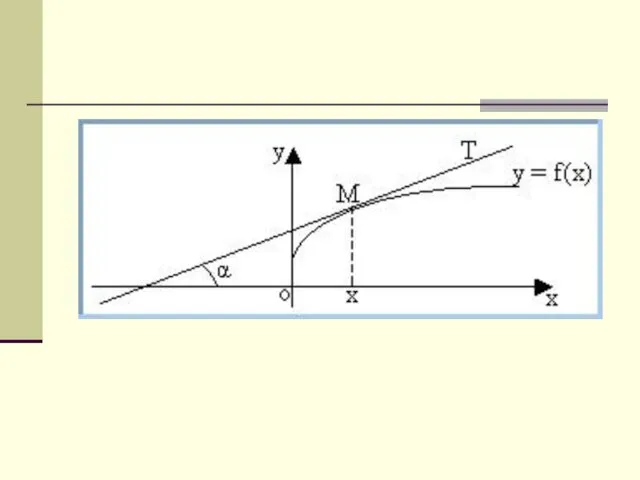
найти кривую, которая в каждой своей точке имеет касательную, образующую с положительным направлением оси Ox угол, тангенс которого равен удвоенной абсциссе точки касания.
Решение.
Пусть уравнение искомой кривой y=f(x).
Слайд 6
Слайд 7

Угловой коэффициент касательной МТ есть tgα, он равен производной от y
по x, так что
С другой стороны, по условию задачи имеем
.
Приравнивая значения tg α, получим
Слайд 8

Решением дифференциального уравнения является любая первообразная для функции 2x. Например,
решением
будет .
Слайд 9

Все первообразные для функции 2x и, следовательно, все решения дифференциального
уравнения задаются формулой
.
Слайд 10

Дифференциальное уравнение имеет бесчисленное множество решений.
Слайд 11

Но если в условие задачи добавить точку M0 (x0, y0), через
которую проходит искомая кривая, то получим единственную кривую.
Слайд 12

Для этого достаточно заменить в уравнении координаты x и y координатами
точки M0
Слайд 13

Отсюда имеем и
Таким образом, искомой кривой будет парабола.
Слайд 14

Задача 2.
Допустим, что в каждый момент времени t известна скорость v(t)
точки, движущейся по оси OX, где v(t) - функция, непрерывная на (a,b).
Слайд 15

Кроме того, известно значение х0 положения точки в определенный момент времени
t0 . Требуется найти закон движения точки.
Слайд 16

Решение.
Положение точки определяется одной координатой х и задача состоит в том,
чтобы выразить х как функцию от t . Принимая во внимание механический смысл первой производной, мы получим равенство
Слайд 17

Как известно из интегрального исчисления
Слайд 18

Так как в формулу входит произвольная постоянная C, то мы ещё
не получили определённого закона движения точки.
Слайд 19

Поскольку движущаяся точка принимает положение х0 в заданный момент времени t0,
то
Слайд 20
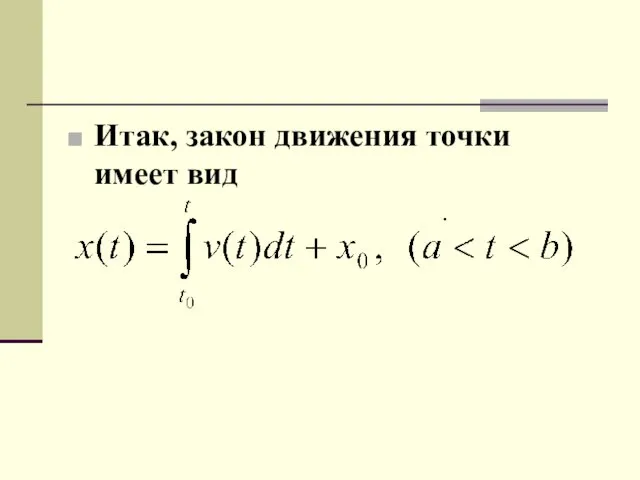
Итак, закон движения точки имеет вид
.
Слайд 21

Учебный вопрос.
Обыкновенные дифференциальные уравнения, основные понятия (порядок, степень, решение).
Слайд 22

ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, ОСНОВНЫЕ ПОНЯТИЯ.
Определение. Обыкновенным дифференциальным уравнением n–ого порядка называется
выражение вида:
где х – независимая переменная;
у(х) – неизвестная функция;
– производные искомой функции.
Слайд 23

Определение. Порядком n дифферен-циального уравнения называется порядок наивысшей производной, входящей в
это уравнение.
Например,
Слайд 24

Определение. Решением дифференциального уравнения называется функция у=φ(х), которая при подстановке в
уравнение обращает его в верное равенство.
Слайд 25

Определение. График решения дифференциального уравнения называется интегральной кривой дифференциального уравнения.
Процесс
нахождения решения дифференциального уравнения называется интегрированием этого уравнения.
Слайд 26

Определение. Решение дифференциального уравнения, полученное в неявном виде
,
называется
интегралом дифференциального уравнения.
Слайд 27

Учебный вопрос.
Дифференциальные уравнения первого порядка.
Слайд 28

Дифференциальные уравнения первого порядка.
Определение. Дифференциальным уравнением первого порядка называется соотношение, связывающее
независимую переменную, искомую функцию и ее первую производную: ,
где
Слайд 29

Если уравнение разрешить относительно производной , то получим
уравнение нормального
вида:
Слайд 30

Учебный вопрос.
ЧАСТНОЕ И ОБЩЕЕ РЕШЕНИЯ, ИНТЕГРАЛЬНЫЕ КРИВЫЕ, ПОЛЕ НАПРАВЛЕНИЙ
Слайд 31

ЧАСТНОЕ И ОБЩЕЕ РЕШЕНИЯ, ИНТЕГРАЛЬНЫЕ КРИВЫЕ, ПОЛЕ НАПРАВЛЕНИЙ
Определение. Решение у=φ(х,С),
которое зависит от независимой переменной х и произвольной постоянной, называется общим решением ДУ первого порядка.
Слайд 32

Решение у=φ(х), полученное из общего при фиксированном значении произвольной постоянной, называется
частным решением ДУ первого порядка.
Слайд 33

Задача Коши для уравнения
состоит в том, чтобы найти частное решение уравнения,
удовлетворяющее начальному условию
Слайд 34

Уравнение
в каждой точке
M (x , y) области, где
определено его решение у=φ(х ,С ),
задаёт направление касательной к интегральной кривой. В итоге мы получаем целое поле направлений.
Слайд 35

Это поле графически можно изобразить, поместив в каждой точке M(x, y)
черточку, наклоненную к оси Ox под углом, тангенс которого равен
Слайд 36

Слайд 37

ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ
Определение. ДУ первого порядка называется уравнением
с разделенными переменными, если его можно представить в виде
Слайд 38

Слайд 39

Пример. Найти общее решение дифференциального уравнения
Решение.
Слайд 40
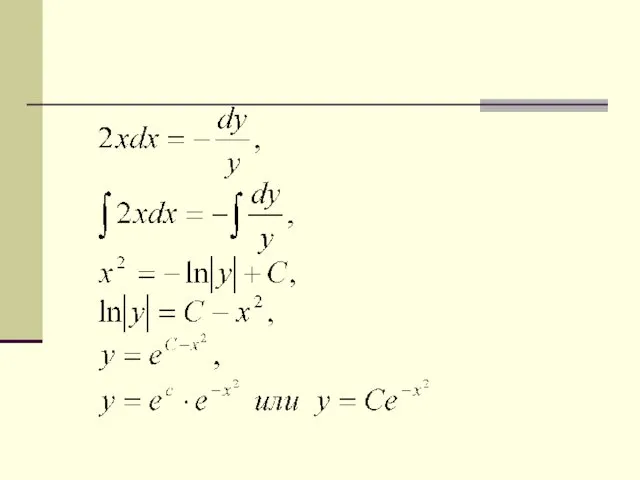
Слайд 41

Определение. Уравнение вида
называется уравнением с разделяющимися переменными.
Слайд 42

В этом уравнении легко разделить переменные. Для этого поделим уравнение на
произведение
. Тогда получим
- это уравнение с разделенными переменными.
Слайд 43

Слайд 44

ЗАМЕЧАНИЕ
Мы могли потерять некоторые решения, которые обращают в нуль произведение R(x)Q(y),
а именно Q(y)=0, отсюда yk= ak ,где ak – const.
Слайд 45

Если решения yk= ak получаются из общего при подходящем выборе С,
то такие решения будут частными, если же подобрать нужное С невозможно, то они называются особыми решения.
Слайд 46

Пример.
Найти общий интеграл и частное решение уравнения
удовлетворяющее условию .
Решение.
Делим
на ,
тогда
Слайд 47

Слайд 48

-общий интеграл.
Подставим начальное условие и найдем С:
.
Слайд 49

Частное решение
Особое решение
так как
Слайд 50

Учебные вопросы
6. Однородные и линейные уравнения 1 порядка.
7. Уравнения Бернулли
1-го порядка.
8. Дифференциальные уравнения высших порядков, начальные и граничные условия.
Слайд 51

Учебный вопрос.
Однородные и линейные уравнения 1 порядка.
Слайд 52

Однородные уравнения 1-го порядка.
Определение. Дифференциальеное уравнение 1 порядка называется однородным
ДУ-1, если f(x,y) может быть представлена как функция отношения своих аргументов,
т.е. или
f(λx,λy)=f(x,y), где λ – const.
Слайд 53

1) Однородные уравнения приводятся к уравнениям с разделяющимися переменными
с
помощью следующей замены: , т.е.
у=zх, отсюда у’=z’x+z .
2) После подстановки у, у’ в исходное уравнение получим ДУ с разделяющимися переменными, в котором неизвестной является функция z(x).
3)После интегрирования в общем решении необходимо z заменить на отношение .
Слайд 54

Пример
Решить уравнение ху+ y2 = (2х2 +ху)у’ .
Решение.
Слайд 55

Слайд 56

Слайд 57

Линейные уравнения первого порядка
Определение. Линейным дифференциальным уравнением 1-го порядка называется уравнение
вида:
,
где у(х) – неизвестная функция.
Это уравнение линейно относительно у и у’ .
Если правая часть уравнения q(x) = 0, то получим уравнение
,
которое называется линейным однородным, соответствующим линейному неоднородному уравнению.
Слайд 58

Рассмотрим линейное уравнение Неизвестную функцию у(х) будем искать в виде произведения
неизвестных функций
у(х)=u(x)∙v(x), тогда y’=u’v+uv’. Подставляя y и y’ в исходное уравнение, получим:
Слайд 59

Положим и найдем функцию v(x), решая это уравнение с разделяющи-мися переменными:
Слайд 60

Для нахождения u(x) подставим найденную функцию v(x) и ее производную
=
в
уравнение, получим уравнение с разделяющимися переменными
.
Решим его
Слайд 61

Слайд 62

Пример
Найти частное решение, удовлетворяющее заданному начальному условию
Слайд 63

Слайд 64

Слайд 65

Следовательно, частное решение данного дифференциального уравнения имеет вид:
у = .
Слайд 66

Учебный вопрос.
Уравнения Бернулли.
Слайд 67

Уравнения Бернулли.
Определение. Дифференциальное уравнение вида , где α ≠ 0,
1
называется уравнением Бернулли.
1)Предполагая, что у ≠ 0, разделим обе части уравнения Бернулли на уα. В результате получим:
Слайд 68

2) Введем новую функцию . Тогда
3) Умножим уравнение на (-α+1)
и перейдем в нем к функции z(x):
Слайд 69

4)Получили линейное неоднородное уравнение
1-го порядка. Это уравнение решается методом
множителей Бернулли.
5)Решив уравнение , подставим в его общее решение вместо z(x) выражение , получим общий интеграл уравнения Бернулли.
Уравнение Бернулли можно также решить, не делая замены переменных, а сразу применяя метод множителей Бернулли.
Слайд 70

Пример
Найти общее решение уравнения
Решение.
Слайд 71

Слайд 72

Дифференциальные уравнения высших порядков, начальные и граничные условия.
Слайд 73

Дифференциальные уравнения высших порядков, начальные и граничные условия.
Определение. Уравнением n-го порядка
называется уравнение вида
, (n>1) .
Задача Коши уравнения n-го порядка ставится следующим образом: найти решение y=y(x) удовлетворяющее начальным условиям
Слайд 74

Определение. Общим решением ДУ n-го порядка называется функция y=φ(x,C1,C2,…,Cn), которая при
подстановке в уравнение обращает его в верное равенство.
Слайд 75
![Задание на самостоятельную работу Вспомнить таблицу основных интегралов. [2] Н.С.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/94364/slide-74.jpg)
Задание на самостоятельную работу
Вспомнить таблицу основных интегралов.
[2] Н.С. Пискунов. Дифференциальное и
интегральное исчисления. Т 2. Москва: Интеграл-Пресс, 2005. с. 13-90;
[3] Б.П. Демидович, В.А. Кудрявцев. Краткий курс высшей математики. Москва: Издательство АСТ, 2004. с. 446-490.


![Литература [2] Н.С. Пискунов. Дифференциальное и интегральное исчисления. Т 2.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/94364/slide-3.jpg)


































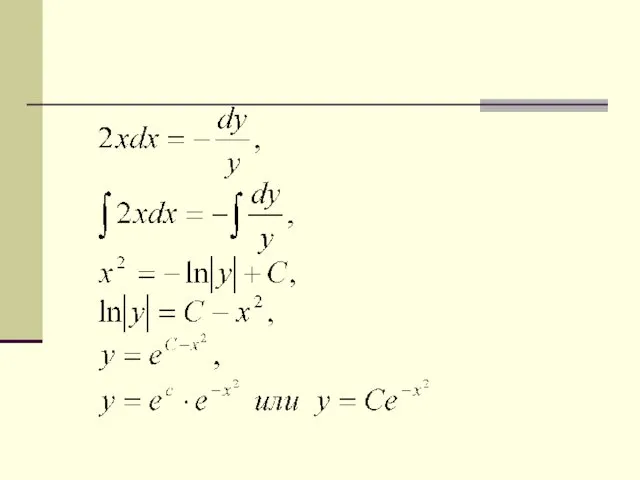


































![Задание на самостоятельную работу Вспомнить таблицу основных интегралов. [2] Н.С.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/94364/slide-74.jpg)
 Тоновое решение, акценты эскизов. Линия, пятно и линия, пятно
Тоновое решение, акценты эскизов. Линия, пятно и линия, пятно Язык геометрических рисунков
Язык геометрических рисунков Пропорциональные отрезки в прямоугольном треугольнике
Пропорциональные отрезки в прямоугольном треугольнике Определённый интеграл. Свойства определённого интеграла
Определённый интеграл. Свойства определённого интеграла Математический КВН
Математический КВН Свойства умножения (4 класс).
Свойства умножения (4 класс). Неравенства и системы неравенств с двумя переменными
Неравенства и системы неравенств с двумя переменными Сложение и вычитание вида 10+7, 17-7, 17-10
Сложение и вычитание вида 10+7, 17-7, 17-10 Наука геометрия
Наука геометрия Правильные многоугольники
Правильные многоугольники Discrete random variables – expected variance and standard deviation. Discrete Probability Distributions. Week 7 (1)
Discrete random variables – expected variance and standard deviation. Discrete Probability Distributions. Week 7 (1) Теорема Пифагор
Теорема Пифагор Занимательные задачи в курсе математики 5-6 классов
Занимательные задачи в курсе математики 5-6 классов Построение сечения многогранника плоскостью
Построение сечения многогранника плоскостью Ch8: Hypothesis Testing (2 Samples)
Ch8: Hypothesis Testing (2 Samples) Геометрия на клетчатой бумаге. Теорема Пика
Геометрия на клетчатой бумаге. Теорема Пика Как определить площадь многоугольника, изображенного на клетчатой основе
Как определить площадь многоугольника, изображенного на клетчатой основе Решение сложных уравнений (4 класс)
Решение сложных уравнений (4 класс) Корень n-й степени из числа а. 10 класс
Корень n-й степени из числа а. 10 класс Движения
Движения Решение задач на вписанные и описанные многогранники (пирамида)
Решение задач на вписанные и описанные многогранники (пирамида) Линейные операции над векторами. Базис и координаты
Линейные операции над векторами. Базис и координаты Свойства квадратных корней
Свойства квадратных корней Решение задач на проценты (5 класс)
Решение задач на проценты (5 класс) Веселая математика
Веселая математика Ремонт кабинета с использованием математических формул
Ремонт кабинета с использованием математических формул Решение задач с параметром графическими методами
Решение задач с параметром графическими методами Деление на двузначное число
Деление на двузначное число