Содержание
- 2. Функции а л г е б р ы л о г и к и Переменные xi,
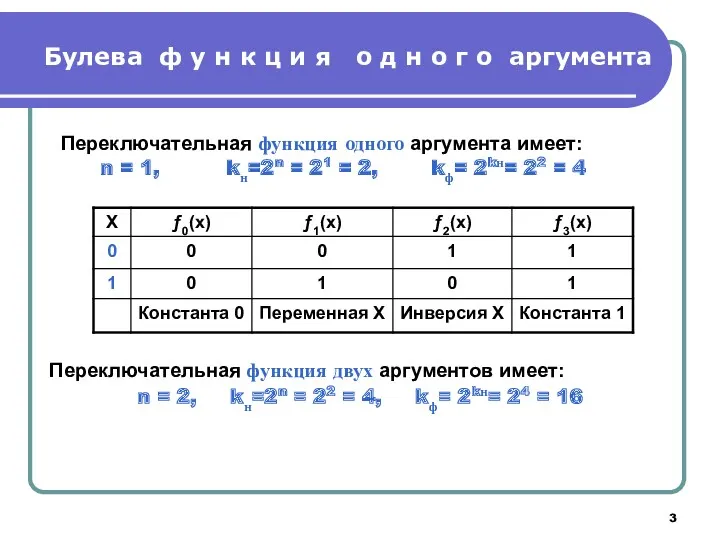
- 3. Булева ф у н к ц и я о д н о г о аргумента Переключательная
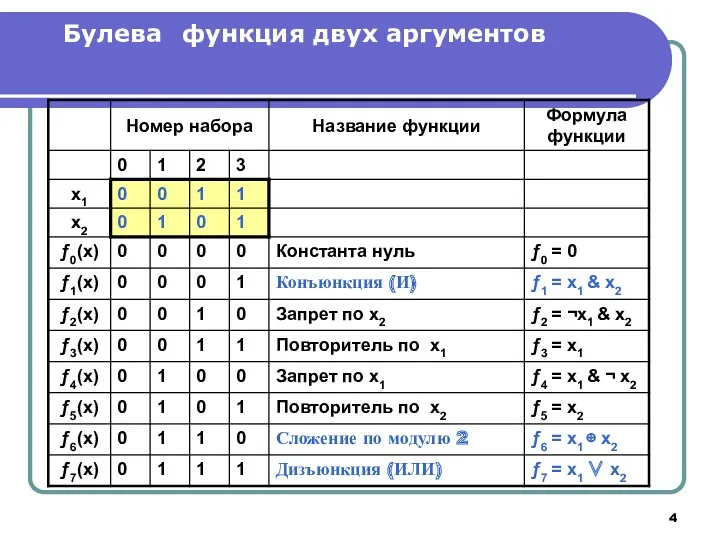
- 4. Булева функция двух аргументов
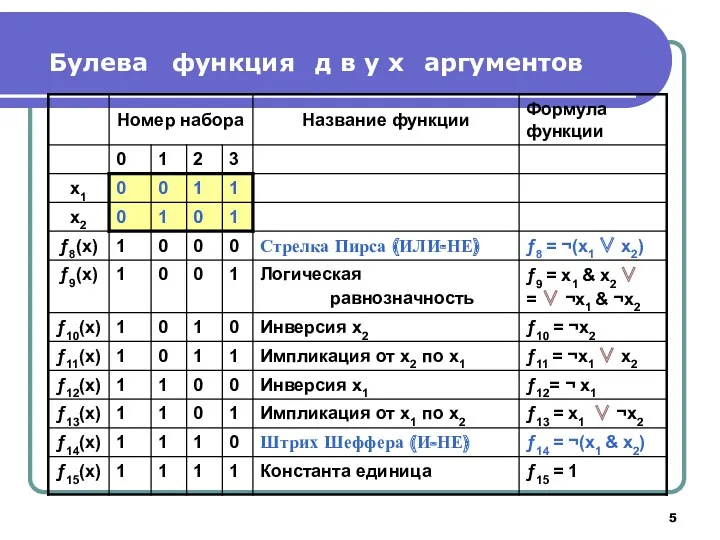
- 5. Булева функция д в у х аргументов
- 6. Функционально п о л н ы й набор На практике используют не все функции, а только
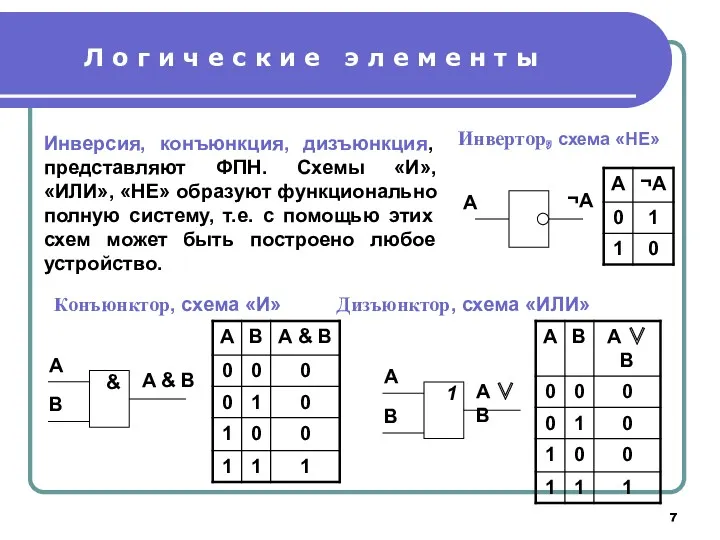
- 7. Л о г и ч е с к и е э л е м е н
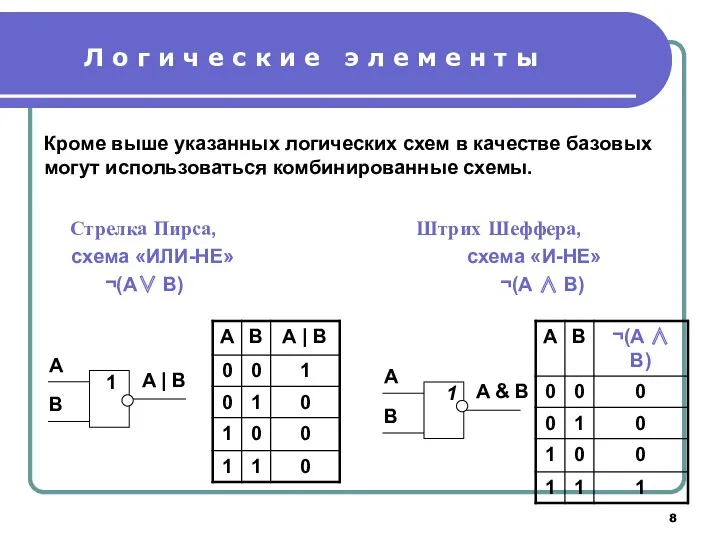
- 8. Л о г и ч е с к и е э л е м е н
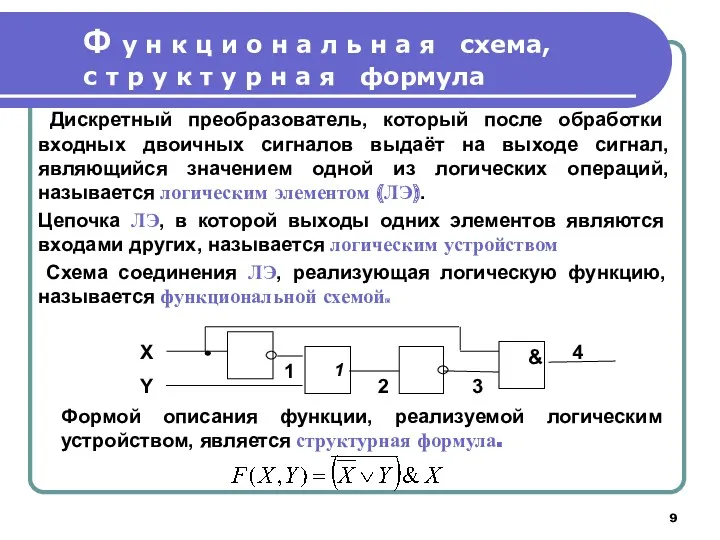
- 9. Дискретный преобразователь, который после обработки входных двоичных сигналов выдаёт на выходе сигнал, являющийся значением одной из
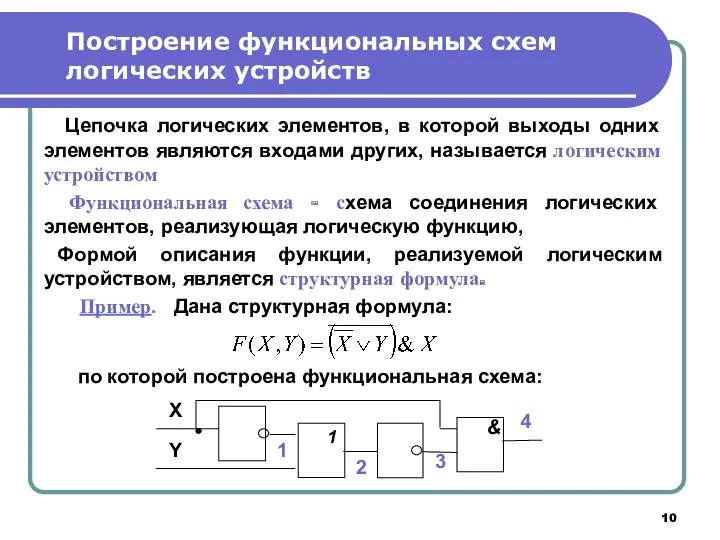
- 10. Цепочка логических элементов, в которой выходы одних элементов являются входами других, называется логическим устройством Функциональная схема
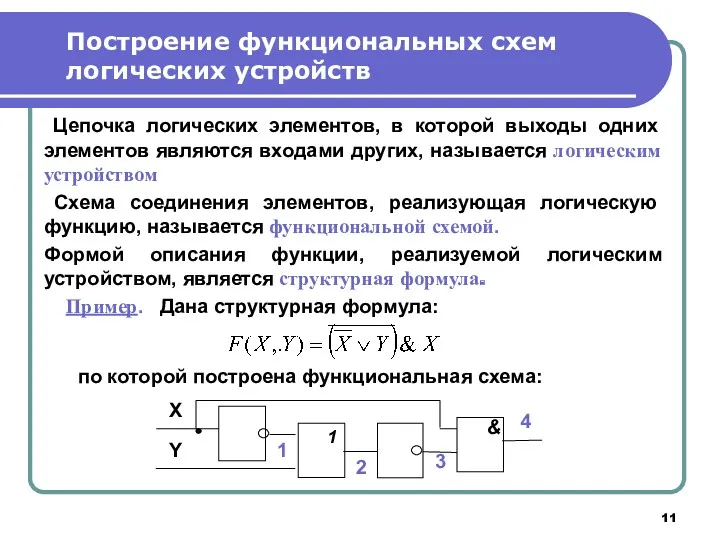
- 11. Цепочка логических элементов, в которой выходы одних элементов являются входами других, называется логическим устройством Схема соединения
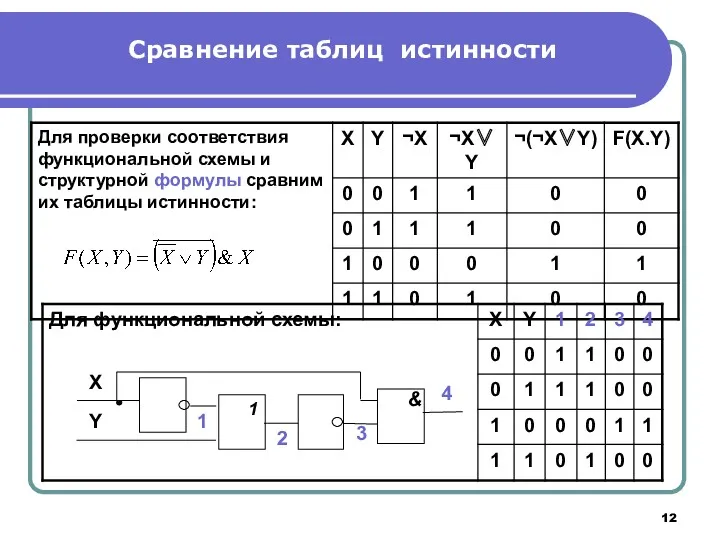
- 12. Сравнение таблиц истинности
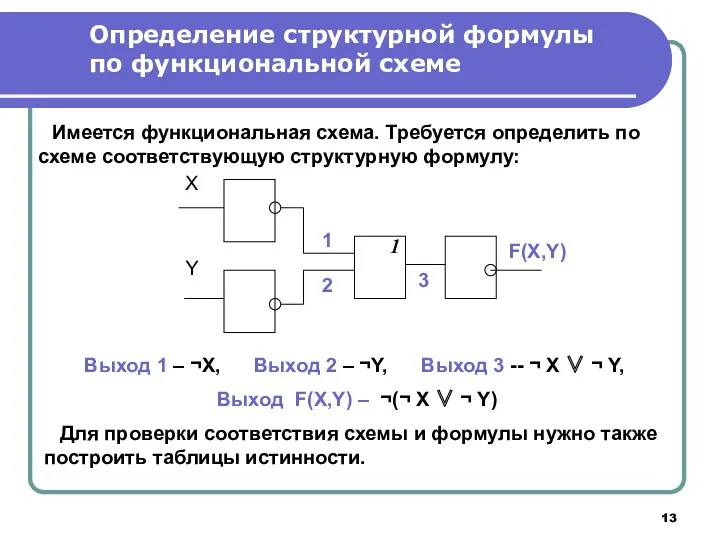
- 13. Определение структурной формулы по функциональной схеме Имеется функциональная схема. Требуется определить по схеме соответствующую структурную формулу:
- 14. Дизъюнктивная нормальная форма и конъюнктивная нормальная форма Элементарная конъюнкция – логическое произведение (конъюнкция) аргументов или их
- 15. Совершенная дизъюнктивная нормальная форма и совершенная конъюнктивная нормальная форма Совершенной дизъюнктивной нормальной формой (СДНФ) называется ДНФ,
- 16. А л г о р и т м п о л у ч е н и
- 18. Скачать презентацию





 Симметрия в природе
Симметрия в природе Викторина По страницам школьных учебников. Математика – царица наук
Викторина По страницам школьных учебников. Математика – царица наук Решение задач на увеличение и уменьшение в несколько раз
Решение задач на увеличение и уменьшение в несколько раз Приближенное решение алгебраических и трансцендентных уравнений. Решение уравнений с одной переменной. Лекция 5
Приближенное решение алгебраических и трансцендентных уравнений. Решение уравнений с одной переменной. Лекция 5 Елементи комбінаторики
Елементи комбінаторики Статистическое наблюдение
Статистическое наблюдение Смешанные числа
Смешанные числа Случайные величины
Случайные величины Ломаная Диск
Ломаная Диск Фалес Милетский и его теорема
Фалес Милетский и его теорема Теорема Пифагора в картинках
Теорема Пифагора в картинках Степень числа
Степень числа Вычитание дроби из натурального числа
Вычитание дроби из натурального числа Свойства функции. 10 класс
Свойства функции. 10 класс Построение графика функции Y = F(X+L) + M
Построение графика функции Y = F(X+L) + M Действия с натуральными числами. Прикидка и оценка
Действия с натуральными числами. Прикидка и оценка Основные понятия алгебры логики
Основные понятия алгебры логики Признаки параллельности прямых
Признаки параллельности прямых Математическая модель
Математическая модель Стереометрия. Расстояние между скрещивающимися прямыми
Стереометрия. Расстояние между скрещивающимися прямыми Свойства движений. Параллельный перенос
Свойства движений. Параллельный перенос Цифры и числа. Наименьшее и наибольшее натуральное число
Цифры и числа. Наименьшее и наибольшее натуральное число Занятие по математике в средней группе по теме: Геометрические фигуры
Занятие по математике в средней группе по теме: Геометрические фигуры Понятие эксперимента. Классификация видов экспериментальных исследований
Понятие эксперимента. Классификация видов экспериментальных исследований Презентация занятия по ФЭМП с использованием ИКТ в подготовительной группена тему: Путешествие в сказку цветик - семицветик
Презентация занятия по ФЭМП с использованием ИКТ в подготовительной группена тему: Путешествие в сказку цветик - семицветик Решение неравенств второй степени с одной переменной. 9 класс
Решение неравенств второй степени с одной переменной. 9 класс Школа России. 2 класс. Презентация Решение задач
Школа России. 2 класс. Презентация Решение задач Разность квадратов
Разность квадратов