Содержание
- 2. Основы теории логических преобразований Математическая логика Логические операции и элементы Преобразование логических выражений
- 3. 1) Логика оказала влияние на развитие математики, прежде всего теории множеств, функциональных систем, алгоритмов, рекурсивных функций.
- 4. АЛГЕБРА ЛОГИКИ (ВЫСКАЗЫВАНИЙ) - РАЗДЕЛ МАТЕМАТИЧЕСКОЙ ЛОГИКИ, ИЗУЧАЮЩИЙ ВЫСКАЗЫВАНИЯ И ЛОГИЧЕСКИЕ ОПЕРАЦИИ НАД НИМИ.
- 5. Основные понятия Высказывание Простое и сложное высказывание
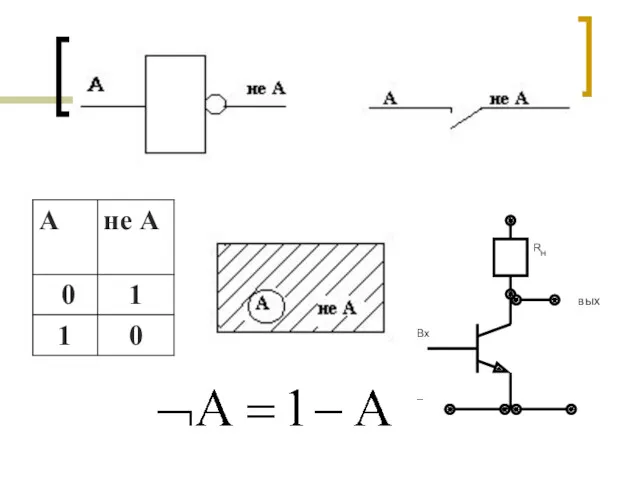
- 6. ИНВЕРСИЯ (ЛОГИЧЕСКОЕ ОТРИЦАНИЕ) - ПРИСОЕДИНЕНИЕ ЧАСТИЦЫ «НЕ» К СКАЗУЕМОМУ ДАННОГО ПРОСТОГО ВЫСКАЗЫВАНИЯ ИЛИ ПРИСОЕДИНЕНИЕ СЛОВ «НЕВЕРНО
- 7. 0 вых
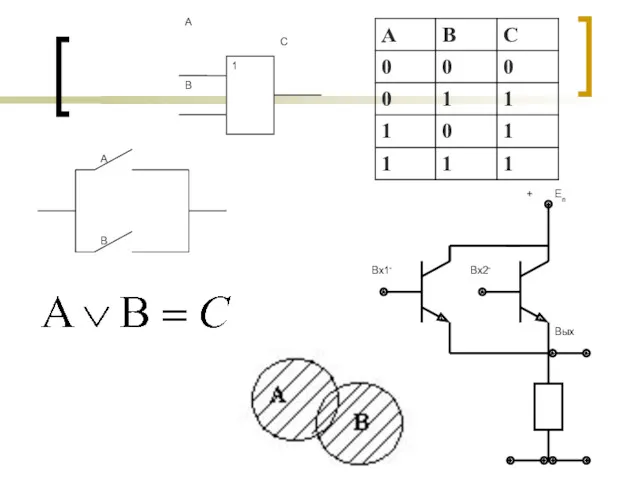
- 8. ДИЗЪЮНКЦИЯ (ЛОГИЧЕСКОЕ СЛОЖЕНИЕ) - СОЕДИНЕНИЕ ДВУХ ВЫСКАЗЫВАНИЙ А И В В ОДНО С ПОМОЩЬЮ СОЮЗА «ИЛИ»,
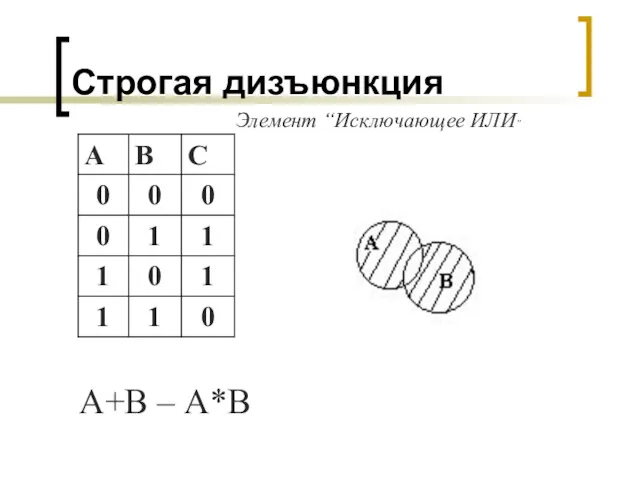
- 10. Строгая дизъюнкция А+В – А*В Элемент “Исключающее ИЛИ”
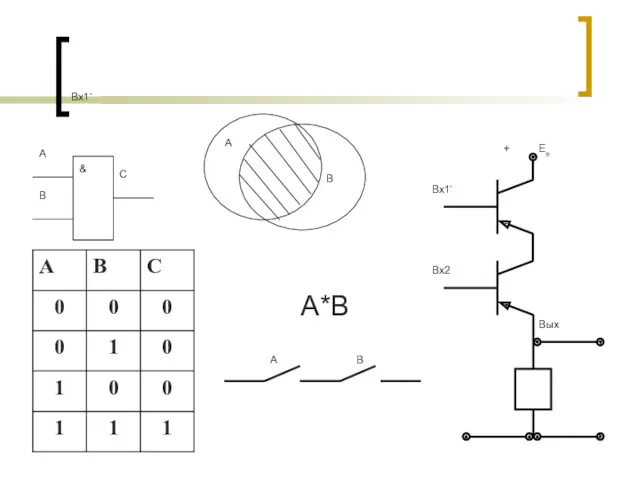
- 11. КОНЪЮНКЦИЯ (ЛОГИЧЕСКОЕ УМНОЖЕНИЕ) - СОЕДИНЕНИЕ ДВУХ ВЫСКАЗЫВАНИЙ А И В В ОДНО С ПОМОЩЬЮ СОЮЗА «И».
- 12. Вх1- А*В
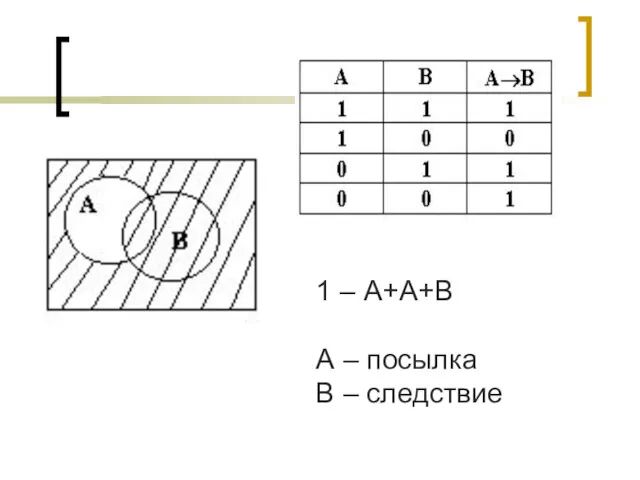
- 13. ИМПЛИКАЦИЯ - ЛОГИЧЕСКАЯ ОПЕРАЦИЯ, СООТВЕТСТВУЮЩАЯ СОЮЗУ «ЕСЛИ . . . , ТО . . .» ИМПЛИКАЦИЯ
- 14. 1 – А+А+В А – посылка В – следствие
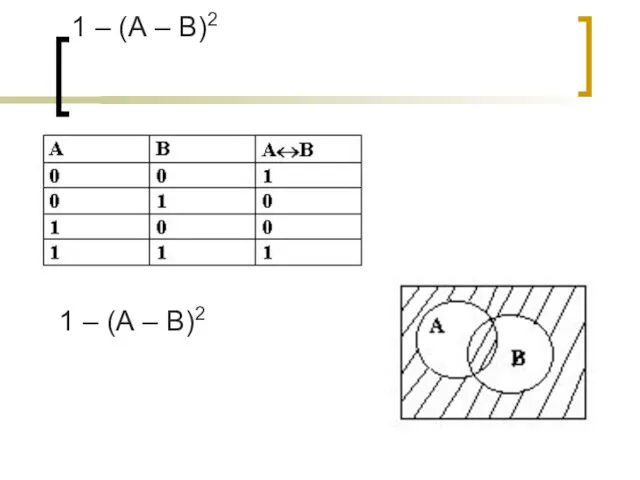
- 15. ЭКВИВАЛЕНЦИЯ - ЛОГИЧЕСКАЯ ОПЕРАЦИЯ, СООТВЕТСТВУЮЩАЯ СОЮЗУ «ТОГДА И ТОЛЬКО ТОГДА, КОГДА …» ЭКВИВАЛЕНЦИЯ ДВУХ ВЫСКАЗЫВАНИЙ ИСТИННА
- 16. 1 – (А – В)2 1 – (А – В)2
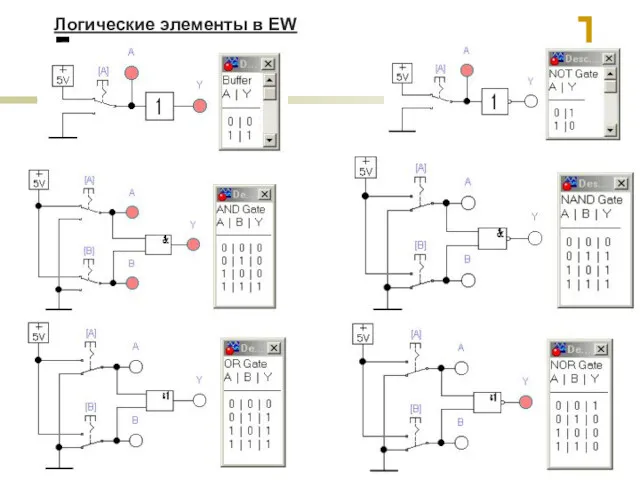
- 17. Логические элементы в EW
- 18. Логические функции Логической (булевой) функцией называют функцию Y=f(Х1, Х2 ..., Хn), аргументы которой Х1, Х2 ...,
- 19. СНДФ и СКНФ Если логическая функция представлена дизъюнкцией, конъюнкцией и инверсией, то такая форма представления называется
- 20. Совершенная дизъюнктивная нормальная форма (СДНФ)отвечает следующим требованиям: 1) в ней нет двух одинаковых элементарных конъюнкций; 2)
- 22. Алгоритм образования СДНФ по таблице истинности. 1. Выделить в таблице истинности все наборы переменных, на которых
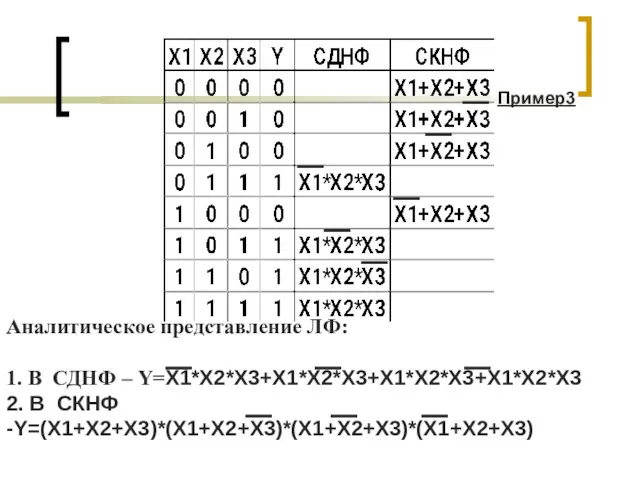
- 24. Аналитическое представление ЛФ: 1. В СДНФ – Y=X1*X2*X3+X1*X2*X3+X1*X2*X3+X1*X2*X3 2. В СКНФ -Y=(X1+X2+X3)*(X1+X2+X3)*(X1+X2+X3)*(X1+X2+X3) Пример3
- 25. Минимизация логических функций Цель минимизации ЛФ заключается уменьшение стоимости ее технической реализации при сохранении заданных характеристик.
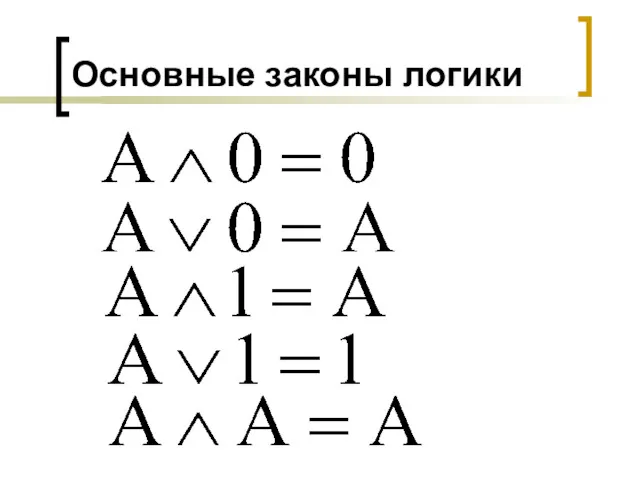
- 26. Основные законы логики
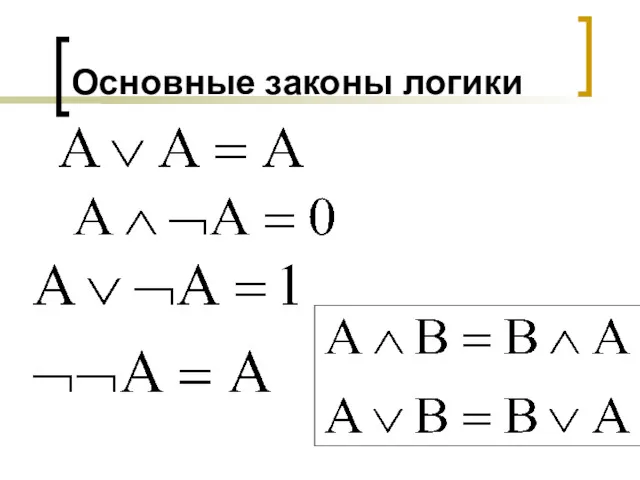
- 27. Основные законы логики
- 30. ВЫСКАЗЫВАНИЕ - ЭТО ПОВЕСТВОВАТЕЛЬНОЕ ПРЕДЛОЖЕНИЕ, О КОТОРОМ МОЖНО СКАЗАТЬ, ЧТО ОНО ИСТИННО ИЛИ ЛОЖНО. 1) Земля
- 31. ВЫСКАЗЫВАНИЕМ НЕ ЯВЛЯЕТСЯ: 1) ВОСКЛИЦАТЕЛЬНЫЕ И ВОПРОСИТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ. 2) ОПРЕДЕЛЕНИЯ. 3) ПРЕДЛОЖЕНИЯ ТИПА: «ОН СЕРОГЛАЗ» «X2-4X+3=0»
- 33. Скачать презентацию



















 Решение задач по теории вероятностей (по материалам открытого банка задач ЕГЭ по математике)
Решение задач по теории вероятностей (по материалам открытого банка задач ЕГЭ по математике) Переместительное свойство умножения
Переместительное свойство умножения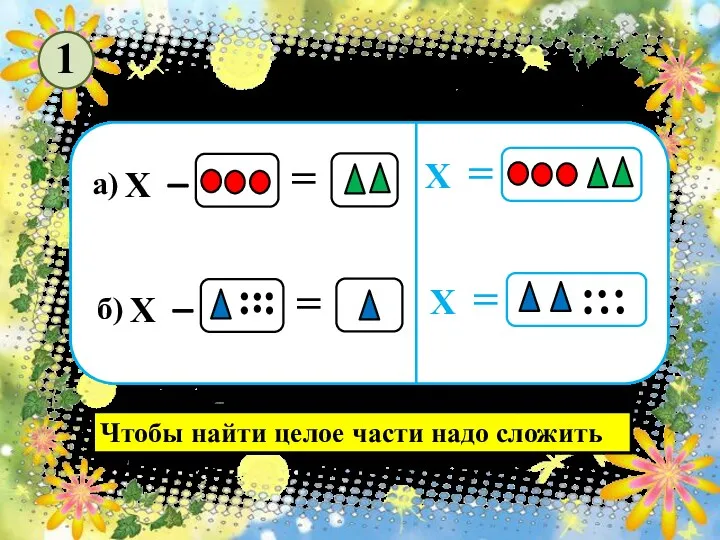 Уравнения. Нахождение уменьшаемого.
Уравнения. Нахождение уменьшаемого. Нахождение неизвестного слагаемого
Нахождение неизвестного слагаемого Решение задач на движение. Средняя скорость
Решение задач на движение. Средняя скорость Число ноль
Число ноль Interval Discrete Equation as a Model of Soil and Groundwater Contamination by Nitrogen
Interval Discrete Equation as a Model of Soil and Groundwater Contamination by Nitrogen Перпендикулярность прямых и плоскостей. Повторение
Перпендикулярность прямых и плоскостей. Повторение Преобразование выражений, содержащих квадратные корни
Преобразование выражений, содержащих квадратные корни Окружность, круг, радиус, диаметр. 5 класс
Окружность, круг, радиус, диаметр. 5 класс Двугранный угол
Двугранный угол Решение уравнений: Нахождение неизвестных делителя и делимого. 6 класс
Решение уравнений: Нахождение неизвестных делителя и делимого. 6 класс С Бибигоном на Луну
С Бибигоном на Луну Лекции по теории функции комплексной переменной
Лекции по теории функции комплексной переменной Касательная. Уравнение касательной
Касательная. Уравнение касательной Повторення вивченого. Запис та складання виразів. Робота над задачами. Геометричний матеріал. Урок №66
Повторення вивченого. Запис та складання виразів. Робота над задачами. Геометричний матеріал. Урок №66 Проверка и оценка знаний таблицы умножения и деления
Проверка и оценка знаний таблицы умножения и деления Поверхности второго порядка
Поверхности второго порядка Подготовка к введению задач в 2 действия. Устный счет
Подготовка к введению задач в 2 действия. Устный счет Упростите выражение
Упростите выражение Углы, связанные с окружностью. Подготовка к ГИА
Углы, связанные с окружностью. Подготовка к ГИА Конспект урока математики в 1 классе
Конспект урока математики в 1 классе Буратино в стране математики
Буратино в стране математики Математика навколо нас
Математика навколо нас Сходимость знакоположительных рядов
Сходимость знакоположительных рядов Карл Фридрих Гаусс
Карл Фридрих Гаусс Длина окружности и площадь круга
Длина окружности и площадь круга Квадратный метр
Квадратный метр