Слайд 2

§15. Сходимость знакоположительных рядов
ЛЕММА 1 (необходимое и достаточное условие сходимости знакоположительного
ряда).
Знакоположительный ряд сходится ⇔ последовательность его частичных сумм ограничена.
ДОКАЗАТЕЛЬСТВО
ТЕОРЕМА 2 (первый признак сравнения).
Пусть ∑un и ∑vn – знакоположительные ряды, причем
un ≤ vn , ∀n≥N (N∈ℕ).
Тогда
1) если ряд ∑vn сходится, то и ряд ∑un тоже сходится;
2) если ряд ∑un расходится, то и ряд ∑vn тоже расходится.
ДОКАЗАТЕЛЬСТВО
Слайд 3

ТЕОРЕМА 3 (второй признак сравнения).
Пусть ∑un и ∑vn – знакоположительные
ряды.
Если при n → ∞ существует конечный и отличный от нуля предел отношения их общих членов, т.е.
то ряды ∑un и ∑vn ведут себя одинаково по отношению к сходимости.
ДОКАЗАТЕЛЬСТВО
Слайд 4

ЭТАЛОННЫЕ РЯДЫ, которые используются в признаках сравнения:
а) гармонический ряд – расходится;
б) обобщенный гармонический
ряд (ряд Дирихле)
в) ряд геометрической прогрессии
Слайд 5

ТЕОРЕМА 4 (признак Даламбера).
Пусть ∑un – знакоположительный ряд и существует
Тогда
а) если ℓ < 1 , то ряд сходится;
б) если ℓ > 1 , то ряд расходится;
в) если ℓ = 1 , то вопрос о сходимости ряда остается открытым.
ДОКАЗАТЕЛЬСТВО
Слайд 6

ТЕОРЕМА 5 (признак Коши).
Пусть ∑un – знакоположительный ряд и существует
Тогда
а) если
ℓ < 1 , то ряд сходится;
б) если ℓ > 1 , то ряд расходится;
в) если ℓ = 1 , то вопрос о сходимости ряда остается открытым.
ДОКАЗАТЕЛЬСТВО
Замечания.
1) В обеих теоремах 4 и 5 случай ℓ = ∞ включается в ℓ > 1 .
2) В ходе доказательства теорем 4 и 5 показывается, что если ℓ > 1 , то





 Развитие алгоритмического мышления младших школьников
Развитие алгоритмического мышления младших школьников Математика – царица всех наук. Математическая викторина
Математика – царица всех наук. Математическая викторина Математические диктанты
Математические диктанты Сравнение многозначных чисел.
Сравнение многозначных чисел.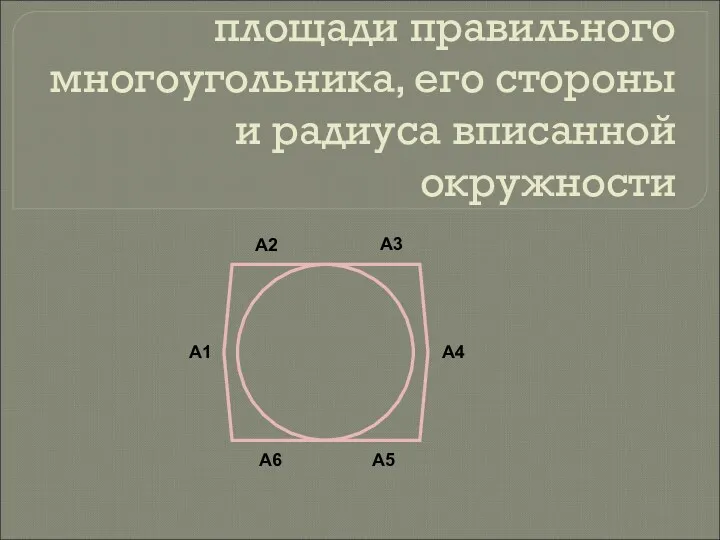 Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности
Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности Игра Математика в мире животных и животные в мире математики
Игра Математика в мире животных и животные в мире математики Решение задач на нахождение дроби от числа
Решение задач на нахождение дроби от числа Решение задач по теме Некоторые свойства касательных, хорд и секущих в окружности
Решение задач по теме Некоторые свойства касательных, хорд и секущих в окружности Математикадан дидактик уеннар
Математикадан дидактик уеннар Число и цифра 4.
Число и цифра 4. Геометрическая прогрессия
Геометрическая прогрессия Решение заданий С1, С3
Решение заданий С1, С3 Выражение с переменной
Выражение с переменной Объем конуса
Объем конуса Быстро называй ответ
Быстро называй ответ Преобразование графиков тригонометрических функций. Интегрированный урок (математика-информатика)
Преобразование графиков тригонометрических функций. Интегрированный урок (математика-информатика) Решение квадратных неравенств
Решение квадратных неравенств Урок математики
Урок математики Пересечение поверхностей
Пересечение поверхностей Ряды Фурье
Ряды Фурье Элементы теории нечетких множеств
Элементы теории нечетких множеств Функции y = tgx и y = ctgx, их свойства и графики
Функции y = tgx и y = ctgx, их свойства и графики Интерактивный тренажёр Состав числа 10
Интерактивный тренажёр Состав числа 10 Прямоугольный треугольник
Прямоугольный треугольник Квадрат и куб (1 класс)
Квадрат и куб (1 класс) Графическое представление данных в виде круговых, столбиковых (столбчатых) диаграмм. 7 класс
Графическое представление данных в виде круговых, столбиковых (столбчатых) диаграмм. 7 класс Додавання і множення числових нерівностей. 9 клас
Додавання і множення числових нерівностей. 9 клас Логарифмическая функция, её свойства и график
Логарифмическая функция, её свойства и график