Содержание
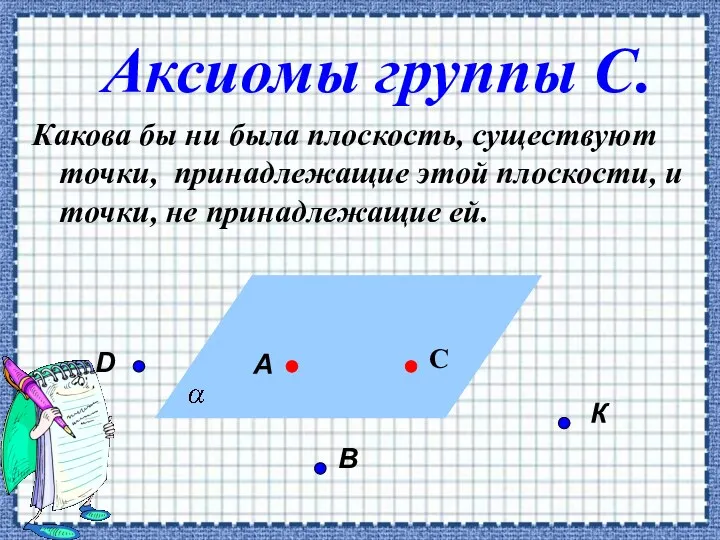
- 2. Аксиомы группы С. Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не
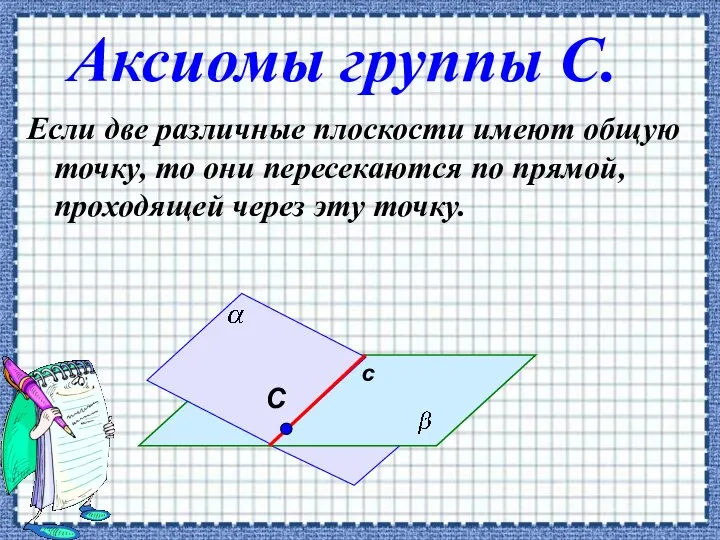
- 3. Аксиомы группы С. Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей
- 4. Аксиомы группы С. Если две различные прямые имеют общую точку, то через них можно провести плоскость,
- 5. Через любую прямую и не принадлежащую ей точку можно провести плоскость, и притом только одну. α
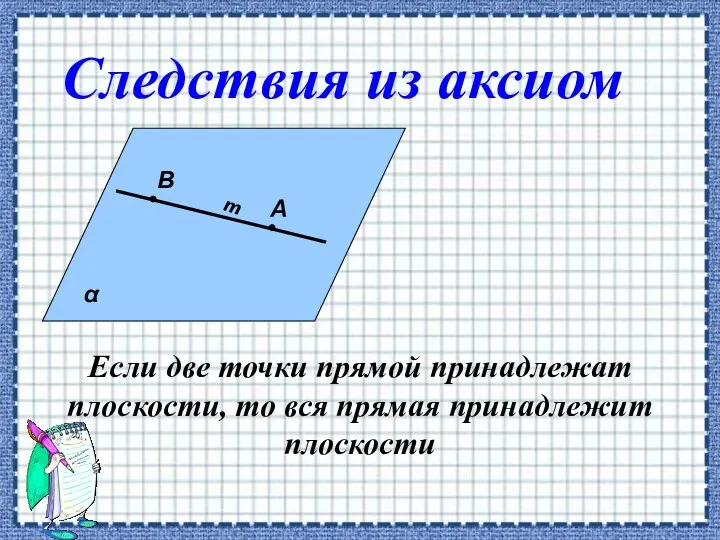
- 6. Если две точки прямой принадлежат плоскости, то вся прямая принадлежит плоскости α А В Следствия из
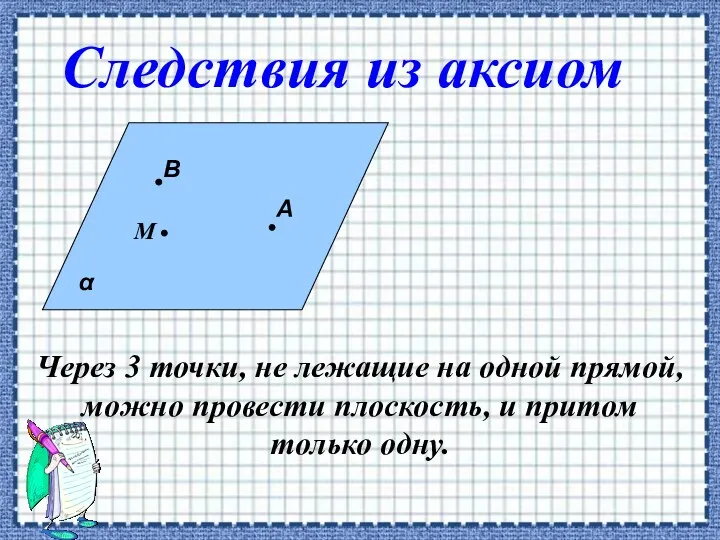
- 7. Через 3 точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну. α
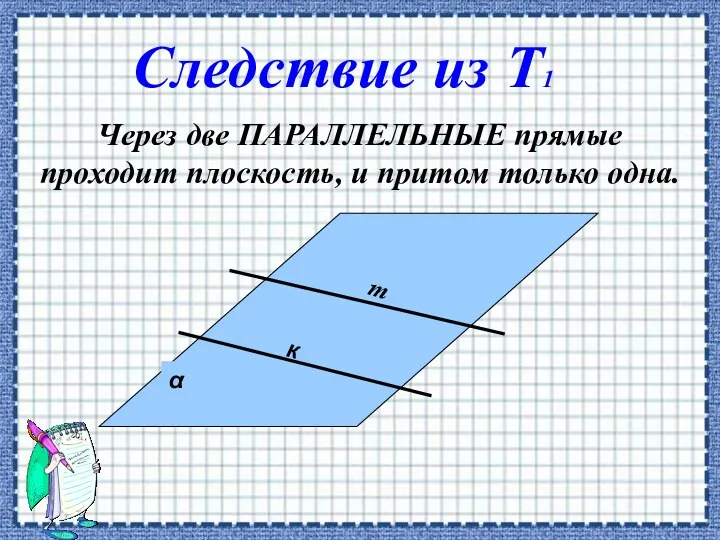
- 8. Через две ПАРАЛЛЕЛЬНЫЕ прямые проходит плоскость, и притом только одна. к Следствие из Т1
- 9. Вывод Как в пространстве можно однозначно задать плоскость? 1. По трем точкам 2. По прямой и
- 10. Определите: верно, ли утверждение?
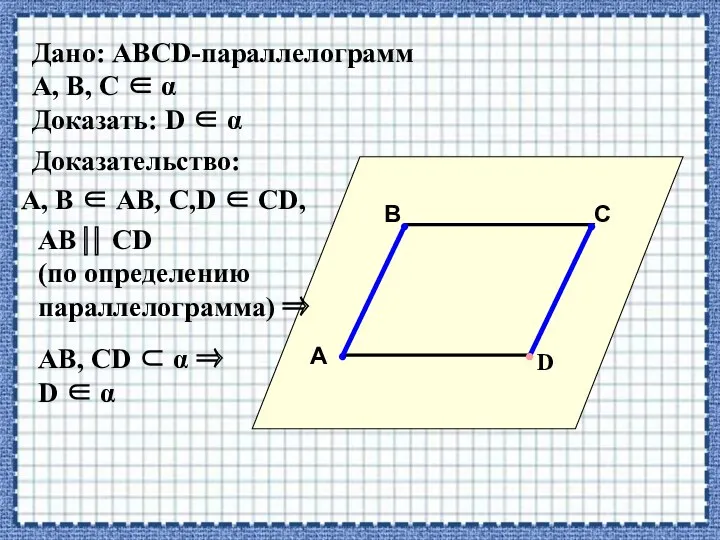
- 11. Дано: АВСD-параллелограмм А, В, С ∈ α Доказать: D ∈ α А В С D •
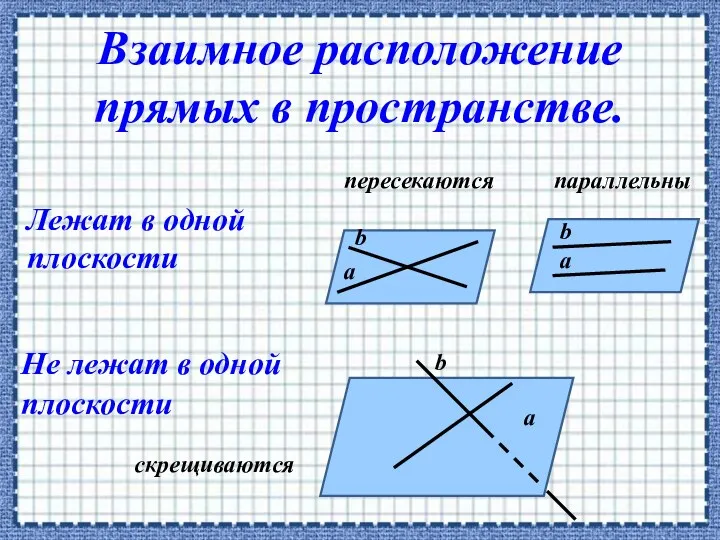
- 12. пересекаются параллельны а а а b b b скрещиваются Лежат в одной плоскости Не лежат в
- 13. Доказательство: а с в1 в β α γ В 1 случай. а, в, с ∈α рассмотрен
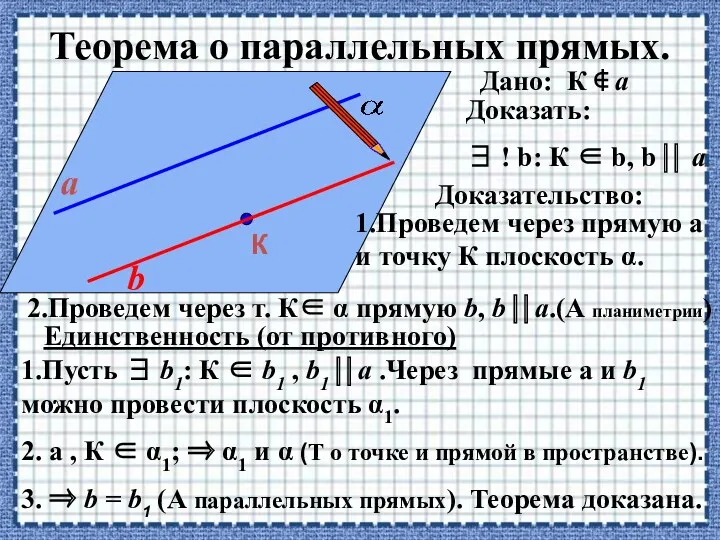
- 14. Теорема о параллельных прямых. К a b Дано: К ∉ a Доказать: ∃ ! b: К
- 15. Задание 1 Вставьте пропущенные слова Единственную плоскость можно задать через три точки, при этом они …………
- 16. Задание 2 Определите: верно, ли утверждение?
- 17. Задание 2 Определите: верно, ли утверждение?
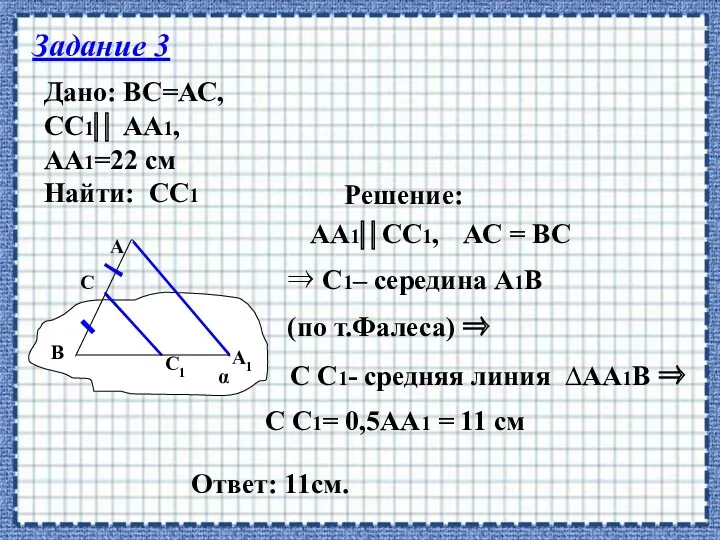
- 18. Задание 3 Дано: ВС=АС, СС1⎜⎜ АА1, АА1=22 см Найти: СС1 Решение: АА1⎜⎜СС1, АС = ВС ⇒
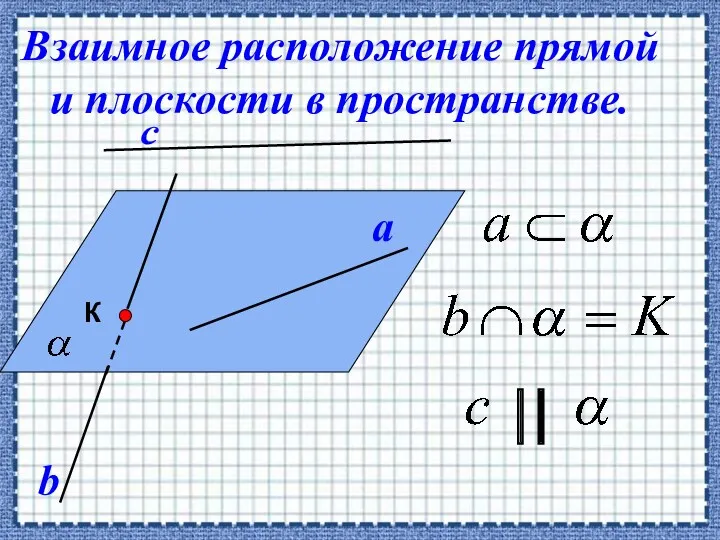
- 19. Взаимное расположение прямой и плоскости в пространстве.
- 20. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости , то
- 21. 1.Через прямые a и b проведем плоскость α Пусть , , α 2. α ∩ β
- 22. Дано: а ⎜⎜ α а ⊂ β; β ∩ α = в Доказать: а ⎜⎜ в
- 24. Скачать презентацию











 Интегральное исчисление функций одной переменной
Интегральное исчисление функций одной переменной Задачи из пособия Р. К. Гордина
Задачи из пособия Р. К. Гордина Конспект урока и презентация по теме Длина ломаной
Конспект урока и презентация по теме Длина ломаной Вычитание двузначных чисел.
Вычитание двузначных чисел. Умножение и деление десятичных дробей
Умножение и деление десятичных дробей Сравнение десятичных дробей для урока
Сравнение десятичных дробей для урока Математика на службе у экологии
Математика на службе у экологии Ряды динамики
Ряды динамики Внеклассное мероприятие по математике для 5-6 классов Своя игра
Внеклассное мероприятие по математике для 5-6 классов Своя игра Задачи на чертежах по теме трапеция
Задачи на чертежах по теме трапеция Дециметр (1 класс)
Дециметр (1 класс) Игра Математика в мире животных и животные в мире математики
Игра Математика в мире животных и животные в мире математики Математика 4 класс
Математика 4 класс Показательные уравнения
Показательные уравнения Состав чисел первого десятка. Тренажёр Мотыльки. 1 класс
Состав чисел первого десятка. Тренажёр Мотыльки. 1 класс Исследовательский проект Многогранники и кристаллы
Исследовательский проект Многогранники и кристаллы Перпендикуляр и наклонная
Перпендикуляр и наклонная Решение задач с помощью частей
Решение задач с помощью частей Аксиомы стереометрии и их простейшие следствия
Аксиомы стереометрии и их простейшие следствия Упражнения для устного счёта по математике в 5 классе
Упражнения для устного счёта по математике в 5 классе Умножение положительных и отрицательных чисел. 6 класс
Умножение положительных и отрицательных чисел. 6 класс Фрагмент презентации к уроку математики в 4 классе
Фрагмент презентации к уроку математики в 4 классе Порядок выполнения действий
Порядок выполнения действий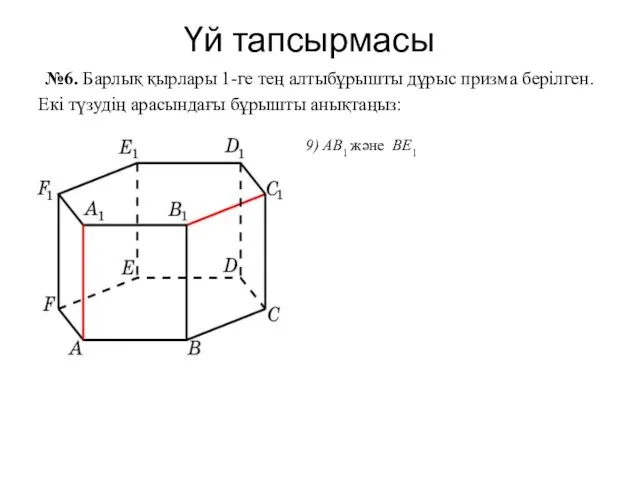 Түзу мен жазықтық арасындағы бұрыш
Түзу мен жазықтық арасындағы бұрыш Взаимное расположение плоскостей, прямой и плоскости на чертежах
Взаимное расположение плоскостей, прямой и плоскости на чертежах Квадратные уравнения. Виды и способы решения
Квадратные уравнения. Виды и способы решения Решение задач обязательной части ОГЭ по геометрии
Решение задач обязательной части ОГЭ по геометрии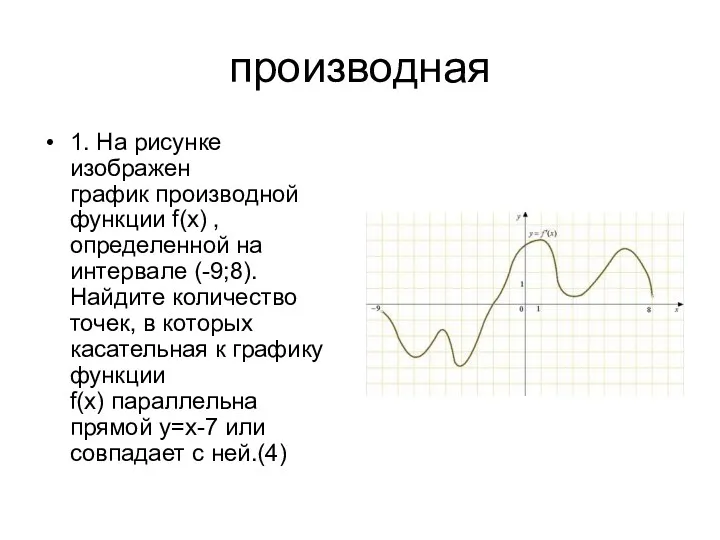 Производная. График производной функции
Производная. График производной функции