Содержание
- 2. План 1. Предмет и задачи теории графов. 2. Понятие графа. 3. Способы описания графов.
- 3. ВВЕДЕНИЕ На практике часто бывает полезно изобразить структуру системы в виде рисунков, составленных из точек (вершин)
- 4. ВВЕДЕНИЕ Граф-модели применяются для эффективного использования ресурсов вычислительной системы (оптимизация использования памяти, уменьшение обменов между оперативной
- 5. План 1. Предмет и задачи теории графов. 2. Понятие графа. 3. Способы описания графов.
- 6. ПРЕДМЕТ И ЗАДАЧИ ТЕОРИИ ГРАФОВ Определения. Основные понятия. Способы задания графов Основные типы графов Операции над
- 7. ПОНЯТИЕ ГРАФА Основной объект теории графов — граф и его обобщения
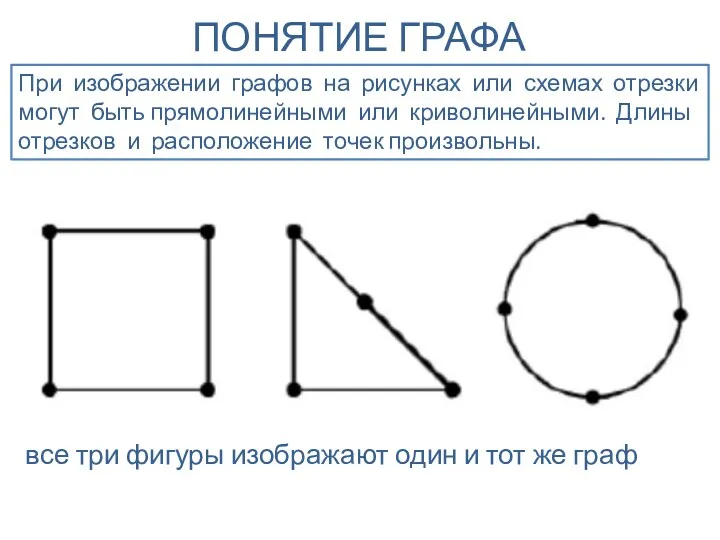
- 8. ПОНЯТИЕ ГРАФА При изображении графов на рисунках или схемах отрезки могут быть прямолинейными или криволинейными. Длины
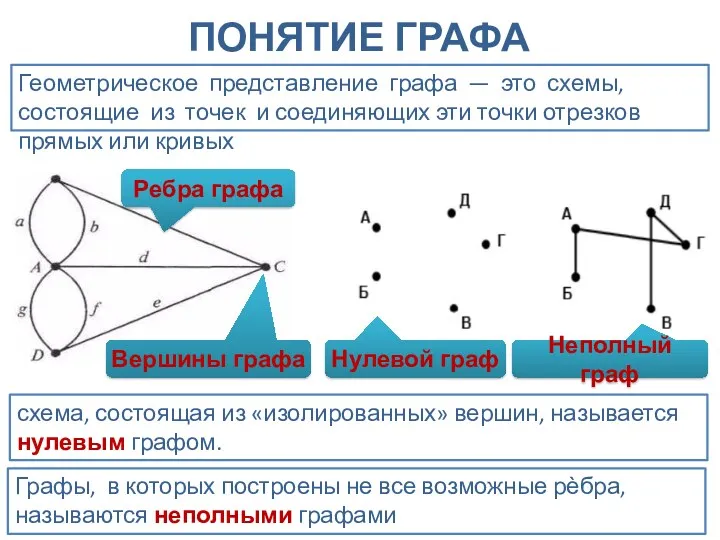
- 9. ПОНЯТИЕ ГРАФА Геометрическое представление графа — это схемы, состоящие из точек и соединяющих эти точки отрезков
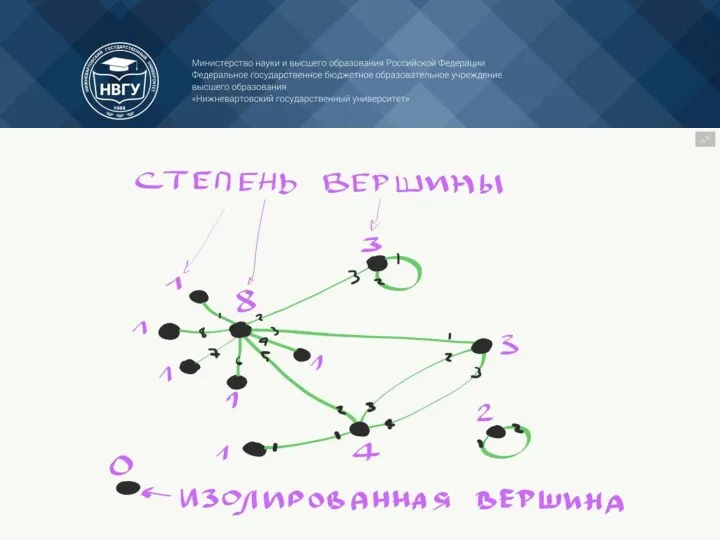
- 10. Вершина - точка в графе, отдельный объект, для топологической модели графа не имеет значения координата вершины,
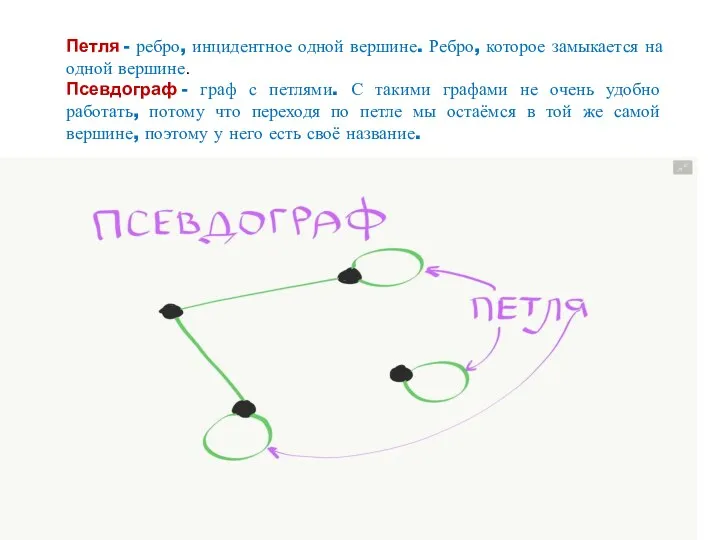
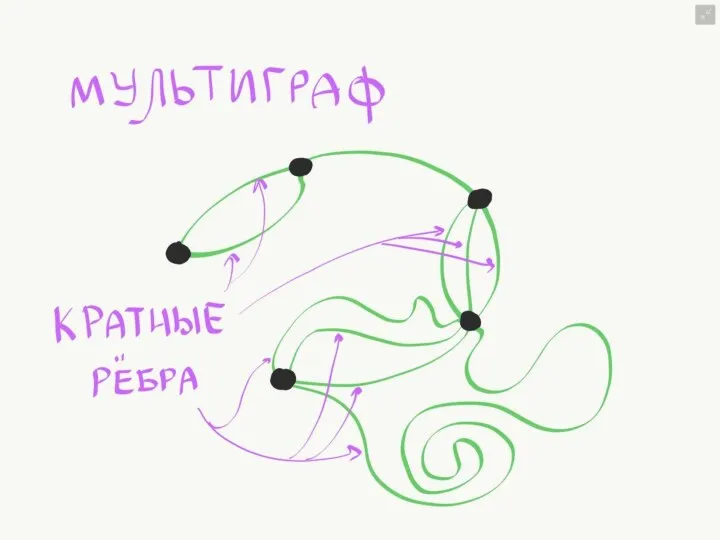
- 13. Петля - ребро, инцидентное одной вершине. Ребро, которое замыкается на одной вершине. Псевдограф - граф с
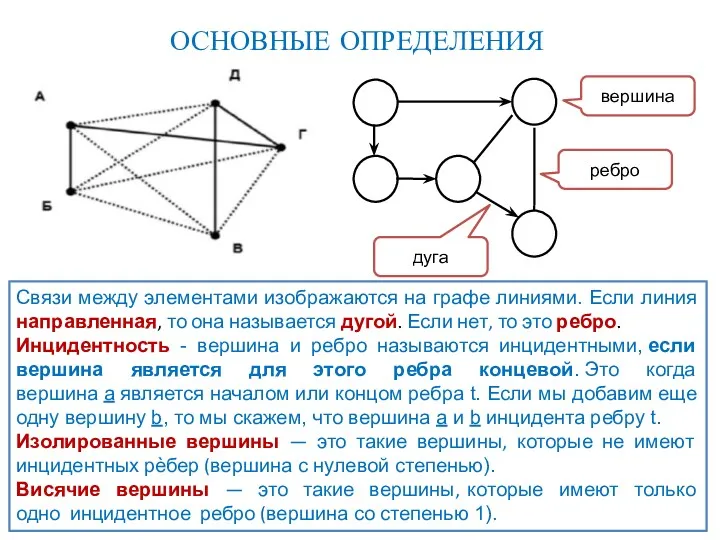
- 14. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ Связи между элементами изображаются на графе линиями. Если линия направленная, то она называется дугой.
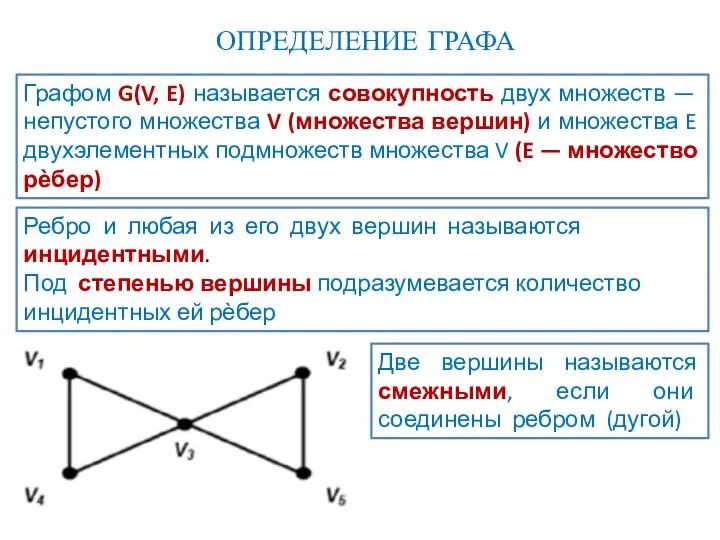
- 16. ОПРЕДЕЛЕНИЕ ГРАФА Ребро и любая из его двух вершин называются инцидентными. Под степенью вершины подразумевается количество
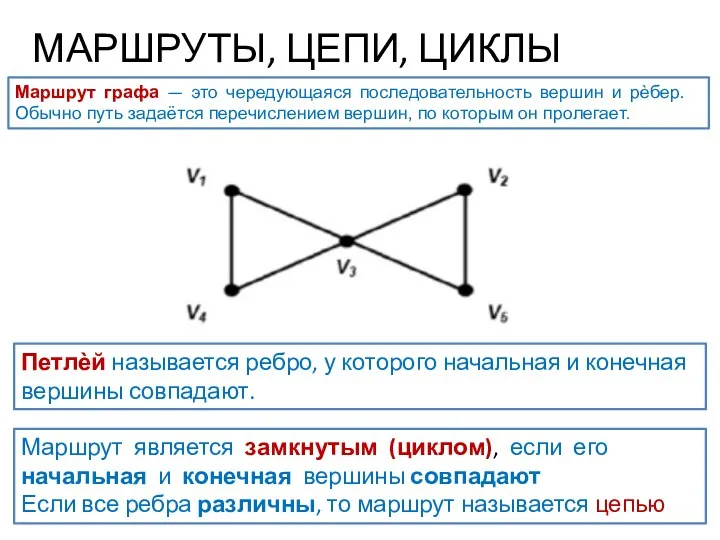
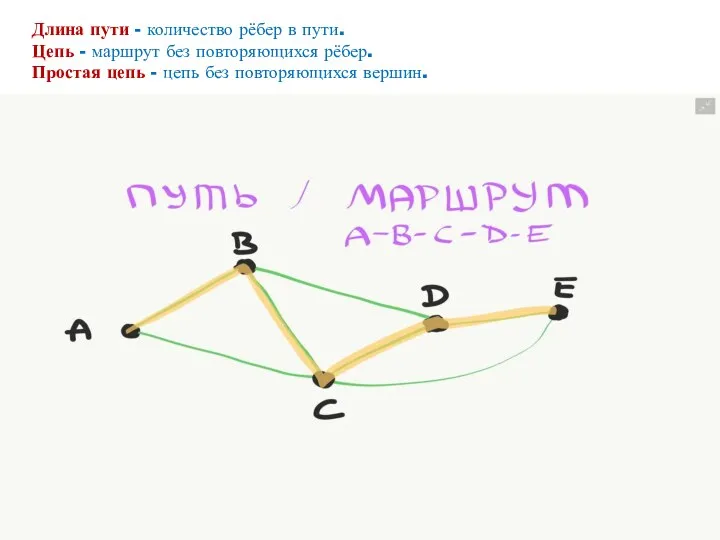
- 17. МАРШРУТЫ, ЦЕПИ, ЦИКЛЫ Маршрут графа — это чередующаяся последовательность вершин и рѐбер. Обычно путь задаётся перечислением
- 18. Длина пути - количество рёбер в пути. Цепь - маршрут без повторяющихся рёбер. Простая цепь -
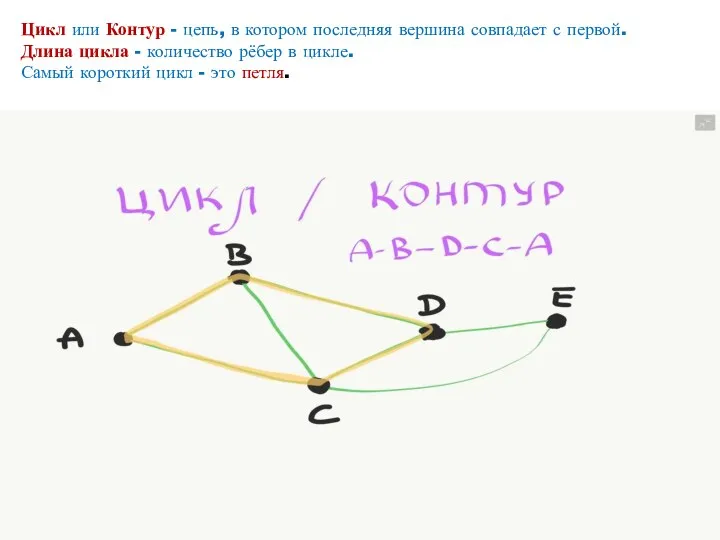
- 19. Цикл или Контур - цепь, в котором последняя вершина совпадает с первой. Длина цикла - количество
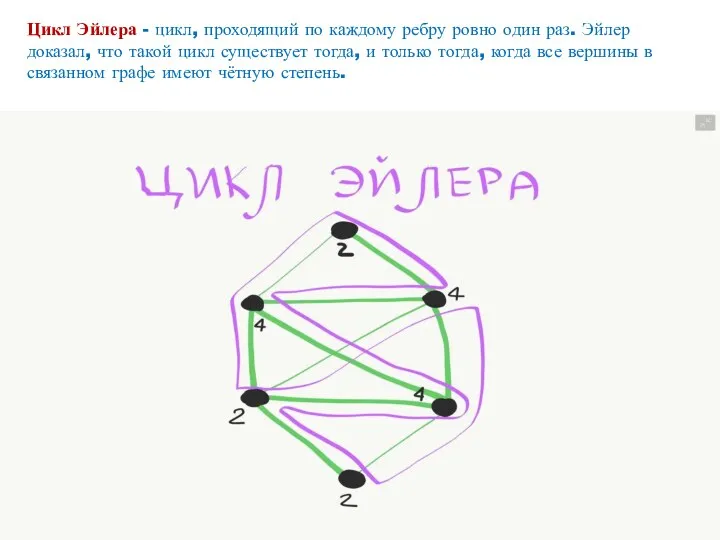
- 20. Цикл Эйлера - цикл, проходящий по каждому ребру ровно один раз. Эйлер доказал, что такой цикл
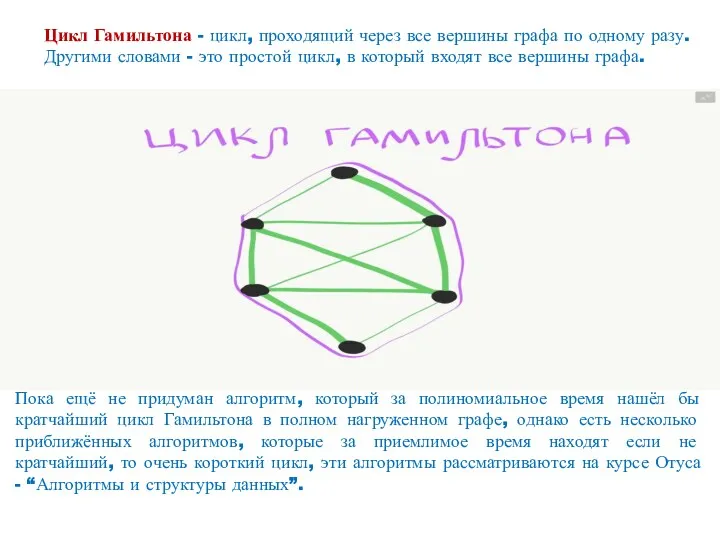
- 21. Цикл Гамильтона - цикл, проходящий через все вершины графа по одному разу. Другими словами - это
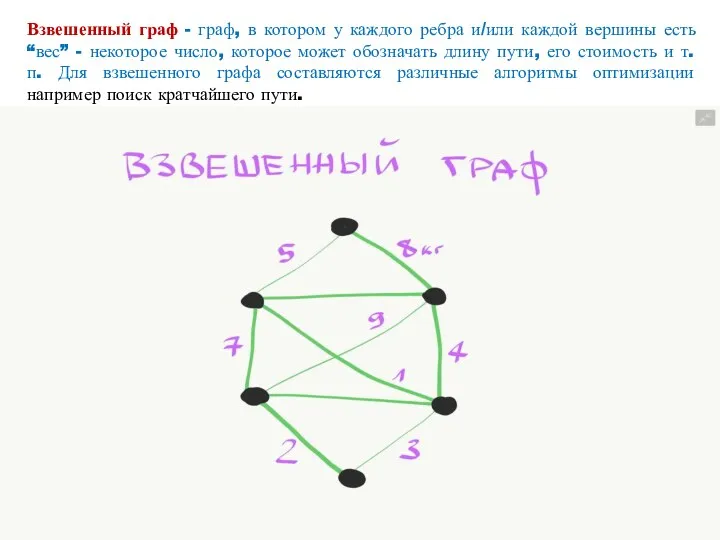
- 22. Взвешенный граф - граф, в котором у каждого ребра и/или каждой вершины есть “вес” - некоторое
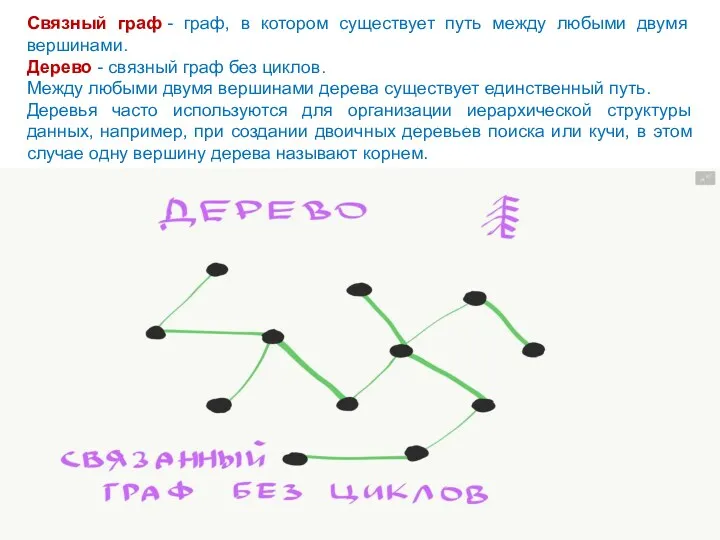
- 23. Связный граф - граф, в котором существует путь между любыми двумя вершинами. Дерево - связный граф
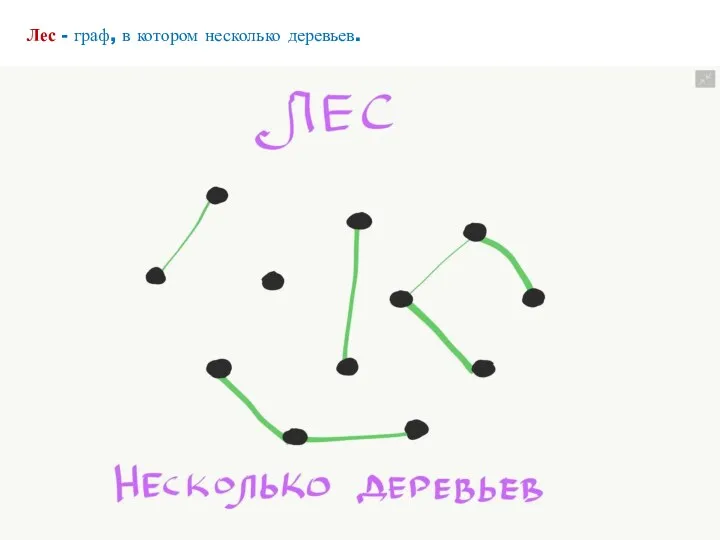
- 24. Лес - граф, в котором несколько деревьев.
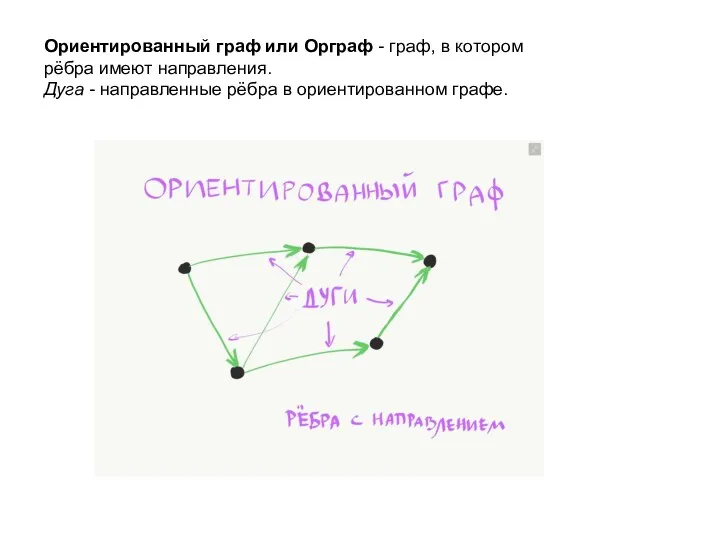
- 25. Ориентированный граф или Орграф - граф, в котором рёбра имеют направления. Дуга - направленные рёбра в
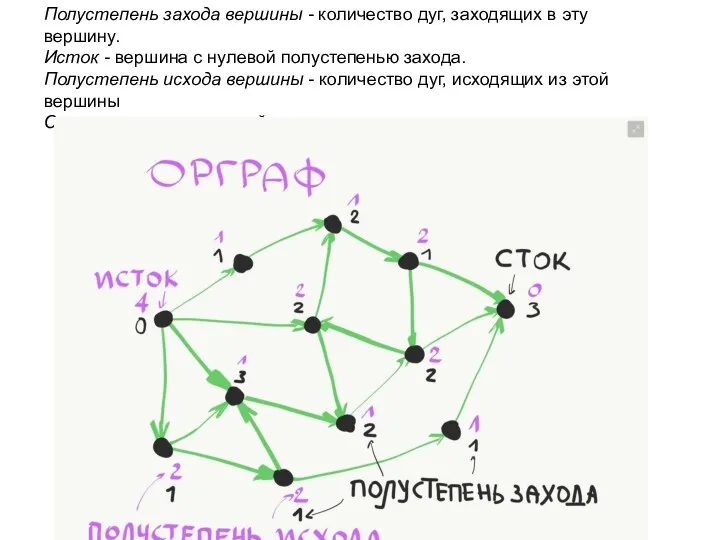
- 26. Полустепень захода вершины - количество дуг, заходящих в эту вершину. Исток - вершина с нулевой полустепенью
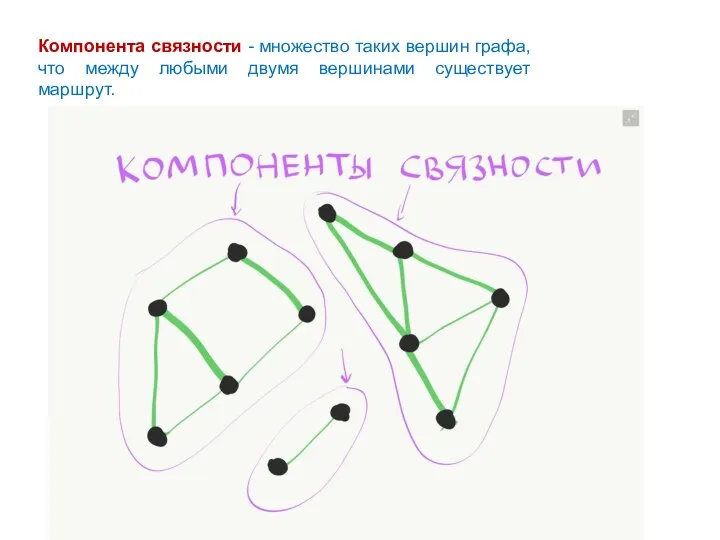
- 27. Компонента связности - множество таких вершин графа, что между любыми двумя вершинами существует маршрут.
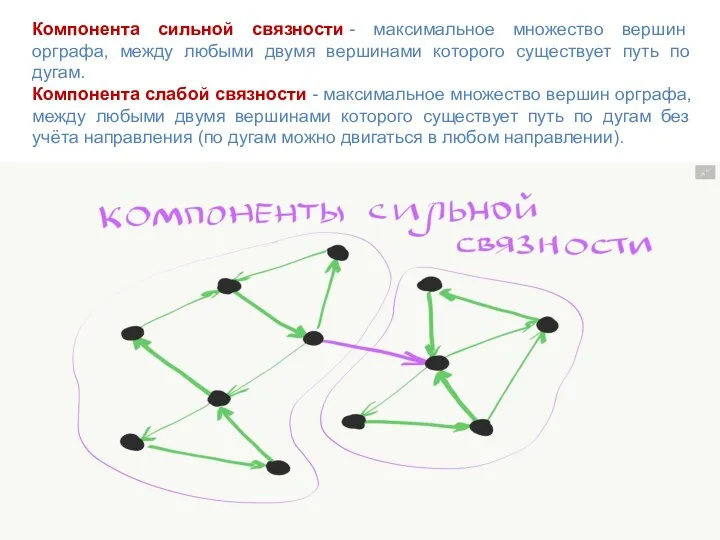
- 28. Компонента сильной связности - максимальное множество вершин орграфа, между любыми двумя вершинами которого существует путь по
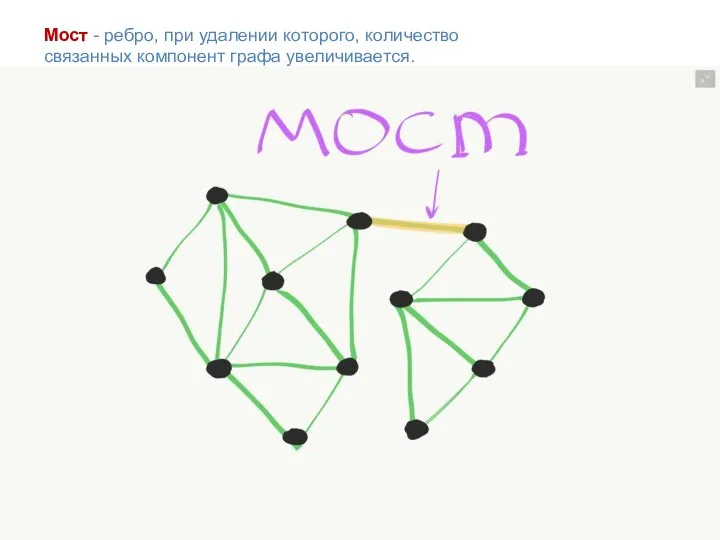
- 29. Мост - ребро, при удалении которого, количество связанных компонент графа увеличивается.
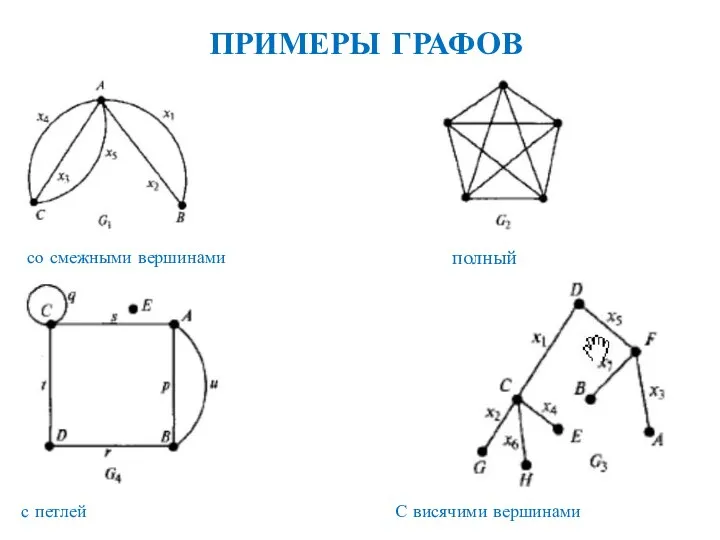
- 30. ПРИМЕРЫ ГРАФОВ со смежными вершинами полный с петлей С висячими вершинами
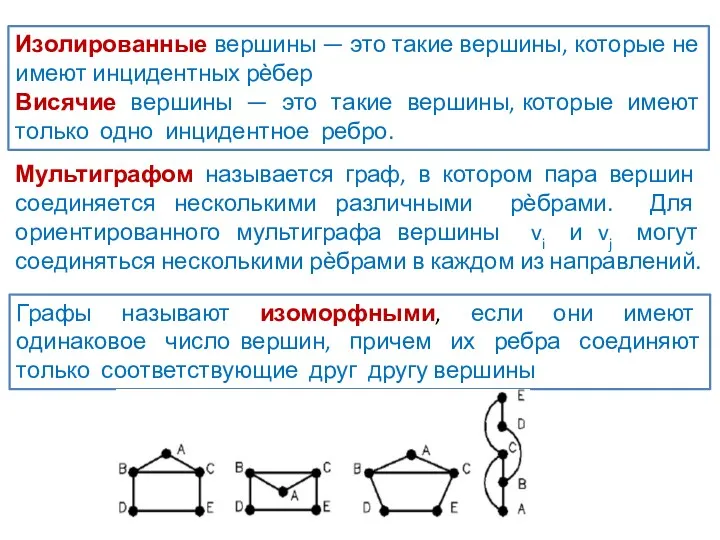
- 31. Изолированные вершины — это такие вершины, которые не имеют инцидентных рѐбер Висячие вершины — это такие
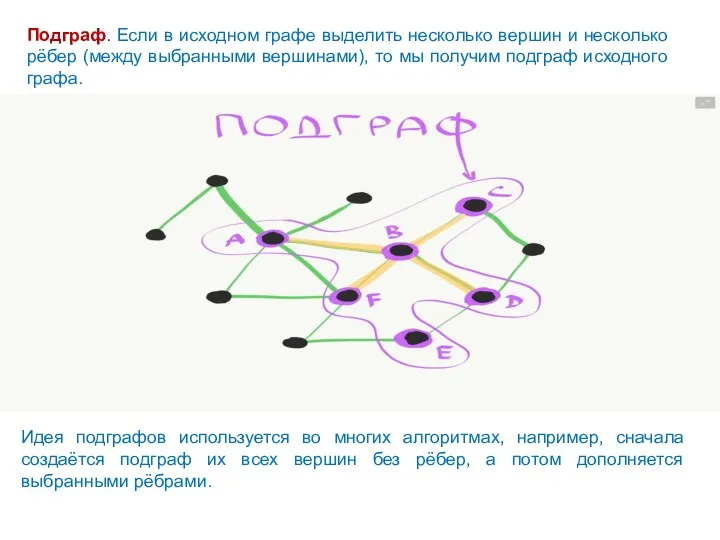
- 33. Подграф. Если в исходном графе выделить несколько вершин и несколько рёбер (между выбранными вершинами), то мы
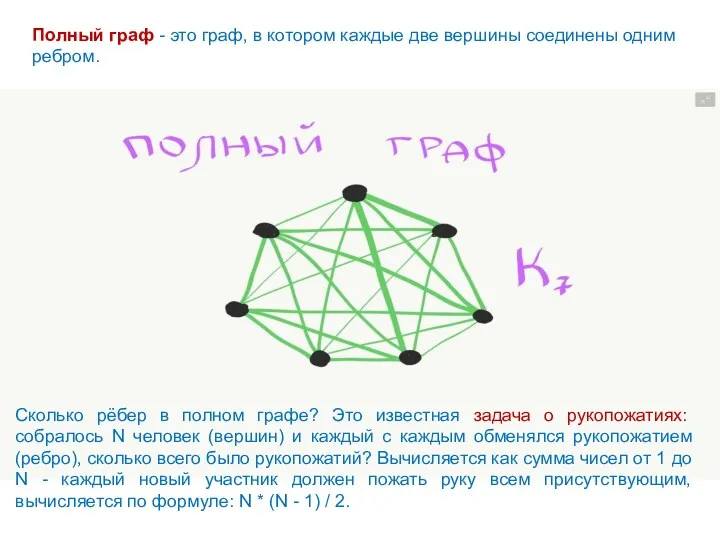
- 34. Полный граф - это граф, в котором каждые две вершины соединены одним ребром. Сколько рёбер в
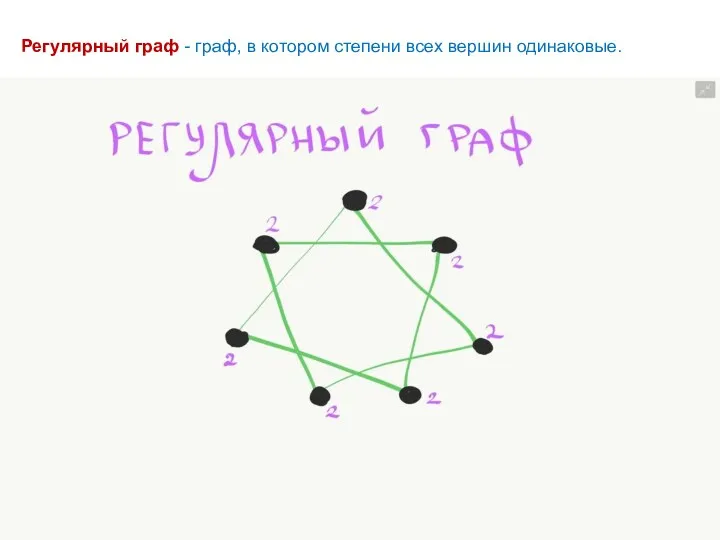
- 35. Регулярный граф - граф, в котором степени всех вершин одинаковые.
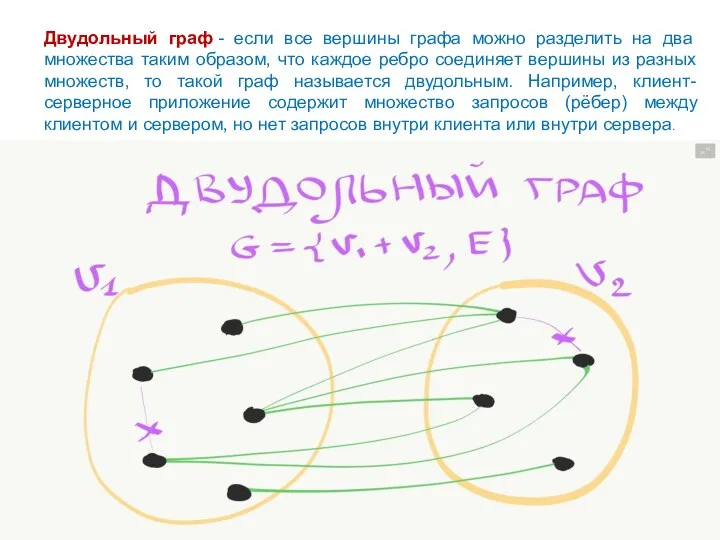
- 36. Двудольный граф - если все вершины графа можно разделить на два множества таким образом, что каждое
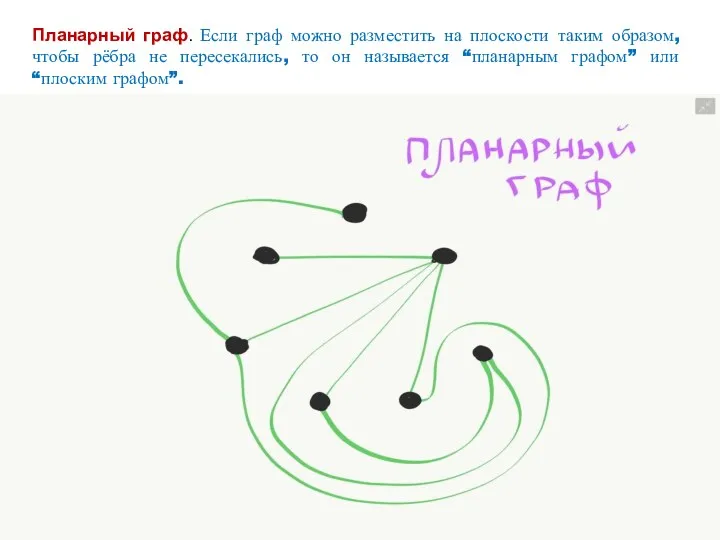
- 37. Планарный граф. Если граф можно разместить на плоскости таким образом, чтобы рёбра не пересекались, то он
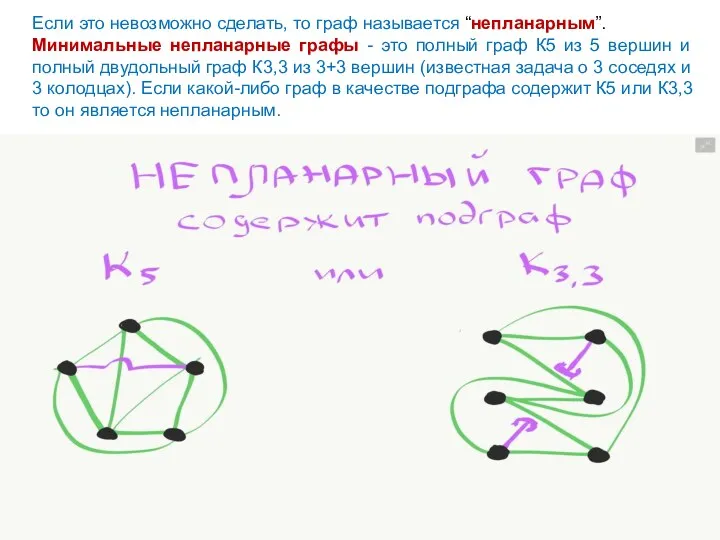
- 38. Если это невозможно сделать, то граф называется “непланарным”. Минимальные непланарные графы - это полный граф К5
- 39. СПОСОБЫ ЗАДАНИЯ ГРАФОВ Перечисление элементов Изображение Матрица смежности Матрица инциденций Списки смежности чтобы задать граф, достаточно
- 40. СПОСОБЫ ОПИСАНИЯ ГРАФОВ Перечисление элементов Изображение Матрица смежности Матрица инциденций Списки смежности Матрица смежности – это
- 41. Матрица смежности Смежность – понятие, используемое только в отношении двух ребер или в отношении двух вершин:
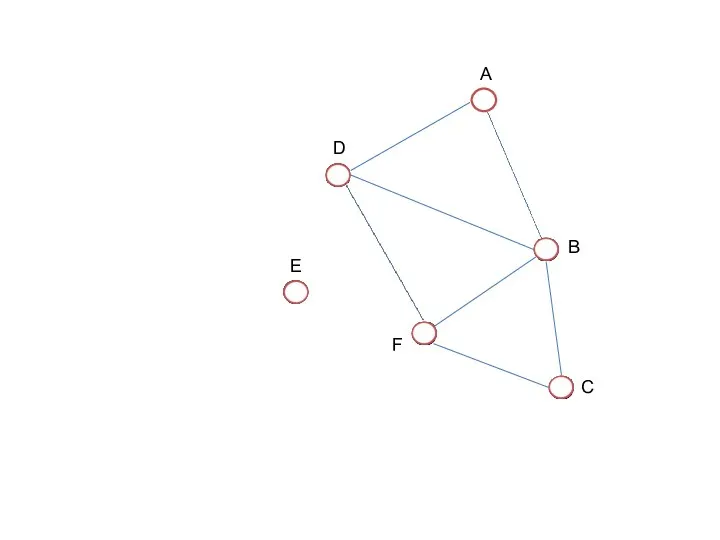
- 42. Для практического примера рассмотрим самый обыкновенный неориентированный граф:
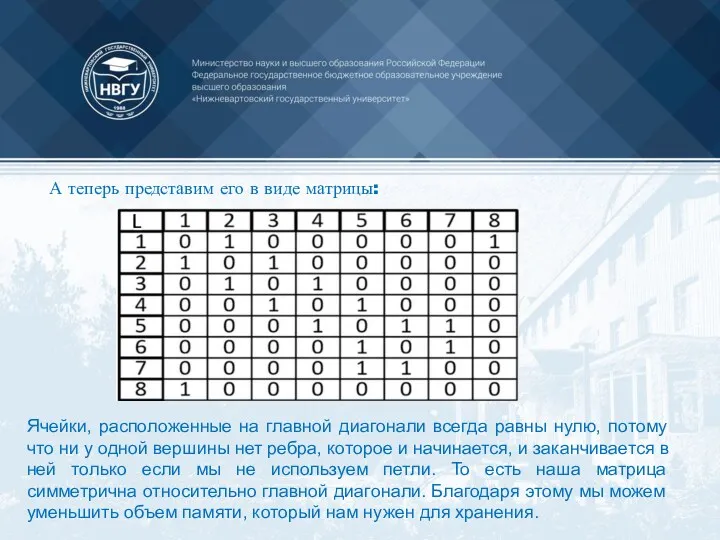
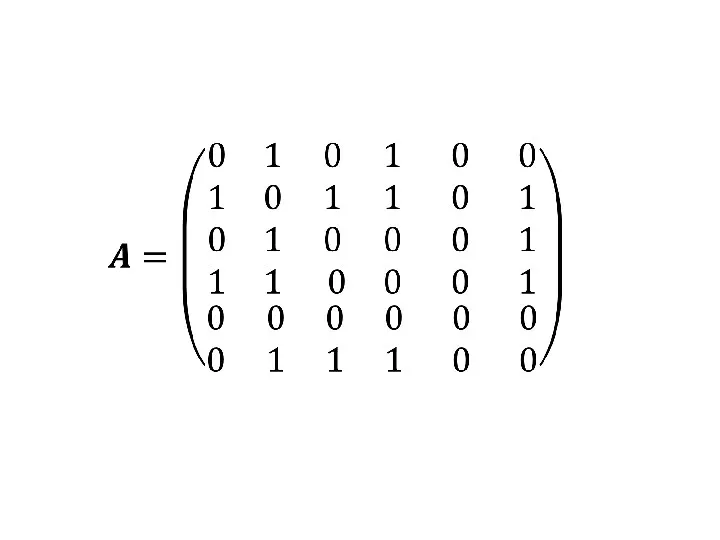
- 43. А теперь представим его в виде матрицы: Ячейки, расположенные на главной диагонали всегда равны нулю, потому
- 44. Если граф неориентированный, то, когда мы просуммируем строку или столбец мы узнаем степень рассматриваемой нами вершины.
- 46. Если мы работаем со строкой матрицы, то мы имеем элемент из которого выходит ребро, в нашем
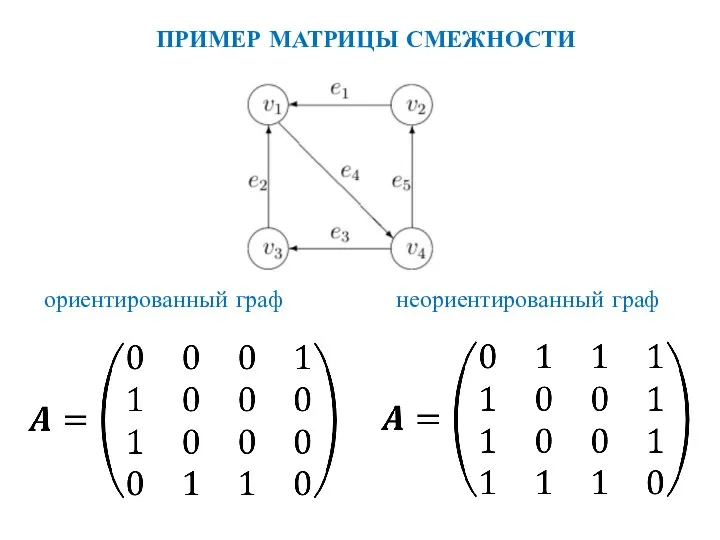
- 47. ПРИМЕР МАТРИЦЫ СМЕЖНОСТИ ориентированный граф неориентированный граф
- 48. СПОСОБЫ ОПИСАНИЯ ГРАФОВ Перечисление элементов Изображение Матрица смежности Матрица инцидентности Списки смежности
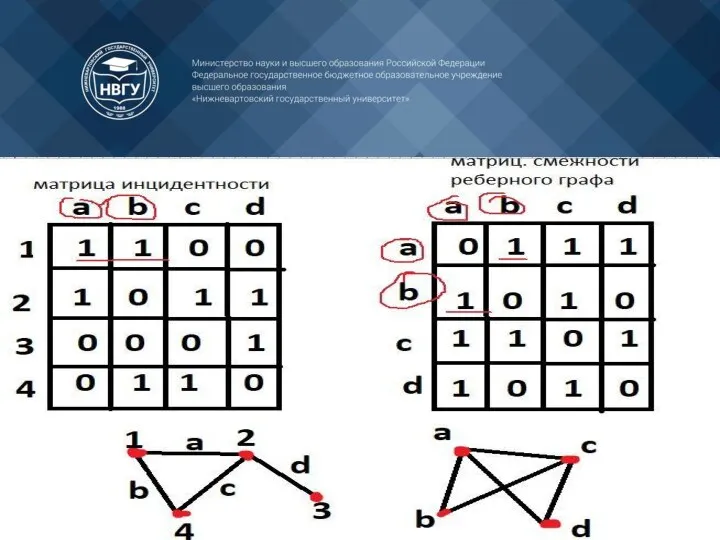
- 49. Матрица инцидентности Инцидентность – понятие, используемое только в отношении ребра и вершины: две вершины (или два
- 50. Сразу же иллюстрируем данное правило:
- 51. Сумма элементов i-ой строки равна степени вершины. При ориентированным графе, ячейка I (i, j) равна 1,
- 52. Ориентированный граф: В виде матрицы:
- 53. Одной из особенностей данной матрицы является то, что в столбце может быть только две ненулевых ячейки.
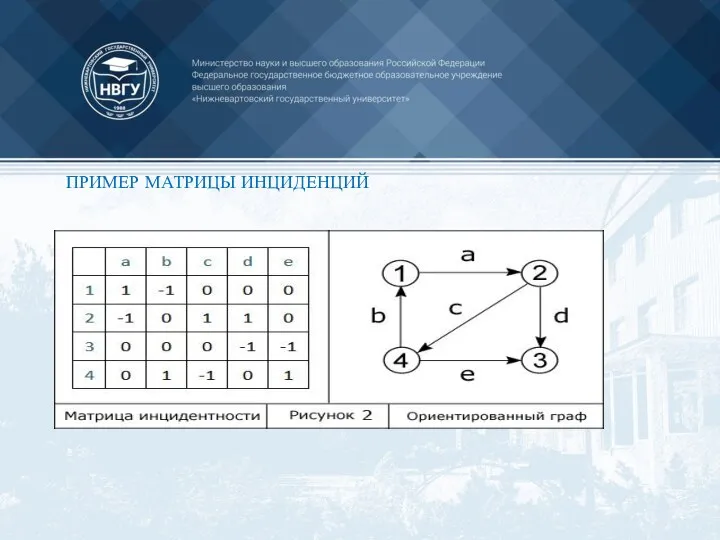
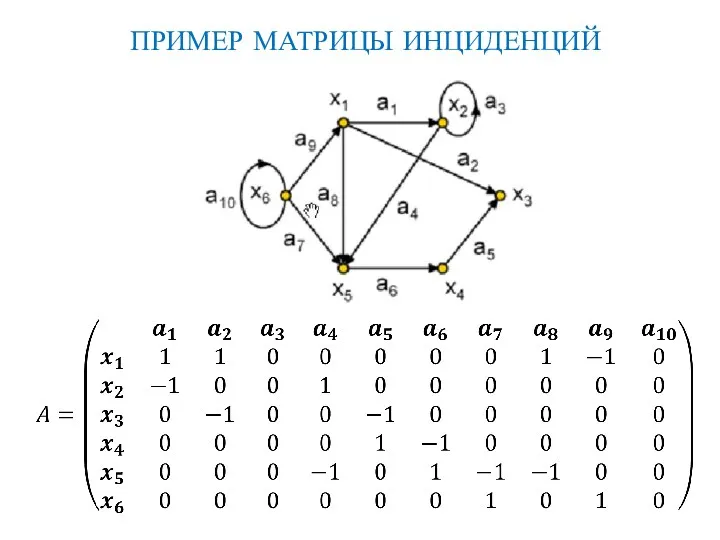
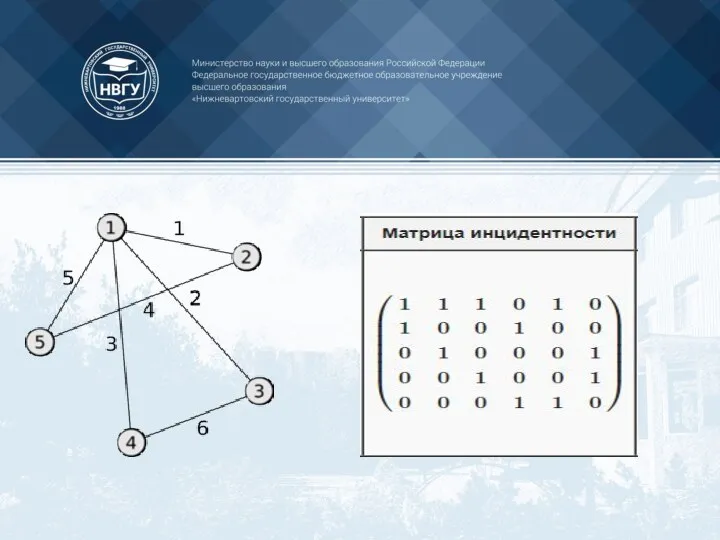
- 54. ПРИМЕР МАТРИЦЫ ИНЦИДЕНЦИЙ
- 56. ПРИМЕР МАТРИЦЫ ИНЦИДЕНЦИЙ
- 59. СПОСОБЫ ОПИСАНИЯ ГРАФОВ Перечисление элементов Изображение Матрица смежности Матрица инцидентности Списки смежности Этот способ часто используется
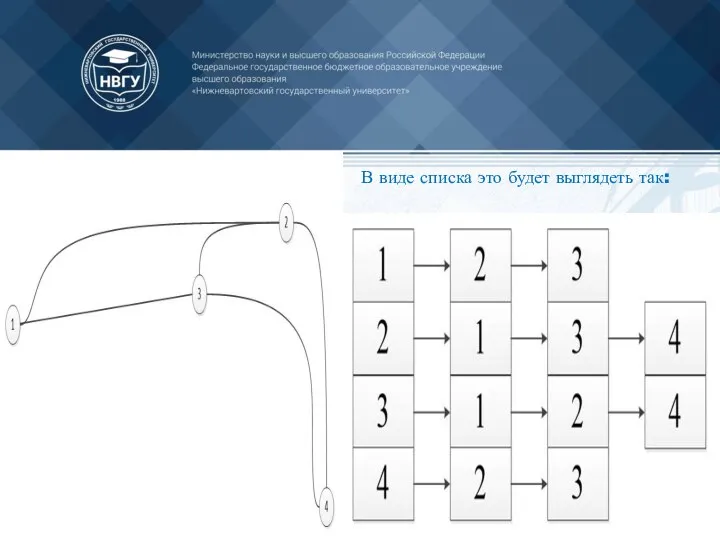
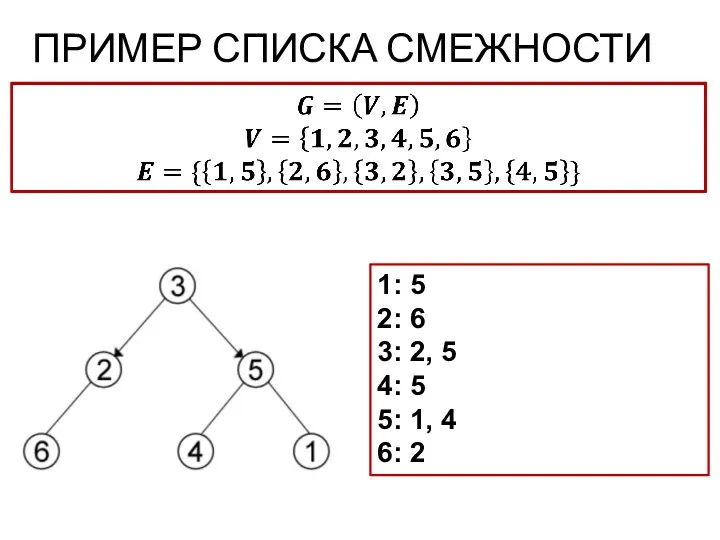
- 60. Список смежности (инцидентности) Список смежности подразумевает под собой, то что мы работаем с некоторым списком (массивом).
- 61. В виде списка это будет выглядеть так:
- 62. Неважно в каком порядке вы расположите ссылку так как вы рассматриваете смежность относительно первой ячейки, все
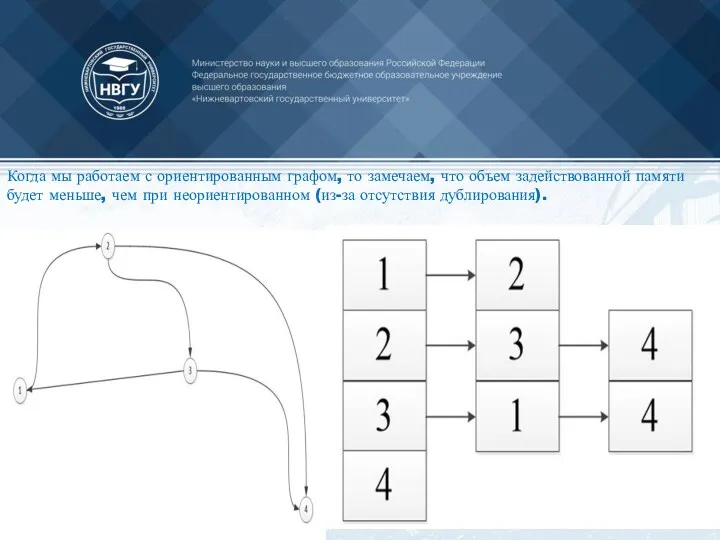
- 63. Когда мы работаем с ориентированным графом, то замечаем, что объем задействованной памяти будет меньше, чем при
- 64. ПРИМЕР СПИСКА СМЕЖНОСТИ 1: 5 2: 6 3: 2, 5 4: 5 5: 1, 4 6:
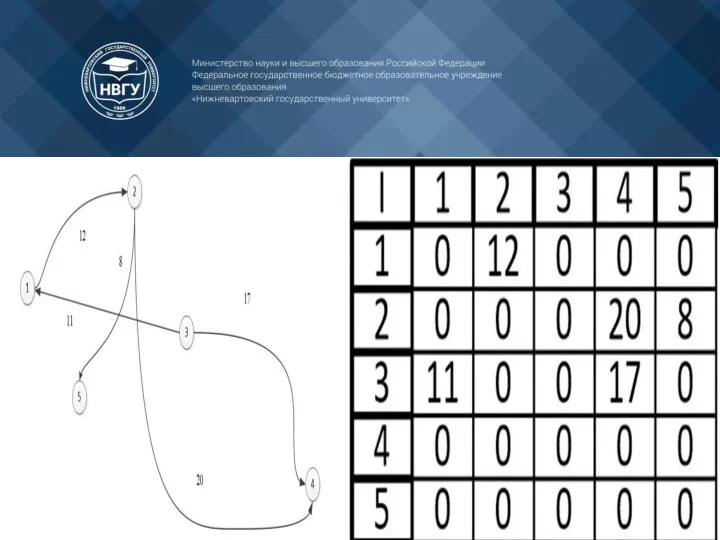
- 65. Взвешенность графа Взвешенный граф - это граф, в котором вместо 1 обозначающее наличие связи между вершинами
- 67. В ячейках просто указываем веса ребра, а в местах где отсутствует связь пишем 0 или -∞.
- 68. 1. Дайте определение понятию «граф». 2. Назовите области применения графов. 3. Нарисуйте простой неориентированный граф и
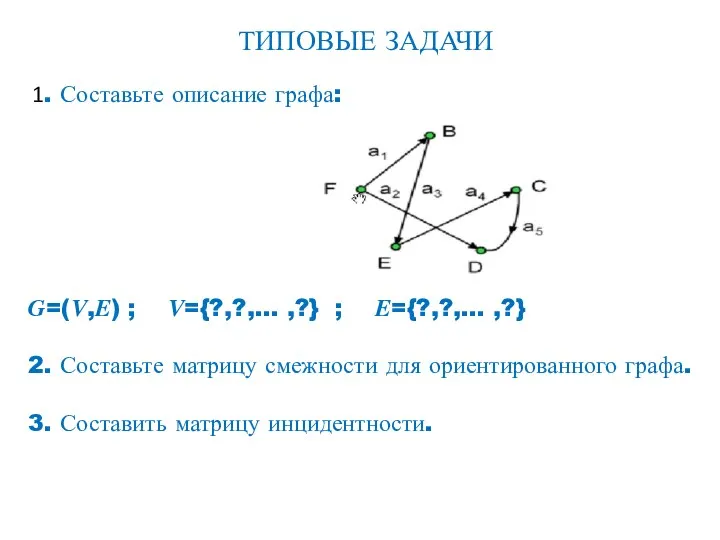
- 69. ТИПОВЫЕ ЗАДАЧИ 1. Составьте описание графа: ?=(?,?) ; ?={?,?,… ,?} ; ?={?,?,… ,?} 2. Составьте матрицу
- 72. ТИПОВЫЕ ЗАДАЧИ Составьте матрицу смежности для графа, заданного списками смежности: A : B, D; B :
- 73. A D B F C E
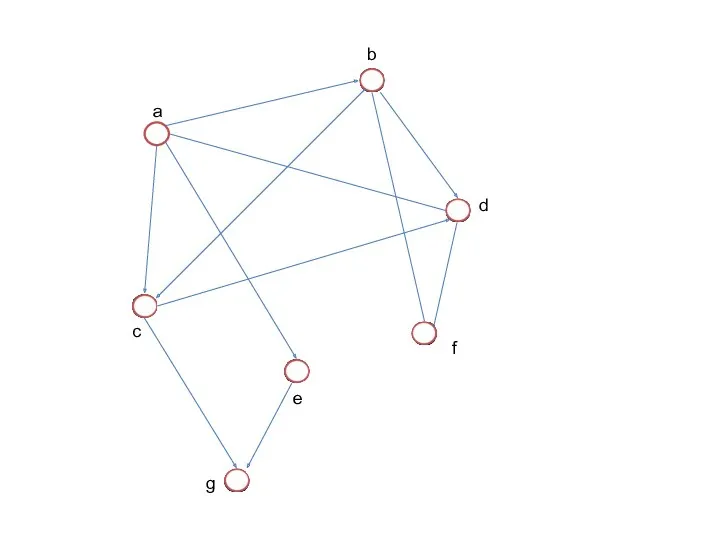
- 75. ТИПОВЫЕ ЗАДАЧИ Постройте матрицу инцидентности для графа, заданного списками смежности: a : b, c, d, e;
- 76. a d b f c e g
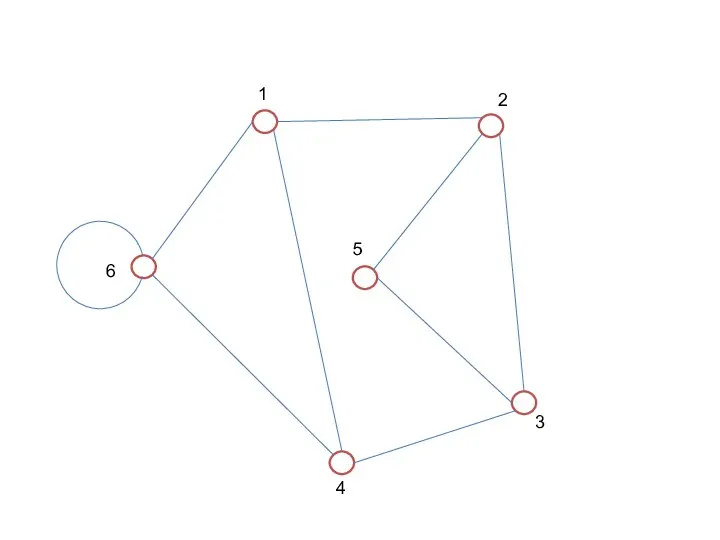
- 77. ТИПОВЫЕ ЗАДАЧИ Дана матрица смежности для неориентированного графа. Составьте граф.
- 78. 1 2 3 4 5 6
- 79. ТИПОВЫЕ ЗАДАЧИ Дана матрица смежности для ориентированного графа. Составьте граф.
- 80. 5 4 3 2 1
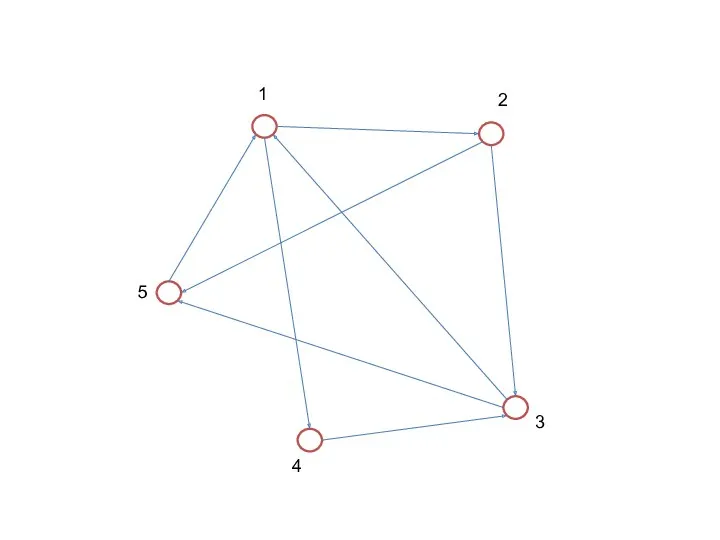
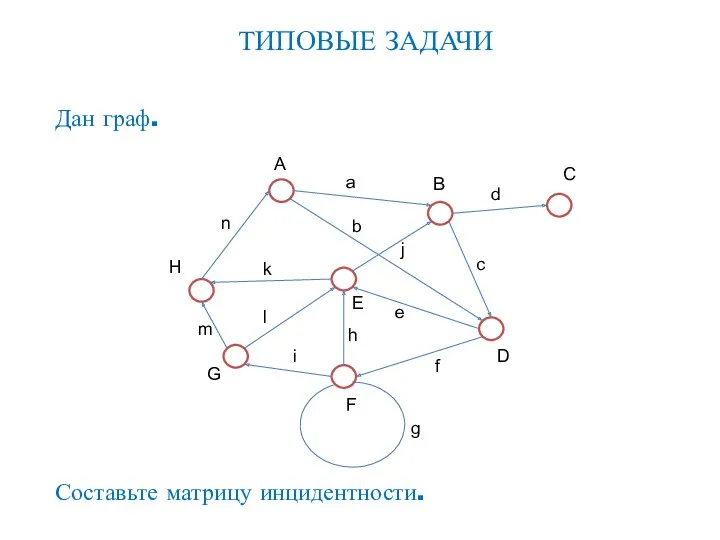
- 81. ТИПОВЫЕ ЗАДАЧИ Дан граф. Составьте матрицу инцидентности. A E H G F D B C a
- 83. Скачать презентацию


































 Четырёхугольники. Виды четырёхугольников. Свойства
Четырёхугольники. Виды четырёхугольников. Свойства Стереометрия. Аксиомы стереометрии
Стереометрия. Аксиомы стереометрии Квадратичные неравенства
Квадратичные неравенства Эконометрическая модель зависимости выручки ПАО Метафракс от внешних факторов
Эконометрическая модель зависимости выручки ПАО Метафракс от внешних факторов Тоновое решение, акценты эскизов. Линия, пятно и линия, пятно
Тоновое решение, акценты эскизов. Линия, пятно и линия, пятно Пифагор. Теорема Пифагора
Пифагор. Теорема Пифагора Счет в пределах 10. Игра Бабочки
Счет в пределах 10. Игра Бабочки Математика. Приклади. Диск
Математика. Приклади. Диск Умножение и деление
Умножение и деление Доба. Замкнені і незамкнені лінії. Повторення вивченого. Урок №28
Доба. Замкнені і незамкнені лінії. Повторення вивченого. Урок №28 Тренажер Порядок действий
Тренажер Порядок действий Нахождение дроби от числа
Нахождение дроби от числа Урок математики в 3 классе Письменные приемы сложения и вычитания трехзначных чисел посвященный Дню Космонавтики.
Урок математики в 3 классе Письменные приемы сложения и вычитания трехзначных чисел посвященный Дню Космонавтики. Урок математики в 1 классе Сложение и вычитание в пределах 20
Урок математики в 1 классе Сложение и вычитание в пределах 20 Предварительный анализ данных. Описательные статистики
Предварительный анализ данных. Описательные статистики Подготовка к контрольной работе. Многогранники
Подготовка к контрольной работе. Многогранники 20231019_kvadratnye_uravneniya_8_klass
20231019_kvadratnye_uravneniya_8_klass Классическое определение вероятности
Классическое определение вероятности Презентация: Геометрические фигуры
Презентация: Геометрические фигуры Применение различных способов для разложения на множители
Применение различных способов для разложения на множители Старинные меры длины
Старинные меры длины Дискретная математика. Основные понятия теории множеств
Дискретная математика. Основные понятия теории множеств كتاب رياضيات و كاربرد آن در مديريت
كتاب رياضيات و كاربرد آن در مديريت Многоугольники. Равные фигуры
Многоугольники. Равные фигуры Решение задач повышенной сложности. (Часть 1)
Решение задач повышенной сложности. (Часть 1) Основные значения тригонометрических функций
Основные значения тригонометрических функций Статистика. Статистическое исследование
Статистика. Статистическое исследование Системы линейных алгебраических уравнений (СЛАУ)
Системы линейных алгебраических уравнений (СЛАУ)