Содержание
- 2. 1. Эллипсоид ОПРЕДЕЛЕНИЕ. Эллипсоидом называется геометрическое место точек пространства, координаты которых в некоторой декартовой системе координат
- 3. Величины a, b и c называются полуосями эллипсоида. Если все они различны, то эллипсоид называется трехостным.
- 4. Эллипсоид, у которого все три полуоси равны, называют сферой. Каноническое уравнение сферы принято записывать в виде
- 5. 2. Гиперболоиды ОПРЕДЕЛЕНИЕ. Однополостным гиперболоидом называется геометрическое место точек пространства, координаты которых в некоторой декартовой системе
- 6. Величины a, b и c называются полуосями однополостного гиперболоида. Если a=b, то однополосный гиперболоид является поверхностью
- 7. ОПРЕДЕЛЕНИЕ. Двуполостным гиперболоидом называется геометрическое место точек пространства, координаты которых в некоторой декартовой системе координат удовлетворяют
- 8. Величины a, b и c называются полуосями двуполостного гиперболоида. Если a=b, то двуполостный гиперболоид является поверхностью
- 9. 3. Конус ОПРЕДЕЛЕНИЕ. Конусом называется геометрическое место точек пространства, координаты которых в некоторой декартовой системе координат
- 10. Величины a, b и c называются полуосями конуса. Центр симметрии O называется вершиной конуса. Если a=b,
- 11. 4. Параболоиды ОПРЕДЕЛЕНИЕ. Эллиптическим параболоидом называется геометрическое место точек пространства, координаты которых в некоторой декартовой системе
- 12. Величины a и b называются параметрами параболоида. Точка O называется вершиной параболоида. Если a=b, то параболоид
- 13. ОПРЕДЕЛЕНИЕ. Гиперболическим параболоидом называется геометрическое место точек пространства, координаты которых в некоторой декартовой системе координат удовлетворяют
- 14. Величины a и b называются параметрами параболоида. Замечания: 1) Уравнение тоже определяет параболоид, но «развернутый» вниз.
- 15. 5. Цилиндры ОПРЕДЕЛЕНИЕ. Цилиндрической поверхностью (цилиндром) называется поверхность, которую описывает прямая (называемая образующей), перемещающаяся параллельно самой
- 17. Скачать презентацию
 Векторная алгебра
Векторная алгебра Нормальные алгоритмы Маркова
Нормальные алгоритмы Маркова Логарифмические выражения
Логарифмические выражения Презентация к уроку математики Повторение 3 класс
Презентация к уроку математики Повторение 3 класс Дополнительные платные образовательные, досуговые и оздоровительные услуги. 2019-2020 учебный год
Дополнительные платные образовательные, досуговые и оздоровительные услуги. 2019-2020 учебный год Методика вивчення рівнянь і нерівностей в основній школі. Методика вивчення систем рівнянь і нерівностей
Методика вивчення рівнянь і нерівностей в основній школі. Методика вивчення систем рівнянь і нерівностей Логические познавательные универсальные учебные действия и приемы анализа текста задачи в геометрии
Логические познавательные универсальные учебные действия и приемы анализа текста задачи в геометрии Математический лабиринт Нить Ариадны
Математический лабиринт Нить Ариадны Формулы
Формулы Презентация Учимся решать задачи 1 класс
Презентация Учимся решать задачи 1 класс Основные понятия дискретной математики. Теория вероятности
Основные понятия дискретной математики. Теория вероятности Счет в пределах 10, 1 класс Зимняя сказка
Счет в пределах 10, 1 класс Зимняя сказка Геометрические фигуры: круг, треугольник, квадрат
Геометрические фигуры: круг, треугольник, квадрат Уравнение. 5 класс. Конкурс
Уравнение. 5 класс. Конкурс Координаты точек пересечения прямых
Координаты точек пересечения прямых Прямая и кривая линии. (1 класс)
Прямая и кривая линии. (1 класс) Контроль динамических систем АО на основе совместных процедур оптимальной фильтрации и сглаживания полетных данных
Контроль динамических систем АО на основе совместных процедур оптимальной фильтрации и сглаживания полетных данных Уроки математики с любимыми героями. Задачи
Уроки математики с любимыми героями. Задачи Обобщающий урок по теме: Деление обыкновенных дробей
Обобщающий урок по теме: Деление обыкновенных дробей Прямоугольные треугольники и некоторые их свойства
Прямоугольные треугольники и некоторые их свойства Линейная алгебра. Матрицы
Линейная алгебра. Матрицы Представление результатов измерений
Представление результатов измерений Застосування математичної статистики у житті
Застосування математичної статистики у житті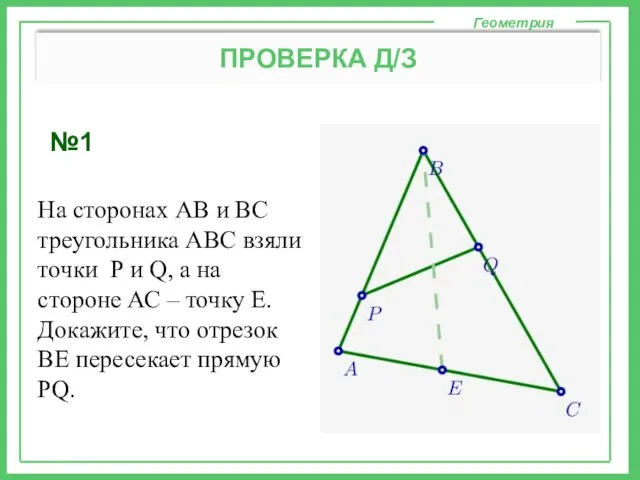 Геометрические фигуры. Элементы фигур
Геометрические фигуры. Элементы фигур Сложение и вычитание смешанных чисел. 5 классе
Сложение и вычитание смешанных чисел. 5 классе Таблица основных углов в тригонометрии
Таблица основных углов в тригонометрии Сложение и вычитание смешанных чисел. 5 класс
Сложение и вычитание смешанных чисел. 5 класс Решение уравнений
Решение уравнений