Содержание
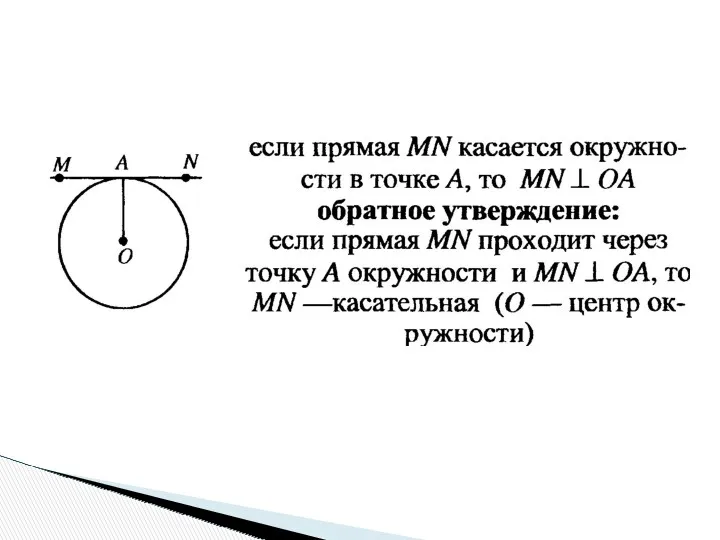
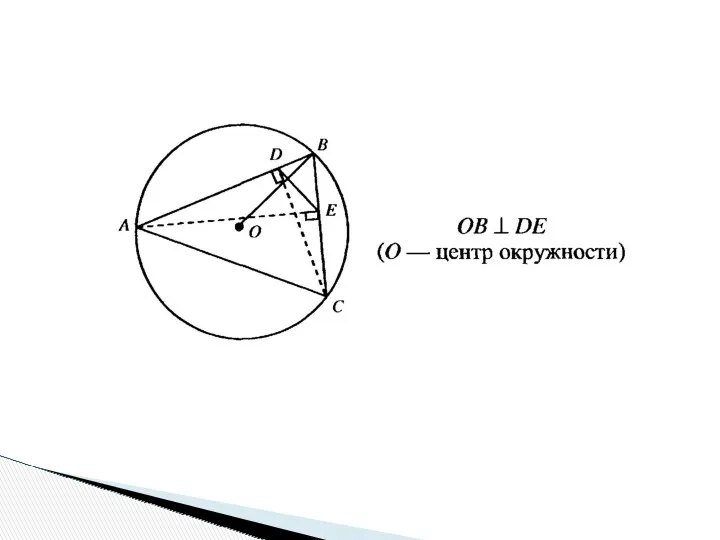
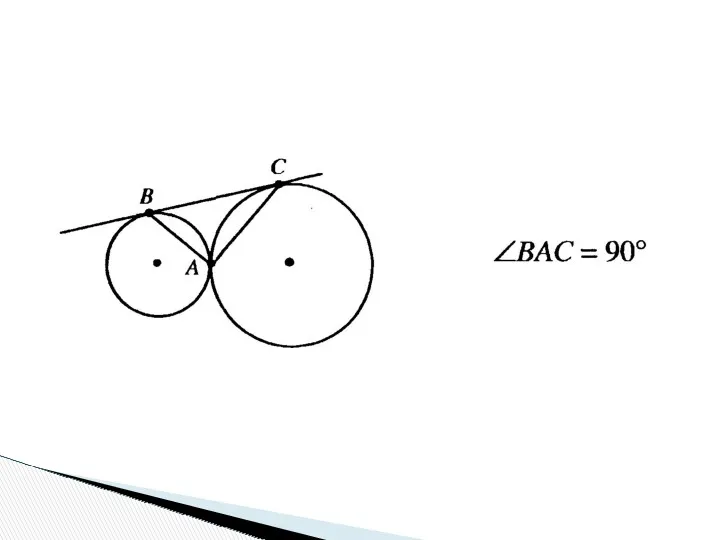
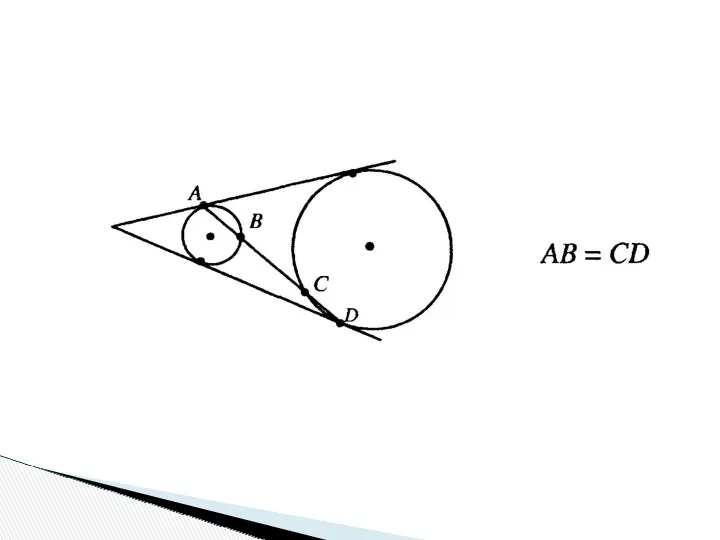
- 23. Опорные задачи
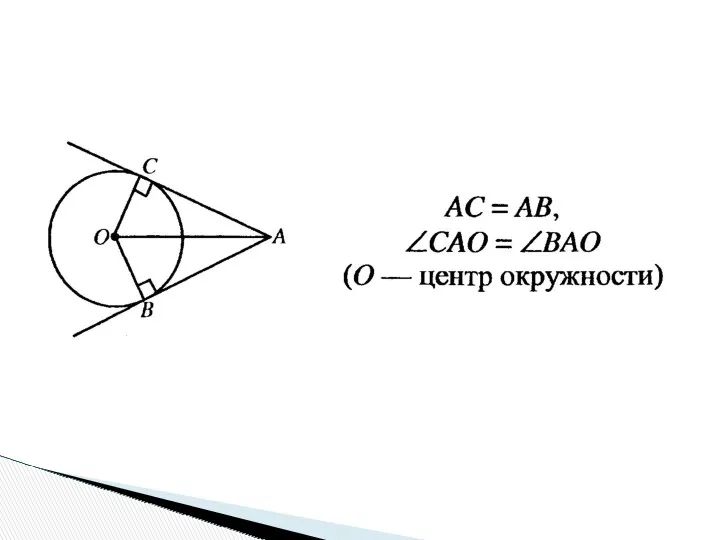
- 24. Опорная задача 1. Прямые АВ и АС – касательные в точках В и С к окружности
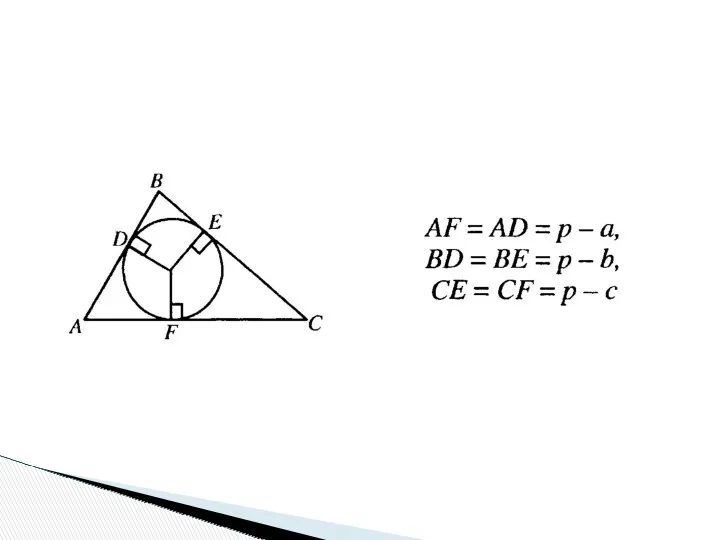
- 25. Опорная задача 2а. В треугольник со сторонами а, b и c вписана окружность, касающаяся стороны АВ
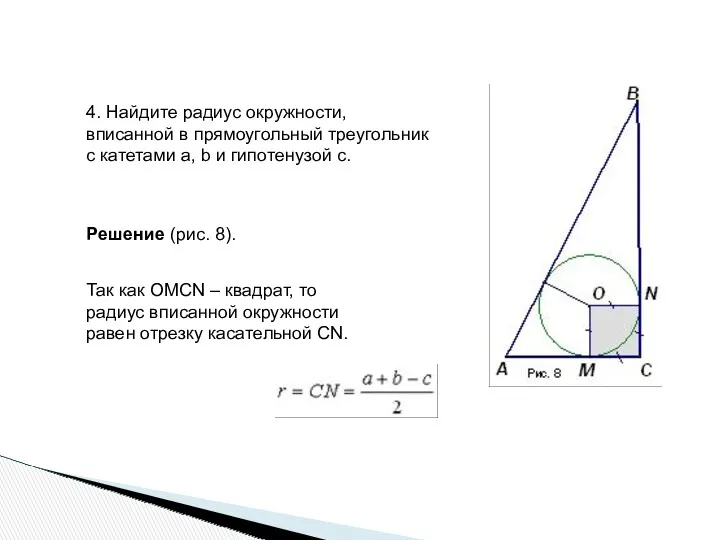
- 26. 4. Найдите радиус окружности, вписанной в прямоугольный треугольник с катетами а, b и гипотенузой с. Так
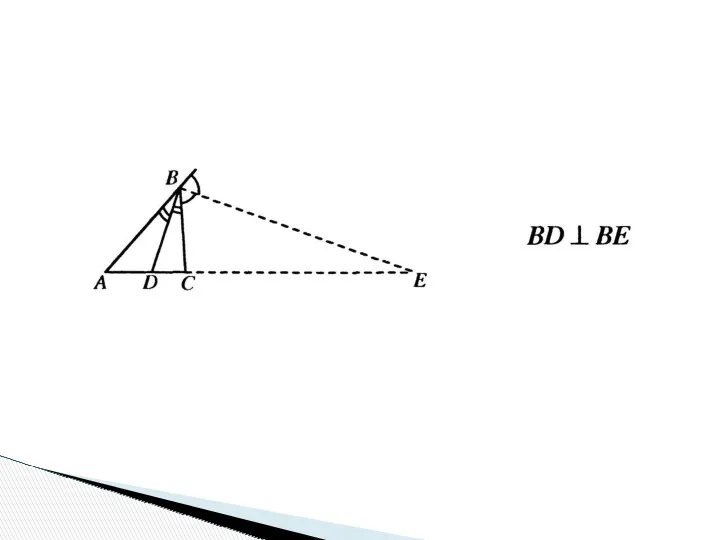
- 27. 5. Докажите, что точки касания вписанной и вневписанной окружности со стороной треугольника симметричны относительно середины этой
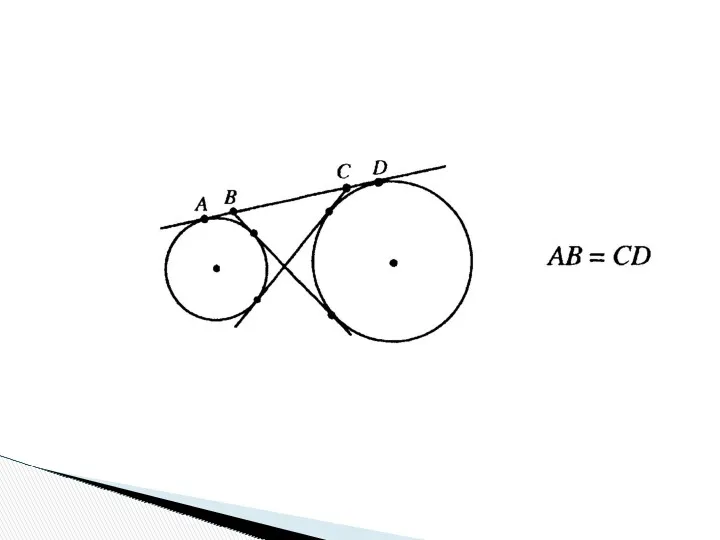
- 28. К двум окружностям проведены две общие внешние касательные и одна внутренняя. Внутренняя касательная пересекает внешние в
- 29. Типовые задачи
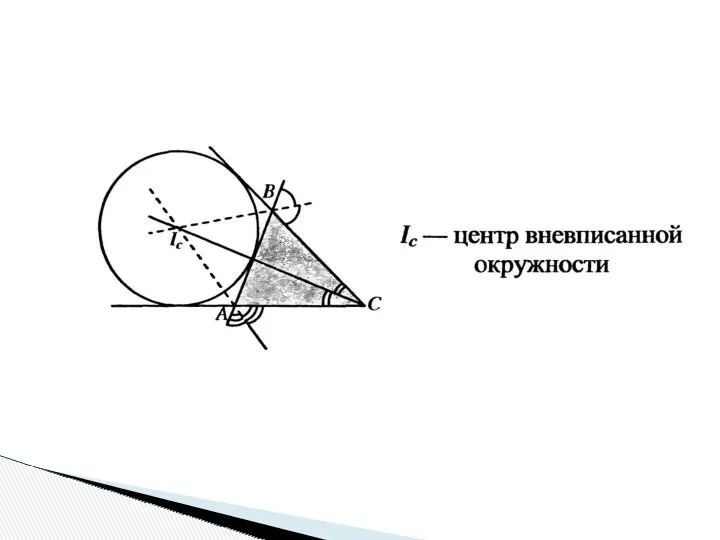
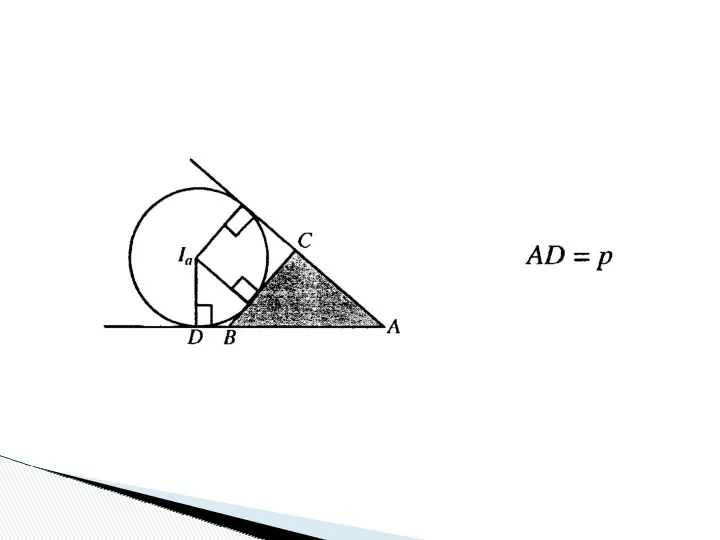
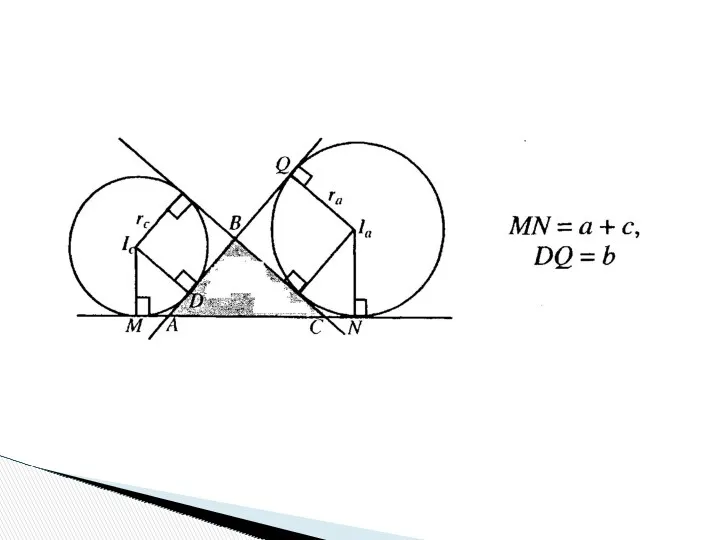
- 30. Вневписанной окружностью треугольника называется окружность, касающаяся одной стороны треугольника и продолжений двух других его сторон. Радиусы
- 32. Пусть теперь (Рис 2) Аналогично предыдущему Получаем, что Возведём в квадрат обе части первого уравнения системы
- 33. Точка О — центр правильного шестиугольника ABCDEF, в котором AC=10.5. Найдите радиус окружности, касающейся окружностей, описанных
- 34. Возможны два случая: либо искомая окружность касается всех трех данных внутренним образом (рис. 1), либо одной
- 35. Рассмотрим второй случай. ПустьQ — центр окружности радиуса x, касающейся внутренним образом описанной окружности треугольника COD
- 37. Скачать презентацию
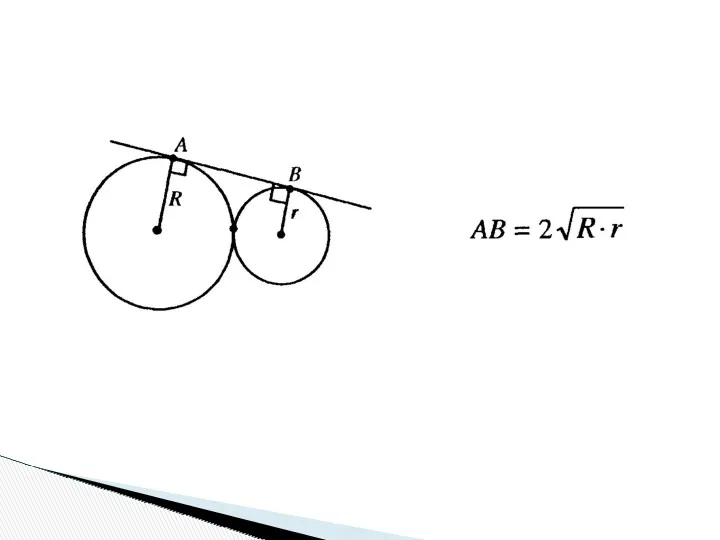

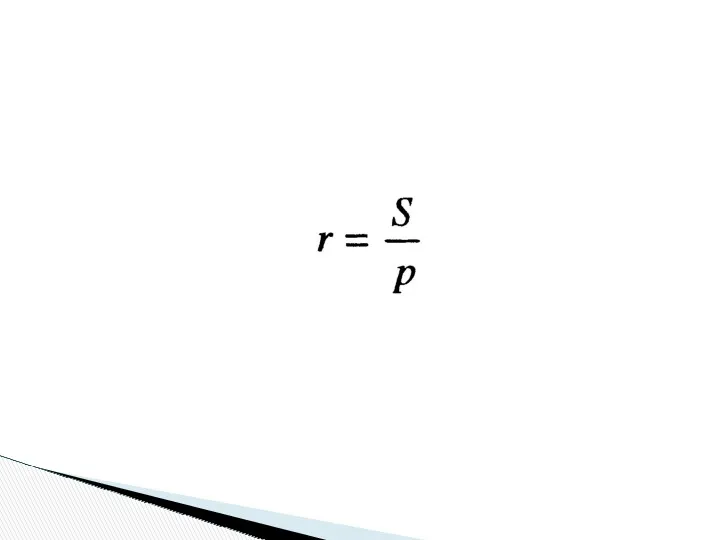
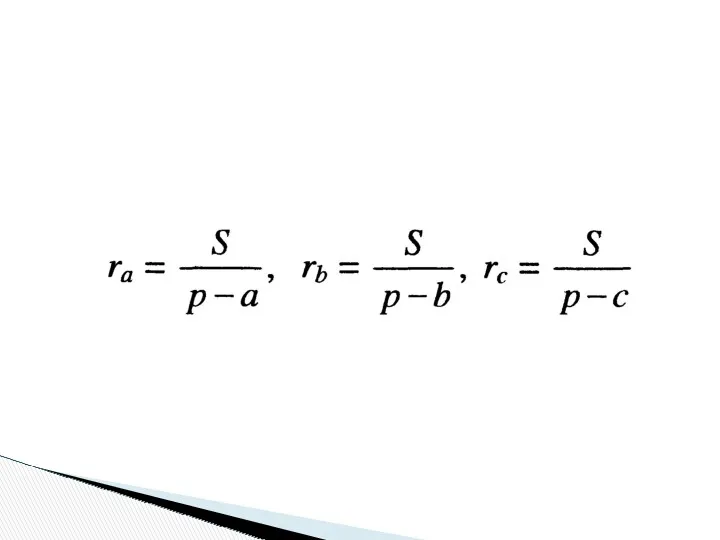
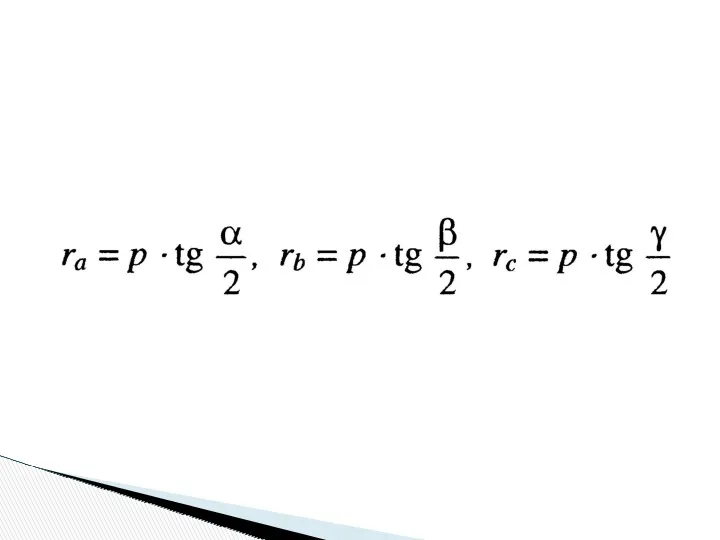












 Урок математики в 1 классе по ФГОС
Урок математики в 1 классе по ФГОС Урок математики во 2 классе Задачи на умножение
Урок математики во 2 классе Задачи на умножение Презентация к уроку Объемные геометрические фигуры
Презентация к уроку Объемные геометрические фигуры Все правила, изучающие в начальной школе
Все правила, изучающие в начальной школе Объём параллелепипеда
Объём параллелепипеда Двузначные числа от 10 до 20
Двузначные числа от 10 до 20 2 класс Туда обратно
2 класс Туда обратно математика
математика Теория вероятностей. Случайные величины
Теория вероятностей. Случайные величины Основы математической логики
Основы математической логики Презентация к уроку Путешествие на остров математики
Презентация к уроку Путешествие на остров математики Следствия из аксиом
Следствия из аксиом Теорема синусов. Теорема косинусов
Теорема синусов. Теорема косинусов Измерение углов. Задания для устного счета. Упражнение 4. 7 класс
Измерение углов. Задания для устного счета. Упражнение 4. 7 класс Юные знатоки физики
Юные знатоки физики Приемы быстрого счета
Приемы быстрого счета График линейного уравнения с двумя неизвестными. Линейное уравнение с двумя переменными
График линейного уравнения с двумя неизвестными. Линейное уравнение с двумя переменными Действия с дробями
Действия с дробями Сonstructive problems and optimization
Сonstructive problems and optimization Следствия из аксиом стереометрии
Следствия из аксиом стереометрии Комбинаторика. Разбор возможных вариантов
Комбинаторика. Разбор возможных вариантов Презентация к уроку Состав числа 10.
Презентация к уроку Состав числа 10. Арифметическая игра Числовые Домики
Арифметическая игра Числовые Домики Геометрические задачи типа 18
Геометрические задачи типа 18 Округление натуральных чисел
Округление натуральных чисел Презентация к уроку математики Космическое путешествие
Презентация к уроку математики Космическое путешествие Урок по математике в 4-м классе по УМК Школа России. По теме: Таблица единиц времени.
Урок по математике в 4-м классе по УМК Школа России. По теме: Таблица единиц времени. Координаты и графики
Координаты и графики