Содержание
- 2. Второй замечательный предел Вторым замечательным пределом называется равенство: Следствия: Другие полезные формулы:
- 3. Второй замечательный предел
- 4. Бесконечно малые функции Бесконечно малые функции часто называют бесконечно малыми величинами; обозначают обычно греческими буквами α,
- 5. Бесконечно малые функции Сравнение бесконечно малых Пусть α(х), β(х) – бесконечно малые функции Если то говорят,
- 6. Бесконечно малые функции Некоторые свойства бесконечно малых Произведение двух бесконечно малых есть бесконечно малая высшего порядка
- 7. Бесконечно малые функции Полезно иметь в виду эквивалентность следующих бесконечно малых при
- 8. Непрерывность функции в точке Пусть функция y = f(x) определена в некоторой окрестности точки x0, и
- 9. Непрерывность функции в точке Так как то равенство (1) можно записать в виде: Это значит, что
- 10. Непрерывность функции в точке Пусть функция y = f(x) определена в некоторой интервале (a; b). Возьмем
- 11. Непрерывность функции в точке х0 y0 Преобразуем равенство (1): Полученное равенство является еще одним определением непрерывности
- 12. Точки разрыва функции Точки, в которых нарушается непрерывность функции, называется точками разрыва функции. Если x =
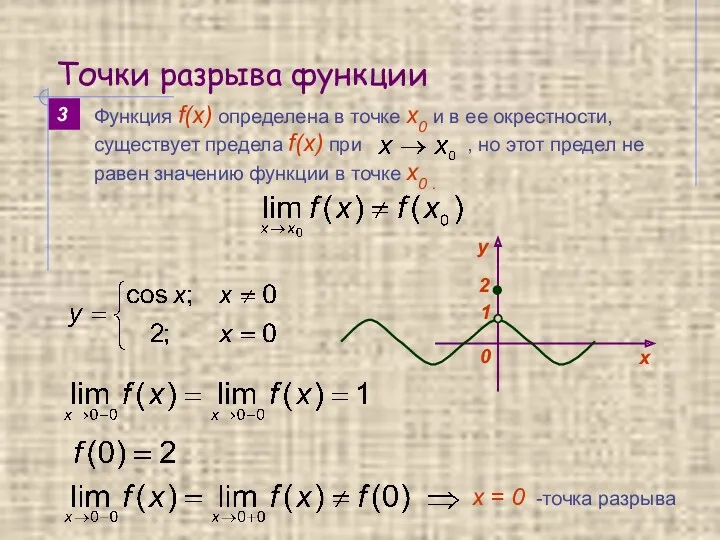
- 13. Точки разрыва функции 2 Функция f(x) определена в точке х0 и в ее окрестности, но не
- 14. Точки разрыва функции 2 3 х = 0 -точка разрыва 1
- 15. Точки разрыва функции Точка разрыва х0 называется точкой разрыва 1 рода функции f(x) , если в
- 16. Точки разрыва функции Точка разрыва х0 называется точкой разрыва 2 рода функции f(x) , если по
- 17. Основные теоремы о непрерывных функциях Сумма, произведение и частное непрерывных функций есть функция непрерывная (для частного
- 18. Непрерывность функции в интервале и на отрезке. Функция y = f(х) называется непрерывной на интервале (a;
- 20. Скачать презентацию
















 Математическая логика в повседневной жизни
Математическая логика в повседневной жизни Определение погрешности измерений
Определение погрешности измерений Формулы сокращенного умнажения
Формулы сокращенного умнажения Квадратный трехчлен. 8 класс
Квадратный трехчлен. 8 класс Презентация к уроку математики в 1 классе по теме Решение простых задач на разностное сравнение, разбиение на группы, составление выражений.
Презентация к уроку математики в 1 классе по теме Решение простых задач на разностное сравнение, разбиение на группы, составление выражений. Проценты в нашей жизни
Проценты в нашей жизни Классификация измерений. Принципы, виды и методы измерений
Классификация измерений. Принципы, виды и методы измерений ЕГЭ профильная математика. Задание № 2. ЕГЭ базовая математика. Задание № 11
ЕГЭ профильная математика. Задание № 2. ЕГЭ базовая математика. Задание № 11 Чёрный ящик. Источник множества интересных математических задач
Чёрный ящик. Источник множества интересных математических задач Основные понятия теории марковских процессов: случайный процесс, марковский процесс, граф состояний, поток событий
Основные понятия теории марковских процессов: случайный процесс, марковский процесс, граф состояний, поток событий Здравствуй, школа! Первые уроки математики в 5 классе
Здравствуй, школа! Первые уроки математики в 5 классе Сложение натуральных чисел и его свойства
Сложение натуральных чисел и его свойства Правильные многогранники
Правильные многогранники Теория вероятностей
Теория вероятностей Геометрическая прогрессия
Геометрическая прогрессия Математика. Закрепление деления многозначного числа на однозначное. 3 класс.
Математика. Закрепление деления многозначного числа на однозначное. 3 класс. Презентация к интегрированному уроку математики и экологии Письменные приемы сложения и вычитания (повторение пройденного)
Презентация к интегрированному уроку математики и экологии Письменные приемы сложения и вычитания (повторение пройденного) математика
математика Центральная и осевая симметрия
Центральная и осевая симметрия Степень с натуральным показателем. Учебная презентация по алгебре для 7 класса
Степень с натуральным показателем. Учебная презентация по алгебре для 7 класса Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание дробей с одинаковыми знаменателями Тройные интегралы. Вычисление тройных интегралов. Декартовы прямоугольные координаты. (Семинар 31)
Тройные интегралы. Вычисление тройных интегралов. Декартовы прямоугольные координаты. (Семинар 31) Математическая игра. 7 класс
Математическая игра. 7 класс Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Оценка точности на основе весов. Теория погрешностей измерений
Оценка точности на основе весов. Теория погрешностей измерений Кушуның урынын алыштыру законы - математика дәресенә презентация
Кушуның урынын алыштыру законы - математика дәресенә презентация Index of Refraction
Index of Refraction Сложение однозначных чисел с переходом через десяток
Сложение однозначных чисел с переходом через десяток