Содержание
- 2. «…нет ни одной области в математике, которая когда-либо не окажется применимой к явлениям действительного мира…» Н.И.
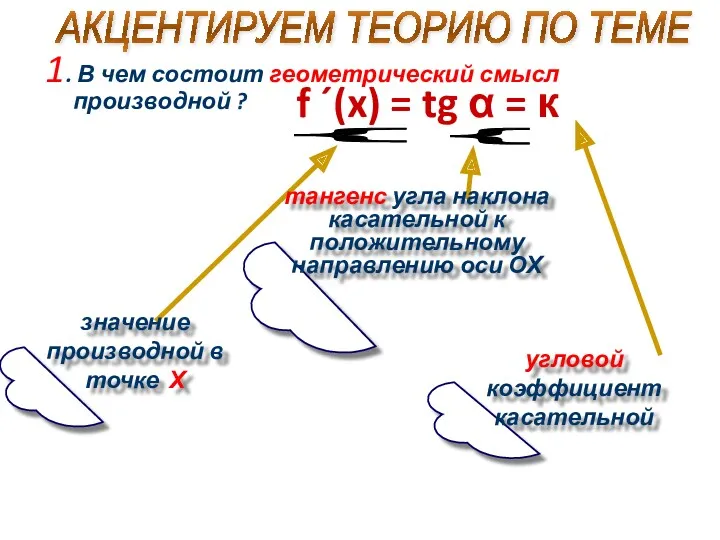
- 3. АКЦЕНТИРУЕМ ТЕОРИЮ ПО ТЕМЕ 1. В чем состоит геометрический смысл производной ? } значение производной в
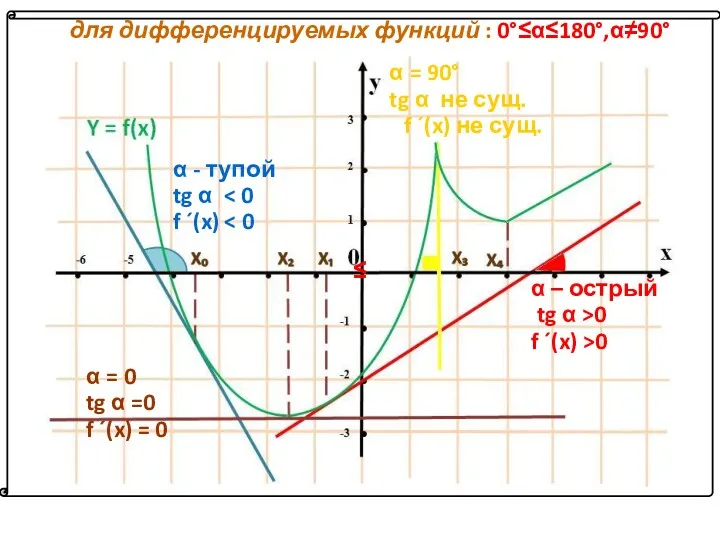
- 4. для дифференцируемых функций : 0°≤α≤180°,α≠90° α - тупой tg α f ´(x) α – острый tg
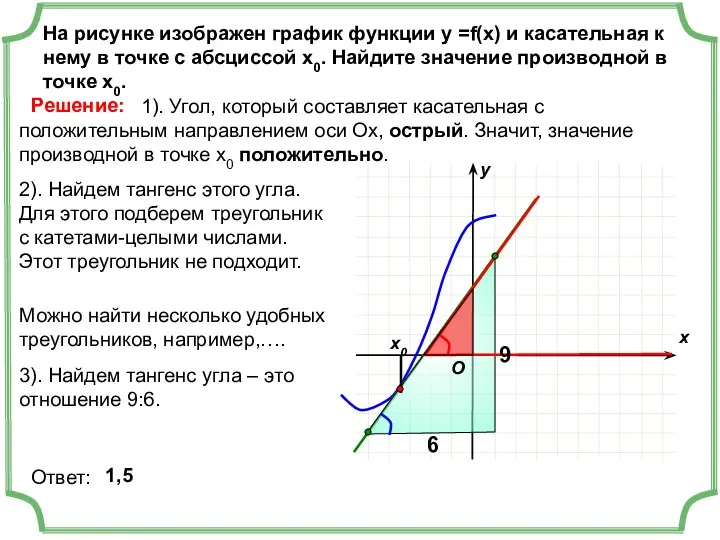
- 5. На рисунке изображен график функции у =f(x) и касательная к нему в точке с абсциссой х0.
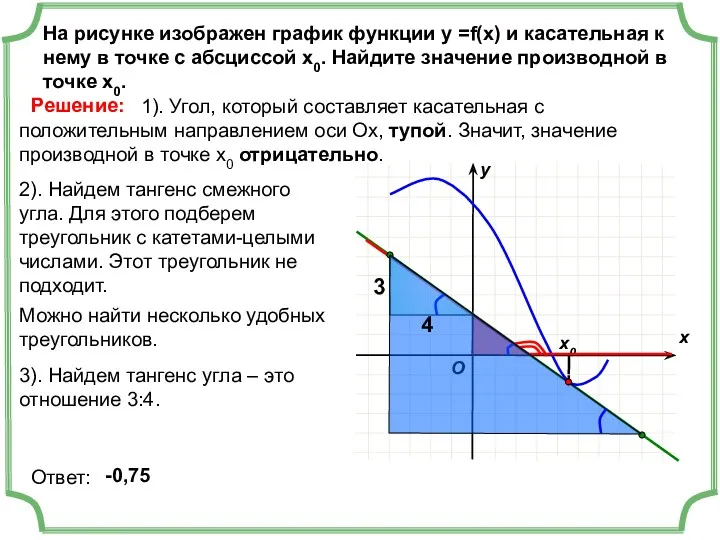
- 6. На рисунке изображен график функции у =f(x) и касательная к нему в точке с абсциссой х0.
- 7. Непрерывная функция у = f(x) задана на отрезке [a;b] На рисунке изображен ее график. y =
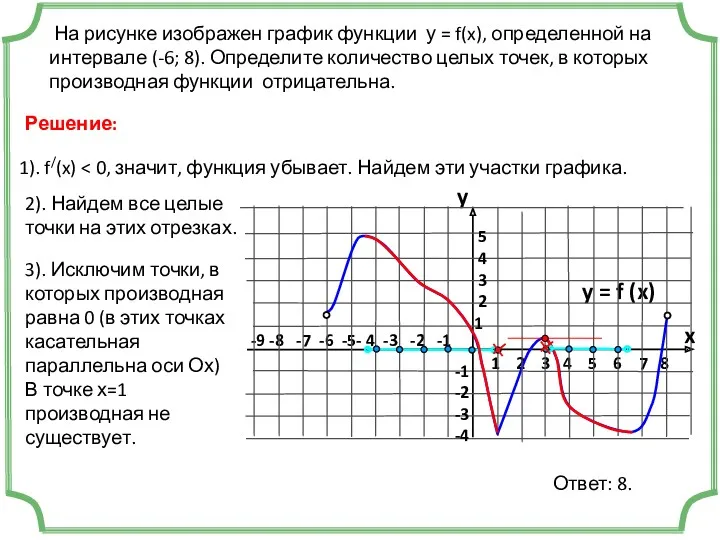
- 8. 3). Исключим точки, в которых производная равна 0 (в этих точках касательная параллельна оси Ох) В
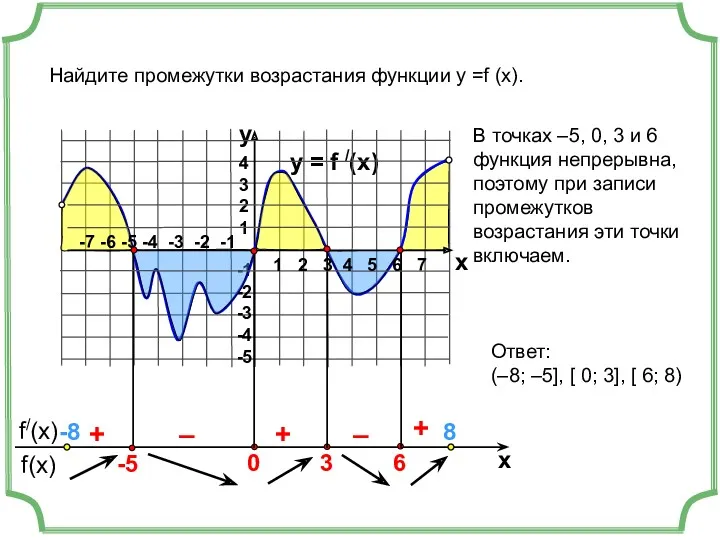
- 9. y = f /(x) 4 3 2 1 -1 -2 -3 -4 -5 y x +
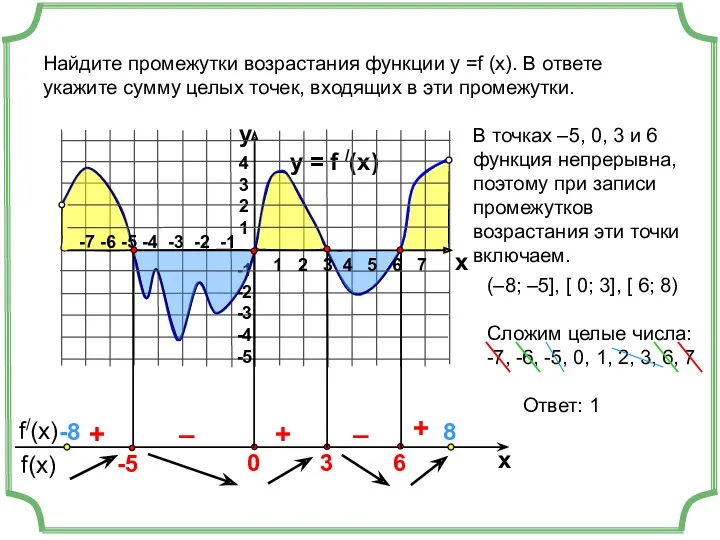
- 10. y = f /(x) 4 3 2 1 -1 -2 -3 -4 -5 y x +
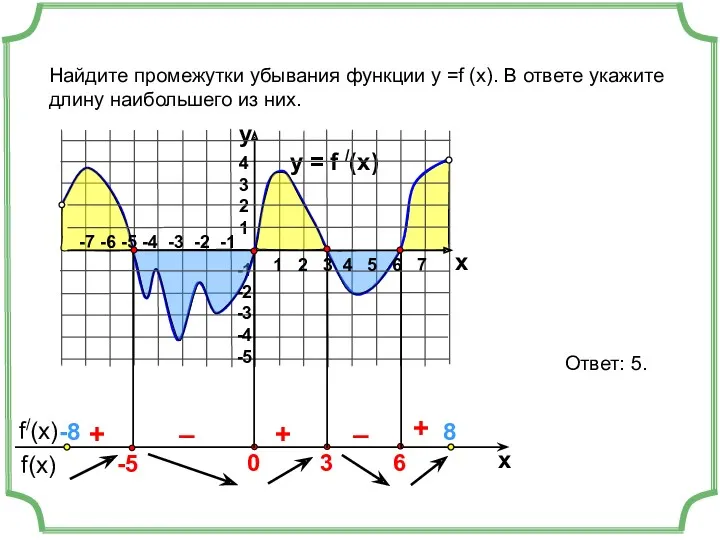
- 11. y = f /(x) 4 3 2 1 -1 -2 -3 -4 -5 y x +
- 12. Связь производной со свойствами функции
- 13. Правило нахождения интервалов монотонности Вычисляем производную f `(x) данной функции f(x). Находим точки, в которых f
- 15. Скачать презентацию

![Непрерывная функция у = f(x) задана на отрезке [a;b] На](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/257857/slide-6.jpg)


 Презентация проекта Юные всезнайки
Презентация проекта Юные всезнайки Открытый урок математики 2 класс Умножение на 2
Открытый урок математики 2 класс Умножение на 2 Свойства аналитических ФКП. Лекция 5
Свойства аналитических ФКП. Лекция 5 Древні математики
Древні математики Упрощение выражений
Упрощение выражений Геометрические характеристики плоских сечений
Геометрические характеристики плоских сечений Урок 12. Числовые характеристики распределения дискретных и непрерывных случайных величин
Урок 12. Числовые характеристики распределения дискретных и непрерывных случайных величин Правильные многоугольники
Правильные многоугольники Окружность и круг. Сфера и шар
Окружность и круг. Сфера и шар Градусная мера дуги окружности. 8 класс
Градусная мера дуги окружности. 8 класс Цилиндр. Определение цилиндра, развёртка цилиндра, формулы для вычисления
Цилиндр. Определение цилиндра, развёртка цилиндра, формулы для вычисления Викторина Своя игра. (10 класс)
Викторина Своя игра. (10 класс) Первый признак равенства треугольников
Первый признак равенства треугольников Компоненты сложения
Компоненты сложения Понятие функции. (7 класс)
Понятие функции. (7 класс) Додавання і віднімання мішаних чисел
Додавання і віднімання мішаних чисел Раскрытие скобок
Раскрытие скобок Именованные числа. Тренажёр
Именованные числа. Тренажёр Наибольшее и наменьшее значения функции на отрезке
Наибольшее и наменьшее значения функции на отрезке Счетный штурманский инструмент. (Тема 5)
Счетный штурманский инструмент. (Тема 5) Решение нестандартных задач
Решение нестандартных задач Цифровой образовательный ресурс по познавательному направлению развития ребенка
Цифровой образовательный ресурс по познавательному направлению развития ребенка Подготовка к контрольной работе по теме Треугольники
Подготовка к контрольной работе по теме Треугольники Занятие по математике в средней группе по теме: Геометрические фигуры
Занятие по математике в средней группе по теме: Геометрические фигуры Побудова графіків тригонометричних функцій
Побудова графіків тригонометричних функцій Машина Тьюринга. Ограничения, свойственные МТ. Рекурсивность и теорема Геделя
Машина Тьюринга. Ограничения, свойственные МТ. Рекурсивность и теорема Геделя Формулы сокращенного умножения. Урок – пресс-конференция
Формулы сокращенного умножения. Урок – пресс-конференция Метод Гаусса систем линейных алгебраических уравнений
Метод Гаусса систем линейных алгебраических уравнений