Содержание
- 2. Цель: Показать актуальность включения темы “Производная и ее применение” в задания для проведения ЕГЭ по математике.
- 3. Задачи: Показать важность знаний исторического и теоретического материала по теме «Производная». Определить процент учащихся, владеющих данным
- 4. План исследования Изучение и отбор литературы. Анализ заданий, рассматриваемых на ЕГЭ по данной теме. Проведение анкетирования
- 5. Гипотеза: Тема «Производная и её применение» является значимой в курсе изучения математики в 10 — 11
- 6. Содержание : 1.Исторические сведения- 7 2.Теоретический материал- 11 - Что такое производная-12 - Как найти производную-
- 7. Исторические сведения В конце 12 века великий английский учёный Исаак Ньютон доказал что путь и скорость
- 8. Честь открытия основных законов математического анализа наравне с Ньютоном принадлежит немецкому математику Готфриду Вильгельму Лейбницу. К
- 9. Термин производная и современные обозначения y’ , f ’ ввёл Ж.Лагранж в 1797г. В классическом дифференциальном
- 10. Василий Иванович Висковатов (26 декабря 1779 (6 января 1780), Санкт-Петербург — 8 (20) октября 1812, Санкт-Петербург)
- 11. Теоретический материал по теме «ПРОИЗВОДНАЯ»
- 12. Производные - это такие функции, которые получаются из заданных функций путем вычисления предела разностного отношения. Разностным
- 13. Как найти производную? 1. Необходимо знать таблицу производных основных элементарных функций. 2. Уметь видеть, как составная
- 14. Таблица производных
- 15. Производная произведения. Формула Формула производной произведения читается следующим образом: производная произведения двух функций равна сумме произведений
- 16. Берем второй сомножитель, а точнее - его производную: (sin(x))' Умножаем производную второго сомножителя на первый сомножитель
- 17. Производная частного функций Формула производная частного, формула производной отношения двух функций записывается следующим образом: [u(x)/v(x)]'=[u'(x)·v(x)-u(x)·v'(x)]·[1/v2(x)] Итак
- 18. Далее, подставляем уже известные выражения производных числителя и знаменателя и упрощаем выражение полученной производной: [(√x)'·x2-(√x)·(x2)']·[1/(x2)2]=[(1/2√x)·x2-(√x)·2x]·[1/(x2)2]=[(1/2x½)·x2-(x½)·2x]·[1/(x2)2]=[½·x(2-½)-2·x2+½]·[1/x4]=[½·x3/2-2·x3/2]·[1/x4]=-[(3/2)·x3/2]·[1/x4]=-(3/2)·x-5/2 Здесь
- 19. ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ ПРОСТЫХ ФУНКЦИЙ Пример 1. Комментарий. После применения теоремы о производной суммы (Теорема 3) образовалось
- 20. Пример 2. Комментарий. После применения теорема о производной произведения (ТЕОРЕМА 4) возникло две производных. Первая производная
- 21. Пример 3. Комментарий. После применения теоремы о производной частного (ТЕОРЕМА 5) образовалось две производных. Вторая производная
- 22. ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ СЛОЖНЫХ ФУНКЦИЙ Пример 1. Вычислить производную от функции Данную функцию можно представить как функцию
- 23. Теорема 2. Константу можно вынести за знак производной, то есть назад
- 24. Теорема 3. Производная суммы любого числа функций равна сумме производных этих функций. Для трех функций, например,
- 25. Теорема 4. Производная произведения двух функций равна назад
- 26. Теорема 5. Производная частного двух функций равна назад
- 27. Теорема 6. Пусть y=F(u), где u=j(x), тогда назад
- 28. В11 Найдите точку максимума функции Задачи для дополнительного решения Найдите точку минимума функции Решение: Найдём производную
- 29. Анкетирование учащихся 1.Запишите формулы нахождения производных Линейной функции; Степенной функции; Тригонометрической функции; Сложной функции; Логарифмической функции.
- 30. В11 Найдите точку максимума функции Задачи для дополнительного решения Найдите точку минимума функции Решение: Найдём производную
- 31. В11 Найдите точку максимума функции Задачи для дополнительного решения Найдите точку минимума функции Решение: Найдём производную
- 32. Задания из сборников по подготовке к ЕГЭ
- 33. В8 На рисунке изображены график функции и касательная к нему в точке с абсциссой . Найдите
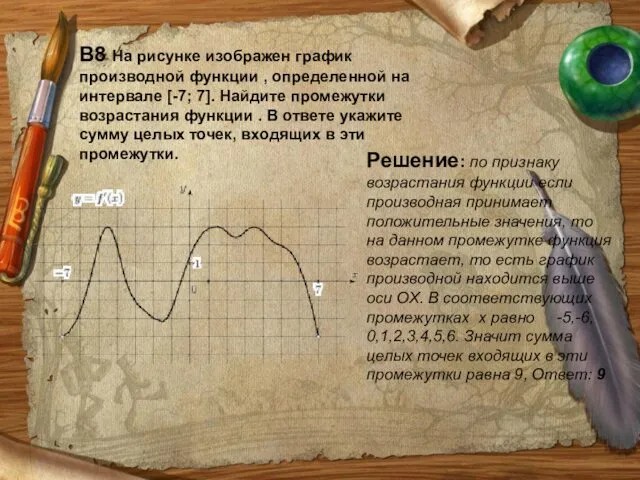
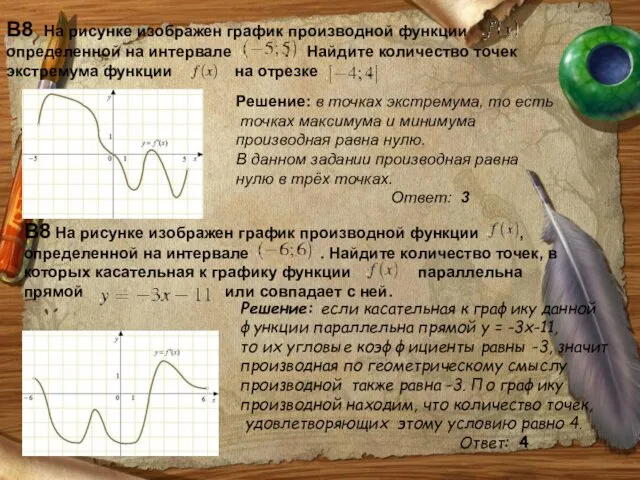
- 34. В8 На рисунке изображен график производной функции , определенной на интервале [-7; 7]. Найдите промежутки возрастания
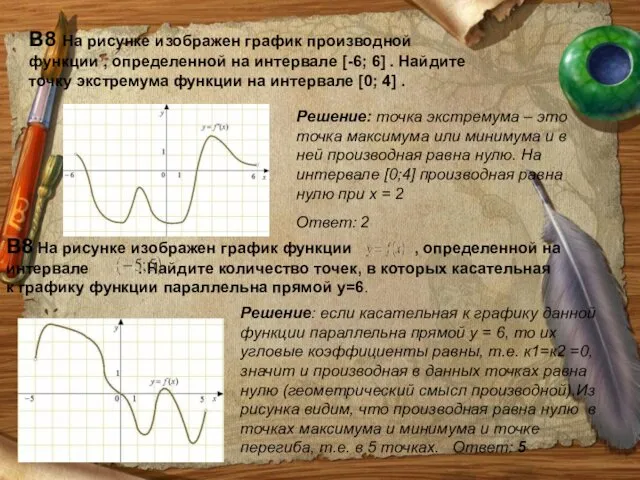
- 35. В8 На рисунке изображен график производной функции , определенной на интервале [-6; 6] . Найдите точку
- 36. В8 На рисунке изображен график функции , определенной на интервале . Определите количество целых точек, в
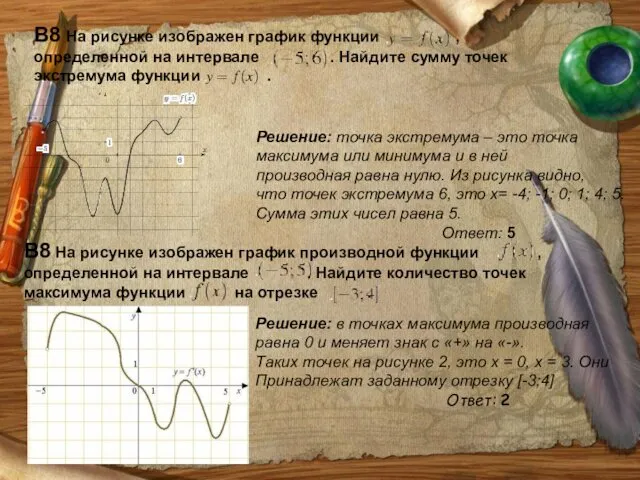
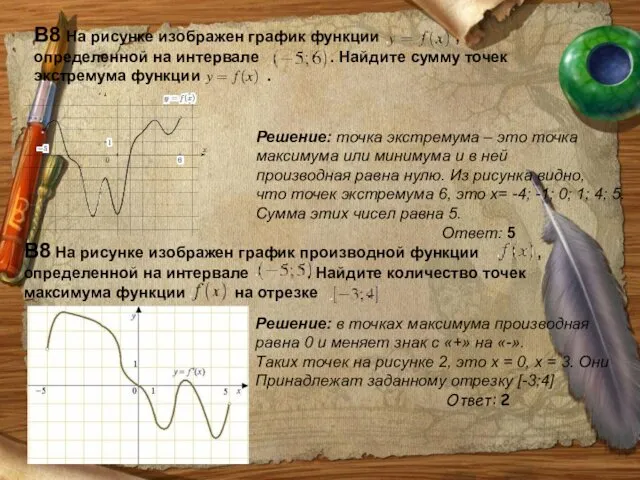
- 37. В8 На рисунке изображен график функции , определенной на интервале . Найдите сумму точек экстремума функции
- 38. В8 На рисунке изображен график функции , определенной на интервале . Найдите сумму точек экстремума функции
- 39. В8 На рисунке изображен график производной функции определенной на интервале . Найдите количество точек экстремума функции
- 40. Задачи для самостоятельного решения В11. Найдите точку минимума функции . В11. Найдите точку максимума функции .
- 41. В11 Найдите точку максимума функции Задачи для дополнительного решения Найдите точку минимума функции Решение: Найдём производную
- 42. Заключение Данная работа показывает: что тема «Производная и ее применение» актуальна и значима в настоящее время.
- 44. Скачать презентацию




































 Деление на трехзначное число
Деление на трехзначное число Отрезок. Треугольник. Многоугольники
Отрезок. Треугольник. Многоугольники Классификация экономико-математических моделей
Классификация экономико-математических моделей Цилиндр. Определение цилиндра
Цилиндр. Определение цилиндра Ломаные и многоугольники
Ломаные и многоугольники Додавання і віднімання числа 3. Переставний закон додавання. Урок №38. Математика
Додавання і віднімання числа 3. Переставний закон додавання. Урок №38. Математика Презентация Деление с остатком
Презентация Деление с остатком Порядок выполнения действий в выражениях
Порядок выполнения действий в выражениях Урок-соревнование для пятиклассников. Натуральные числа
Урок-соревнование для пятиклассников. Натуральные числа Деление с остатком
Деление с остатком презентация к уроку математики на тему Алгоритм письменного деления. Прикидка результата.Сравнение выражений.
презентация к уроку математики на тему Алгоритм письменного деления. Прикидка результата.Сравнение выражений. Математика в гимнастике
Математика в гимнастике Решение задач с помощью уравнений
Решение задач с помощью уравнений система координат на плоскости
система координат на плоскости презентация к уроку №83
презентация к уроку №83 Арифметичні дії з іменованими числами математика
Арифметичні дії з іменованими числами математика Решение приведённых квадратных уравнений
Решение приведённых квадратных уравнений Графический метод решения системы уравнений с двумя переменными. 7 класс
Графический метод решения системы уравнений с двумя переменными. 7 класс Лекция 2 по статистике. Основные категории и понятия статистики
Лекция 2 по статистике. Основные категории и понятия статистики Площади многоугольников
Площади многоугольников Функцияның туындысы нольге тең немесе туындысы болмайтын анықталу облысының ішкі нүктелері сындық нүктелер деп атайды
Функцияның туындысы нольге тең немесе туындысы болмайтын анықталу облысының ішкі нүктелері сындық нүктелер деп атайды Түзу мен жазықтық арасындағы бұрыш
Түзу мен жазықтық арасындағы бұрыш Тест по теме Умножение натуральных чисел
Тест по теме Умножение натуральных чисел Текстовая задача и процесс ее решения
Текстовая задача и процесс ее решения Структурные схемы и их преобразование. Типовые динамические звенья САУ и их классификация
Структурные схемы и их преобразование. Типовые динамические звенья САУ и их классификация Наибольший общий делитель
Наибольший общий делитель Пропорции
Пропорции Признаки параллельных прямых. 7 класс
Признаки параллельных прямых. 7 класс