Содержание
- 2. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ Задачи, приводящие к понятию производной
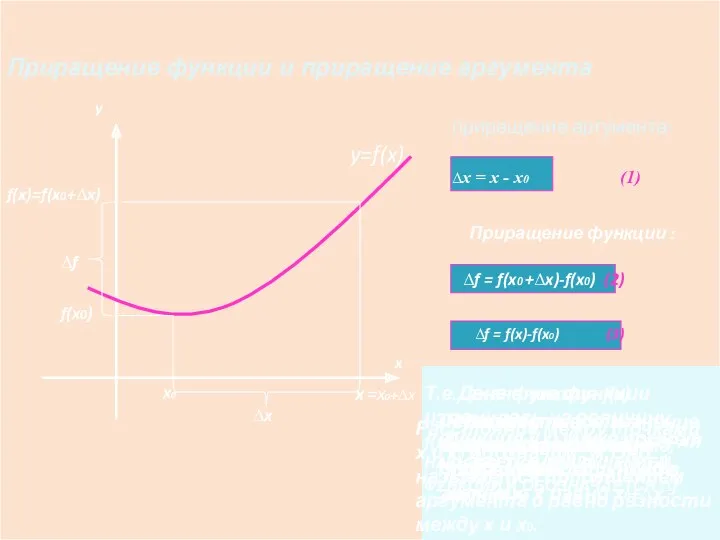
- 3. =x0+∆x Приращение функции и приращение аргумента y=f(x) x0 f(x)=f(x0+∆x) f(x0) ∆x ∆f приращение аргумента: x y
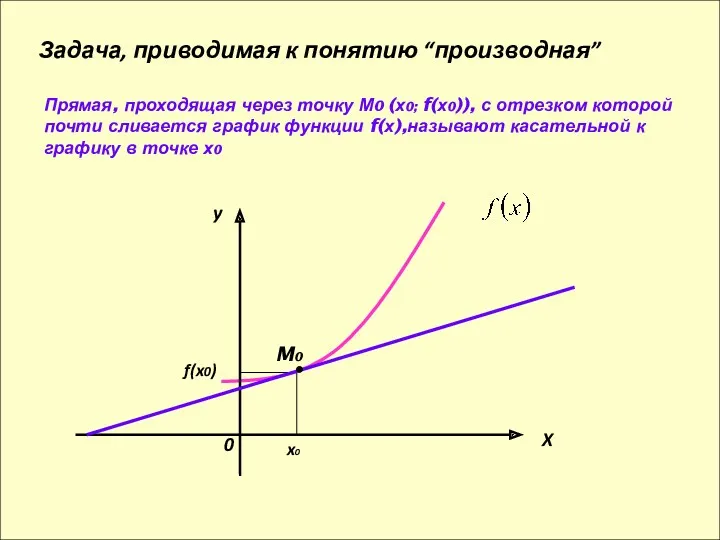
- 4. Прямая, проходящая через точку М0 (х0; f(х0)), с отрезком которой почти сливается график функции f(х),называют касательной
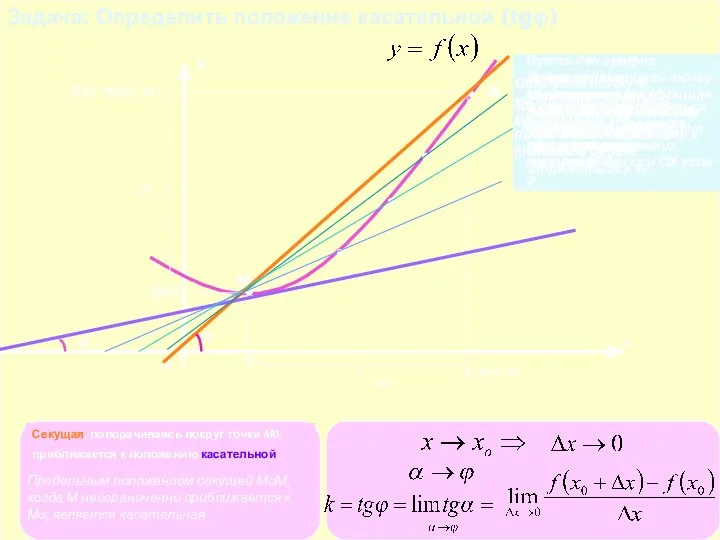
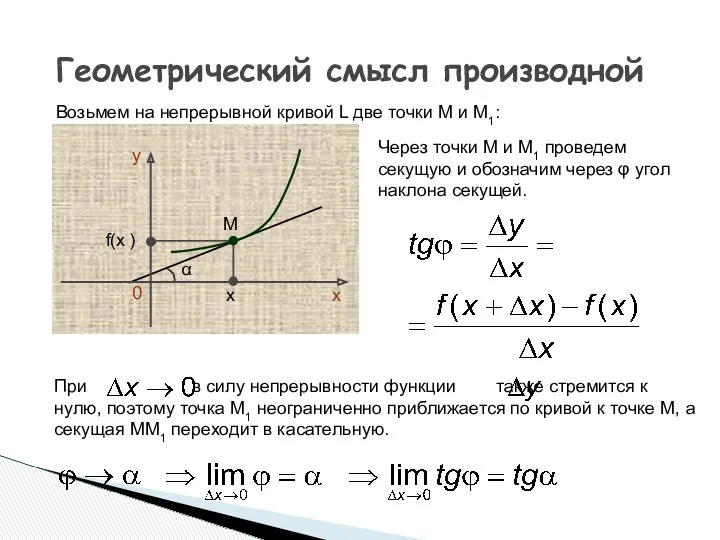
- 5. Задача: Определить положение касательной (tgφ) х у 0 М0 х0 f(x0) М х f(x) =x0+∆x ∆x
- 6. Определение производной Производной функции f в точке х0 называется предел отношения приращения функции к приращению аргумента
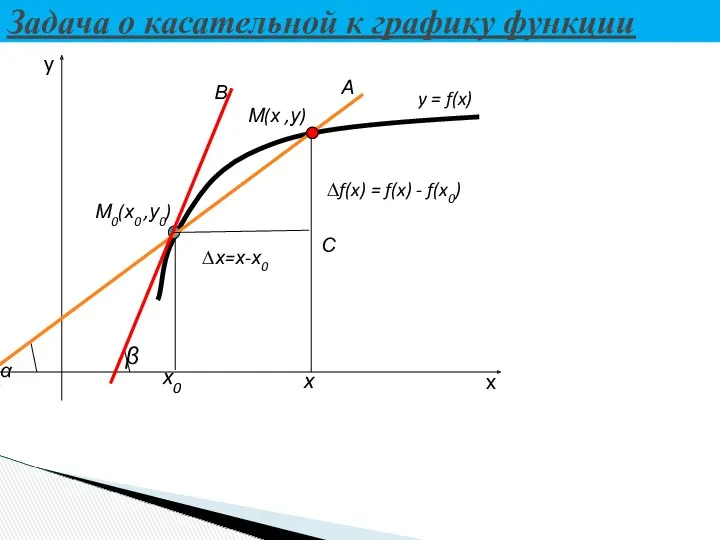
- 7. Задача о касательной к графику функции x y С ∆х=х-х0 ∆f(x) = f(x) - f(x0)
- 8. Физический смысл производной x`(t) от непрерывной функции x(t) в точке t (0) – есть мгновенная скорость
- 9. - Представьте, что вы летите в самолёте и у вас на руке часы. Когда Вы летите,
- 12. Геометрический смысл производной Возьмем на непрерывной кривой L две точки М и М1: х f(x )
- 13. Геометрический смысл производной Производная f ’(x) равна угловому коэффициенту касательной к графику функции y = f(x)
- 14. Уравнение касательной f(x)= f (x0)+ f ´(x0)(x- x0) Kоэффициент угла наклона касательной k = f ´(x0)
- 15. (f(х) ± g( х))΄= (Сf(х))΄= (f(х)·g( х))΄= (f(х)/g(х))΄= Правило вычисления производных. f(х)΄± g( х)΄ С( f(х))΄
- 16. g (f(x ))΄ = Производная сложной функции. g΄(f(x))·f ΄(x)
- 17. Основные формулы k 0 1 1/х
- 18. Производные тригонометрических функций. (sin x) ΄ = (cos x) ΄ = (tg x) ΄ = (ctg
- 19. Связь между непрерывностью и дифференцируемостью функции Если функция f(x) дифференцируема в некоторой точке , то она
- 20. Производные основных элементарных функций 1 Формула бинома Ньютона: Степенная функция: K – факториал
- 21. Производные основных элементарных функций По формуле бинома Ньютона имеем: Тогда:
- 22. Производные основных элементарных функций 2 Логарифмическая функция: Аналогично выводятся правила дифференцирования других основных элементарных функций.
- 23. Правила дифференцирования Пусть u(x) , v(x) и w(x) – дифференцируемые в некотором интервале (a; b) функции,
- 25. Скачать презентацию

















 Скалярное произведение векторов
Скалярное произведение векторов Презентация Умножение двузначного числа на однозначное 3 класс Планета знаний
Презентация Умножение двузначного числа на однозначное 3 класс Планета знаний Все действия с дробями. Урок математики в 5 классе
Все действия с дробями. Урок математики в 5 классе Презентация Молчанка (устный счет, 4 класс)
Презентация Молчанка (устный счет, 4 класс) Линейная функция и её график
Линейная функция и её график Презентация Математика вокруг нас
Презентация Математика вокруг нас Вычесть число 3.
Вычесть число 3. Понятие определенного интеграла
Понятие определенного интеграла Сызықтық емес (бейсызықтық) жұп регрессия
Сызықтық емес (бейсызықтық) жұп регрессия Дроби. Нахождение части числа. Нахождение целого по его части.
Дроби. Нахождение части числа. Нахождение целого по его части. Решение логических задач
Решение логических задач Знаходження невідомого зменшуваного
Знаходження невідомого зменшуваного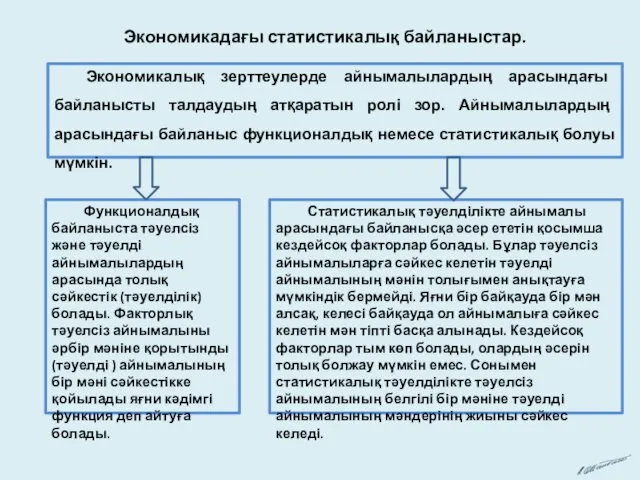 Экономикадағы статистикалық байланыстар
Экономикадағы статистикалық байланыстар Памятка по оформлению краткой записи к задачам
Памятка по оформлению краткой записи к задачам Квадратные неравенства
Квадратные неравенства Тема урока: знаки > (больше), < (меньше)Математика 1 класс Диск
Тема урока: знаки > (больше), < (меньше)Математика 1 класс Диск Алгоритмические структуры
Алгоритмические структуры Обчислення виду 13 + 2. Задачі різних типів з одним сюжетом. Урок №81
Обчислення виду 13 + 2. Задачі різних типів з одним сюжетом. Урок №81 Решение уравнений (6 класс)
Решение уравнений (6 класс) Утворення, запис, читання чисел
Утворення, запис, читання чисел Единицы массы: тонна и центнер
Единицы массы: тонна и центнер Понятие алгоритма действий
Понятие алгоритма действий Симметрия в пространстве. Симметрия в природе и на практике
Симметрия в пространстве. Симметрия в природе и на практике Урок -викторина Счастливый случай. Параллельные прямые
Урок -викторина Счастливый случай. Параллельные прямые Графическое решение квадратных уравнений
Графическое решение квадратных уравнений Разработка открытого урока математики
Разработка открытого урока математики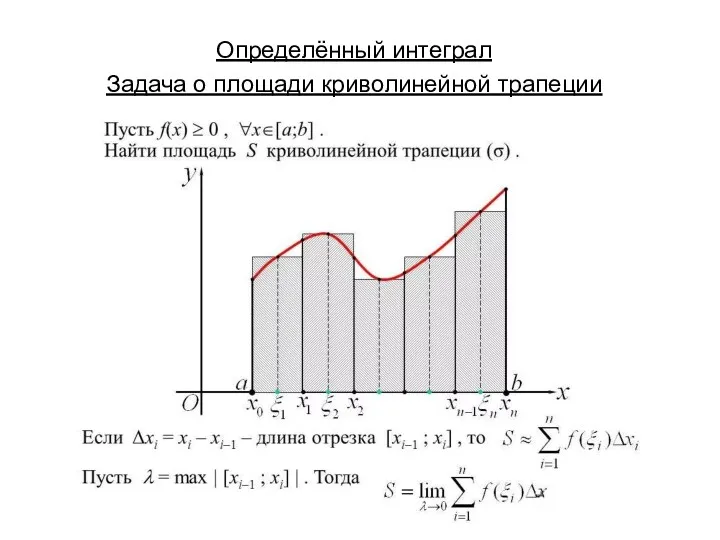 Определённый интеграл. Задача о площади криволинейной трапеции
Определённый интеграл. Задача о площади криволинейной трапеции Подготовка к ОГЭ. Методы, способствующие решению геометрических задач
Подготовка к ОГЭ. Методы, способствующие решению геометрических задач