Содержание
- 2. Содержание Задача о касательной Общее определение производной Зависимость между непрерывностью и дифференцируемостью функции Основные правила Дифференцирования
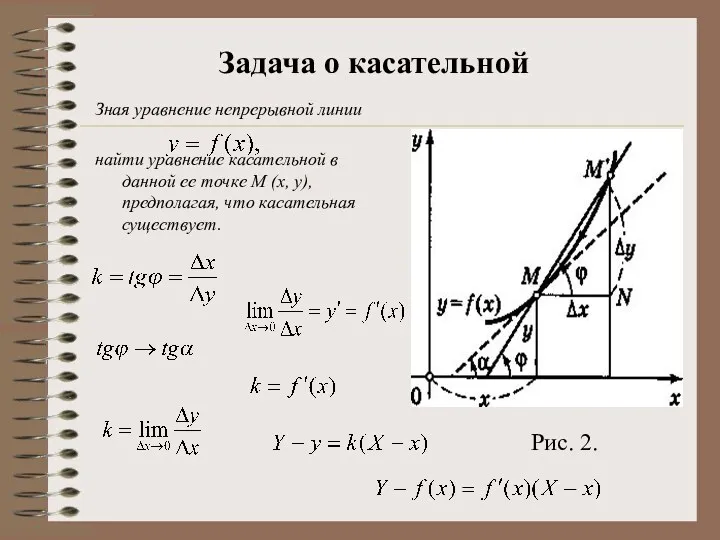
- 3. Касательной к данной непрерывной кривой в данной ее точке М (точка касания) называется предельное положение секущей
- 4. Зная уравнение непрерывной линии найти уравнение касательной в данной ее точке М (х, у), предполагая, что
- 5. Задача о скорости движения Задача. Зная закон движения S=f(t), найти скорость движущейся точки для любого момента
- 6. Общее определение производной Производной функции у = f(х) называется предел отношения приращения функции к приращению аргумента
- 7. Смысл производной Физический Геометрический Например касательной к графику функции y=f (x) в точке, абсцисса которой равна
- 8. Мы видели, что функция называется непрерывной в точке х, если в этой точке Функция называется дифференцируемой
- 9. Если функция дифференцируема в некоторой точке, то в этой точке функция непрерывна. Обратное утверждение неверно: непрерывная
- 10. I. Производная постоянной величины равна нулю. Основные правила дифференцирования функций: II. Производная алгебраической суммы конечного числа
- 11. Если у = f(z)и z= (x)— дифференцируемые функции от своих аргументов, то производная сложной функции существует
- 12. Производная обратной функции ТЕОРЕМА. Для дифференцируемой функции с производной, не равной нулю, производная обратной функции равна
- 13. Если y как функция от x задается соотношением F(x, y)=0, где F(x, y) - выражение, содержащее
- 14. Производная функции, заданной параметрически Если функция у от аргумента х задана параметрически и где функции и
- 15. Понятие о производных высших порядков Производная f '(х) от функции f (х) называется производной первого порядка
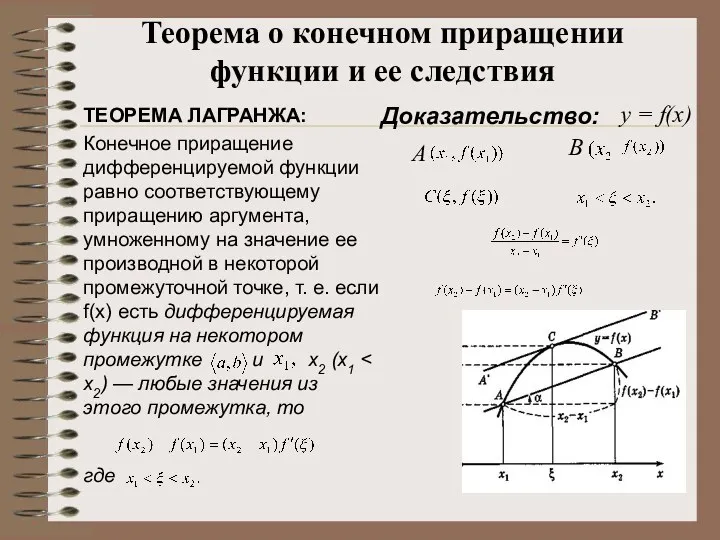
- 16. Доказательство: Конечное приращение дифференцируемой функции равно соответствующему приращению аргумента, умноженному на значение ее производной в некоторой
- 17. Доказательство: В самом деле, если f(х) — дифференцируемая функция и то из формулы имеем или, так
- 18. Если функция y=f (х) определена и непрерывна (a, b) и пусть эта функция принимает max во
- 19. Возрастание и убывание функции одной переменной 1) Если дифференцируемая функция возрастает в некотором промежутке, то производная
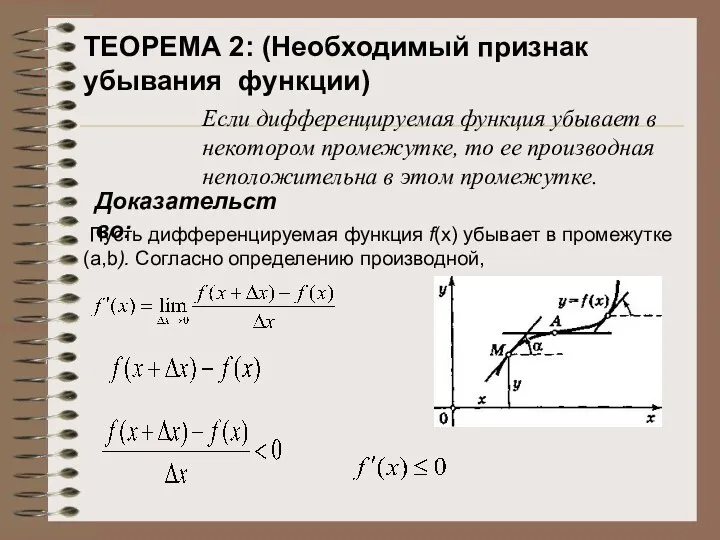
- 20. Если дифференцируемая функция убывает в некотором промежутке, то ее производная неположительна в этом промежутке. Пусть дифференцируемая
- 21. 1) Если производная дифференцируемой функции положительна внутри некоторого промежутка, то функция возрастает на этом промежутке. ТЕОРЕМА:
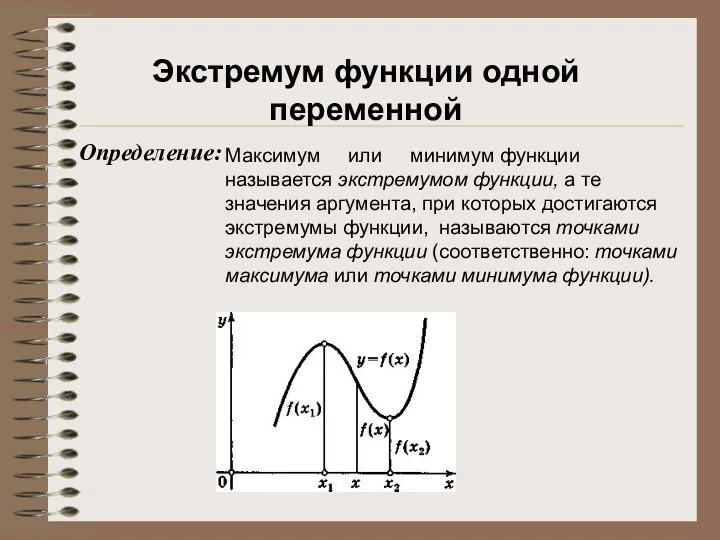
- 22. Максимум или минимум функции называется экстремумом функции, а те значения аргумента, при которых достигаются экстремумы функции,
- 23. НЕОБХОДИМОЕ УСЛОВИЕ ЭКСТРЕМУМА ФУНКЦИИ ТЕОРЕМА. В точке экстремума (двустороннего) дифференцируемой функции производная ее равна нулю. Доказательство.
- 24. ДОСТАТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМА ФУНКЦИИ ТЕОРЕМА: Если дифференцируемая функция f(х) такова, что для некоторого значения ее аргумента
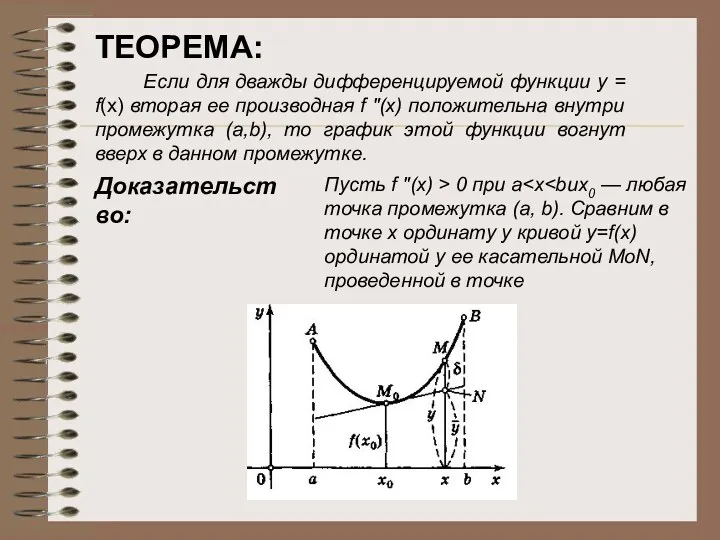
- 25. График дифференцируемой функции у = f(х) называется вогнутым вверх (или выпуклым вниз) в промежутке (а, b),
- 26. Если для дважды дифференцируемой функции y = f(х) вторая ее производная f "(х) положительна внутри промежутка
- 28. Скачать презентацию




















 Статистичні показники
Статистичні показники Геометрические фигуры. Знакомимся.
Геометрические фигуры. Знакомимся. Золотой прямоугольник. Спираль и золотое сечение
Золотой прямоугольник. Спираль и золотое сечение Обобщающий урок по теме Обыкновенные дроби 4 класс
Обобщающий урок по теме Обыкновенные дроби 4 класс Случаи вычитания 16 -
Случаи вычитания 16 - Объемы тел. Объем прямоугольного параллелепипеда
Объемы тел. Объем прямоугольного параллелепипеда Правила дифференцирования. Производная функции
Правила дифференцирования. Производная функции Координатная плоскость и знаки зодиака
Координатная плоскость и знаки зодиака Центральный и вписанные углы
Центральный и вписанные углы Логарифмы в природе
Логарифмы в природе Дисциплина ЛААГ (линейная алгебра и аналитическая геометрия)
Дисциплина ЛААГ (линейная алгебра и аналитическая геометрия) Презентация к уроку математики 4 класс УМК Школа России М.И. Морро, М.А. Бантова
Презентация к уроку математики 4 класс УМК Школа России М.И. Морро, М.А. Бантова Формулы сокращённого умножения. Урок обобщения знаний
Формулы сокращённого умножения. Урок обобщения знаний Логические упражнения
Логические упражнения Описание свойств функции по графику. 8 класс
Описание свойств функции по графику. 8 класс Координаты вектора
Координаты вектора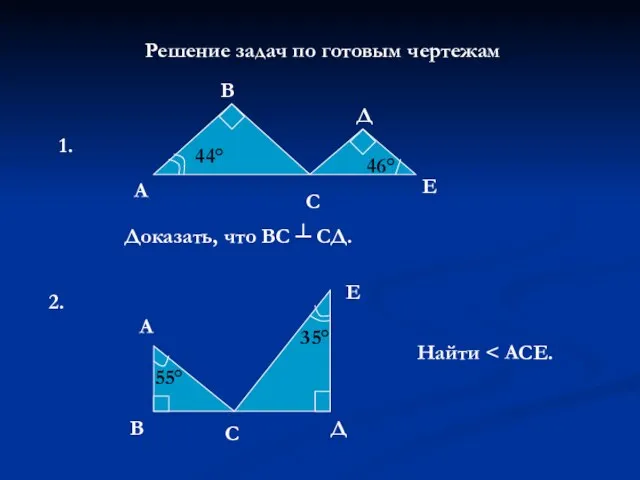 Прямоугольные треугольники. Решение задач по готовым чертежам
Прямоугольные треугольники. Решение задач по готовым чертежам Фалес Милетский. Нахождение расстояния до недоступного предмета
Фалес Милетский. Нахождение расстояния до недоступного предмета Умножение десятичных дробей
Умножение десятичных дробей Обыкновенные дроби. Урок-мозаика
Обыкновенные дроби. Урок-мозаика История возникновения чисел
История возникновения чисел Многоугольник. Выпуклый многоугольник. Четырехугольник
Многоугольник. Выпуклый многоугольник. Четырехугольник Готовимся к ОГЭ по математике, решение задания №24
Готовимся к ОГЭ по математике, решение задания №24 Презентация История цифр для 1 класса
Презентация История цифр для 1 класса Решение нестандартных уравнений
Решение нестандартных уравнений Неопределенный интеграл
Неопределенный интеграл Примеры способов определения понятий в математике в начальной школе
Примеры способов определения понятий в математике в начальной школе Решение примеров на табличное умножение и деление
Решение примеров на табличное умножение и деление