Содержание
- 2. Дадим аргументу х приращение Δх и найдем значение функции y+Δy: Находим приращение функции Используем схему нахождения
- 3. Составляем отношение Находим предел этого отношения: Сделаем замену:
- 4. Тогда В силу непрерывности логарифмической функции меняем местами знаки логарифма и предела:
- 5. производная натурального логарифма Для сложной функции:
- 6. ПРИМЕР.
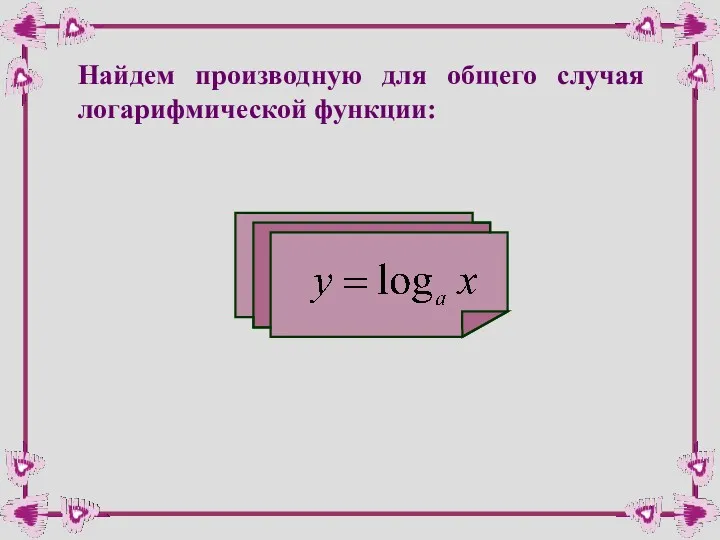
- 7. Найдем производную для общего случая логарифмической функции:
- 8. По свойству логарифма Тогда Отсюда окончательно имеем
- 9. производная логарифмической функции Для сложной функции:
- 10. ПРИМЕР.
- 11. 2. Производная показательной функции Сначала рассмотрим частный случай показательной функции:
- 12. Логарифмируем обе части равенства по основанию e: Дифференцируем обе части равенства по х: Отсюда выражаем искомую
- 13. производная экспоненты Для сложной функции:
- 14. Кривая (экспонента) обладает свойством: в каждой точке х ордината у равна угловому коэффициенту касательной к кривой
- 15. ПРИМЕР.
- 16. Найдем производную для общего случая показательной функции:
- 17. Т.к.
- 18. производная показательной функции Для сложной функции:
- 19. ПРИМЕР.
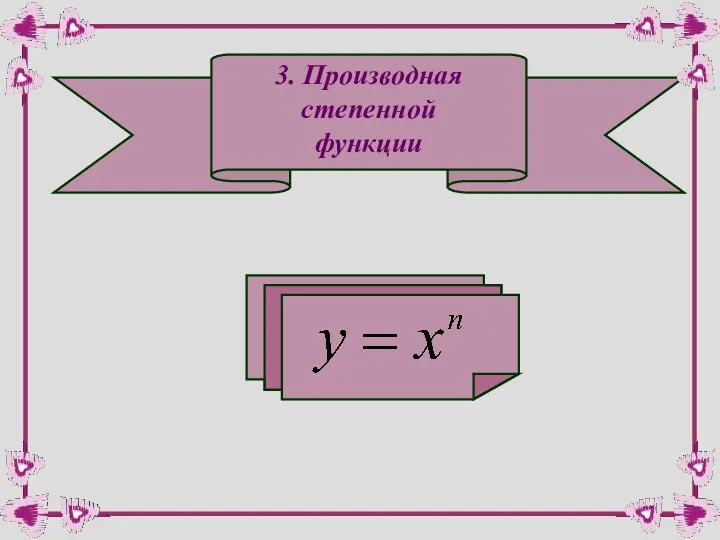
- 20. 3. Производная степенной функции
- 21. Логарифмируем обе части равенства по основанию e: Дифференцируем обе части равенства по х:
- 22. Отсюда выражаем искомую производную: Т.к. то окончательно получаем:
- 23. производная степенной функции Для сложной функции:
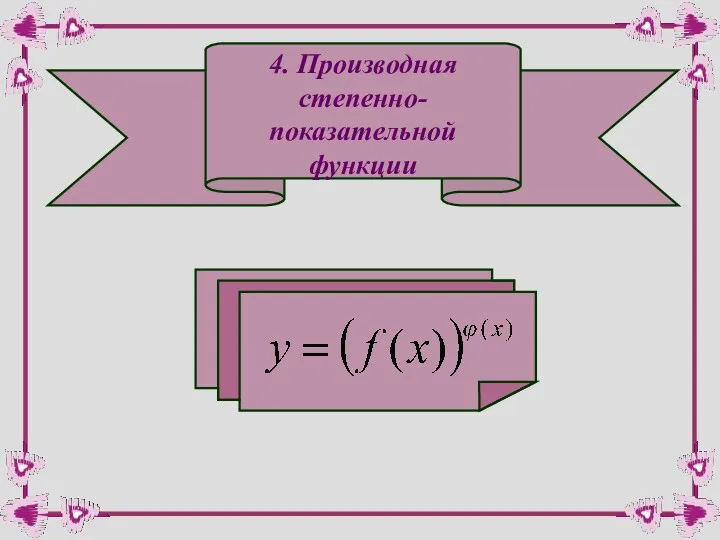
- 24. 4. Производная степенно- показательной функции
- 25. Логарифмируем обе части равенства по основанию e: Дифференцируем обе части равенства по х, учитывая, что в
- 27. Т.к. то окончательно получаем:
- 28. Чтобы продифференцировать степенно-показательную функцию, ее сначала нужно продифференцировать как показательную функцию, а затем как степенную и
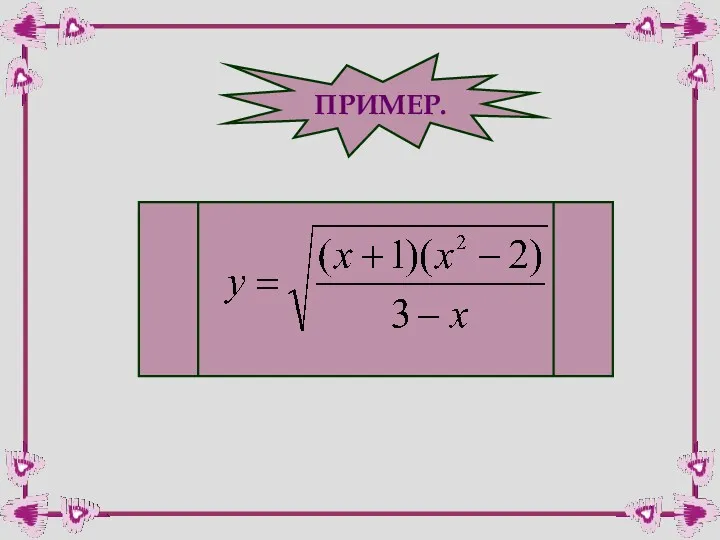
- 29. ПРИМЕР.
- 30. ЗАМЕЧАНИЕ Производная логарифмической функции называется логарифмической производной. Ее удобно использовать для дифференцирования функции, выражение которой существенно
- 31. ПРИМЕР.
- 32. Логарифмируем обе части равенства по основанию e: Используем свойства логарифма:
- 33. Дифференцируем обе части равенства по х:
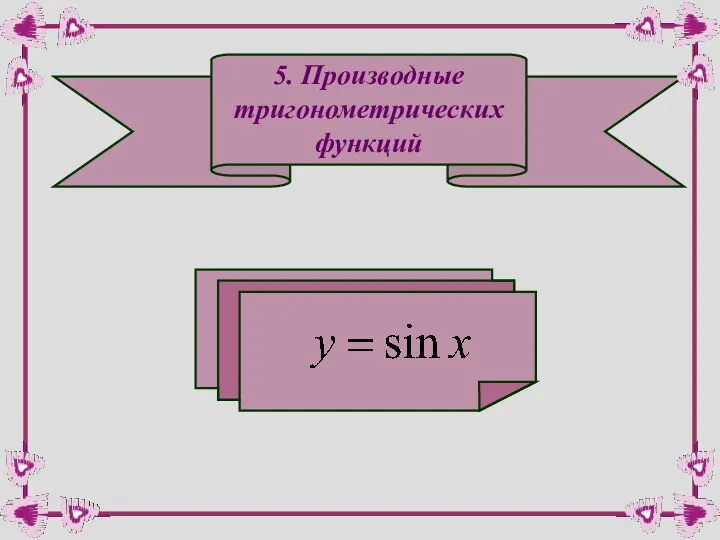
- 34. 5. Производные тригонометрических функций
- 35. Дадим аргументу х приращение Δх и найдем значение функции y+Δy: Находим приращение функции Используем схему нахождения
- 36. Составляем отношение Находим предел этого отношения:
- 37. Первый предел сводим к первому замечательному:
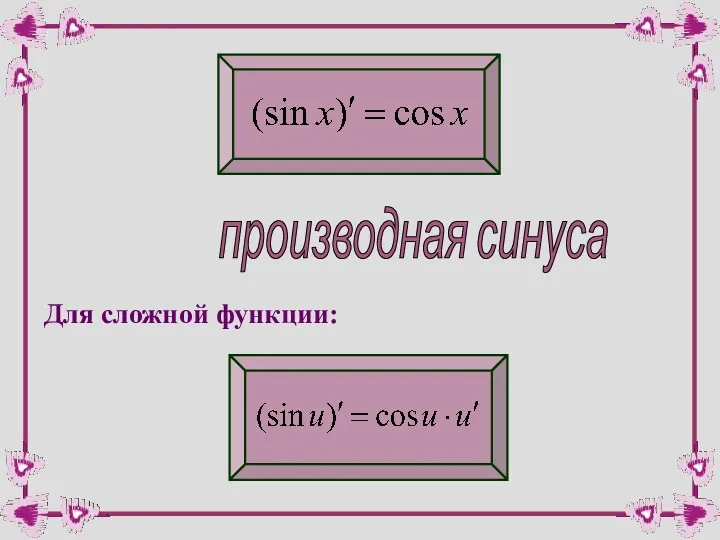
- 38. производная синуса Для сложной функции:
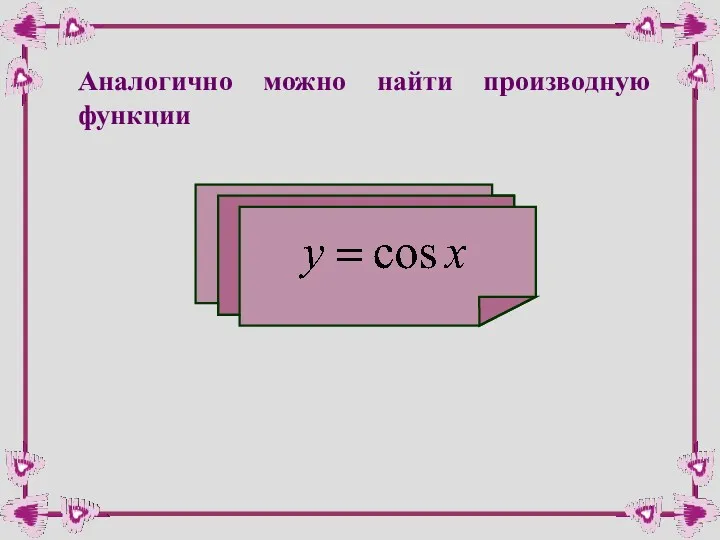
- 39. Аналогично можно найти производную функции
- 40. производная косинуса Для сложной функции:
- 41. ПРИМЕР.
- 42. Найдем производную функции
- 43. Находим производную дроби:
- 44. производная тангенса Для сложной функции:
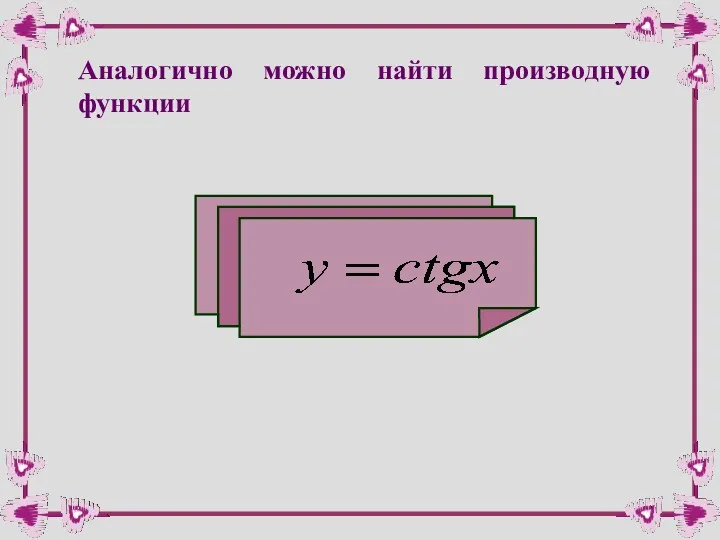
- 45. Аналогично можно найти производную функции
- 46. производная котангенса Для сложной функции:
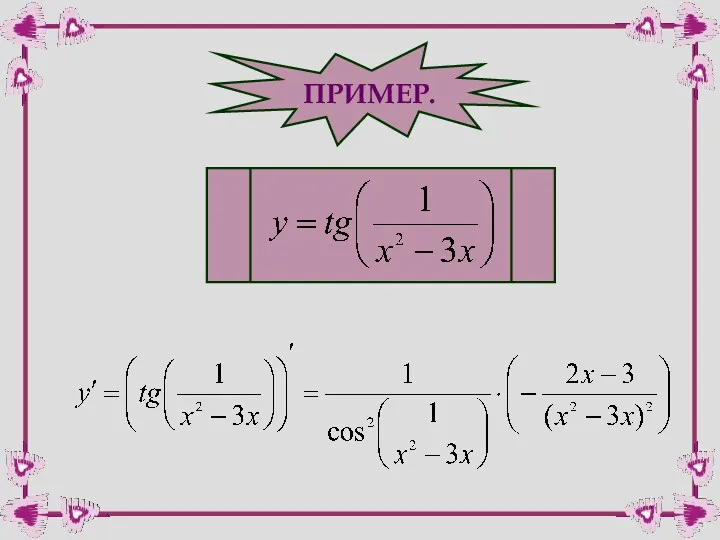
- 47. ПРИМЕР.
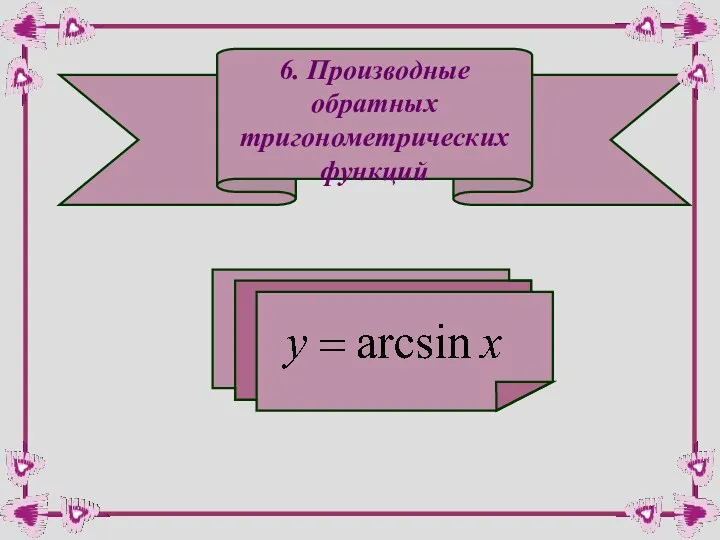
- 48. 6. Производные обратных тригонометрических функций
- 49. Обратной к ней функцией будет Используем правило дифференцирования обратной функции: Теперь нужно выразить у через х
- 50. производная арксинуса Для сложной функции:
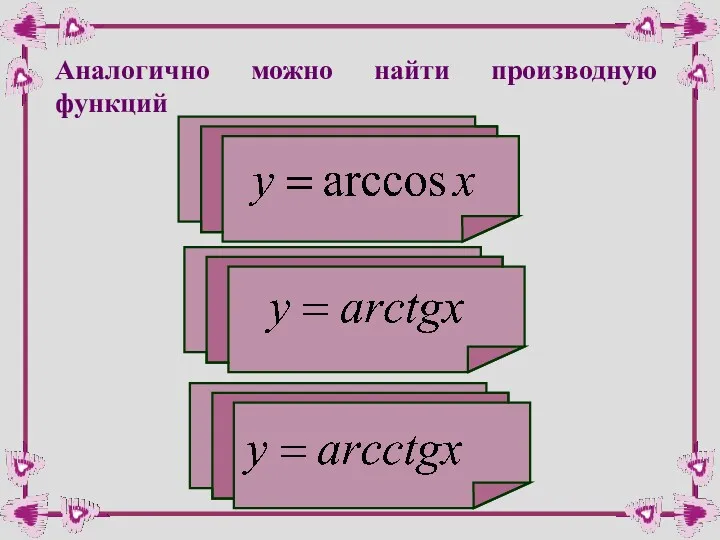
- 51. Аналогично можно найти производную функций
- 52. производная арккосинуса Для сложной функции:
- 53. производная арктангенса Для сложной функции:
- 54. производная арккотангенса Для сложной функции:
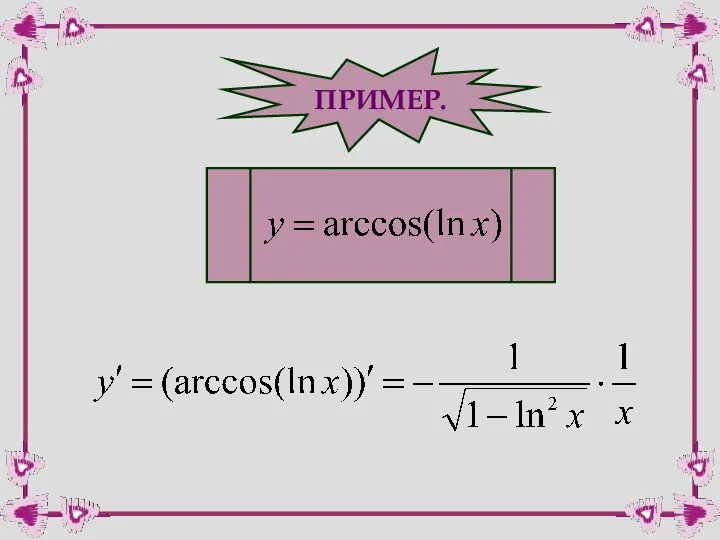
- 55. ПРИМЕР.
- 63. Скачать презентацию







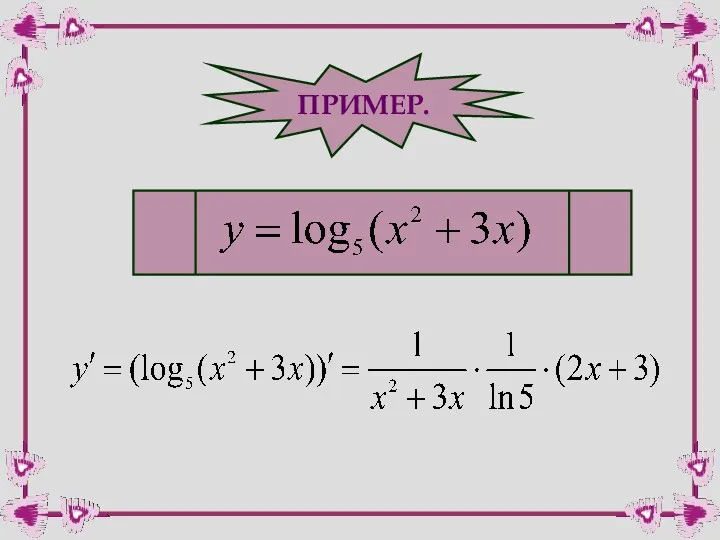






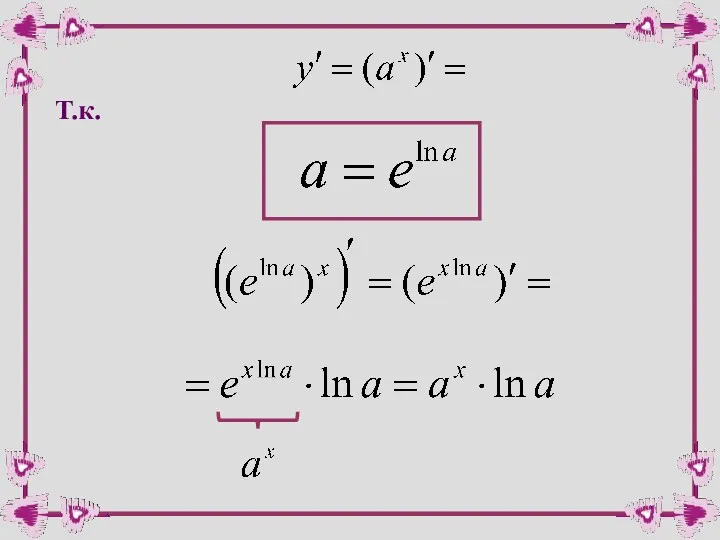






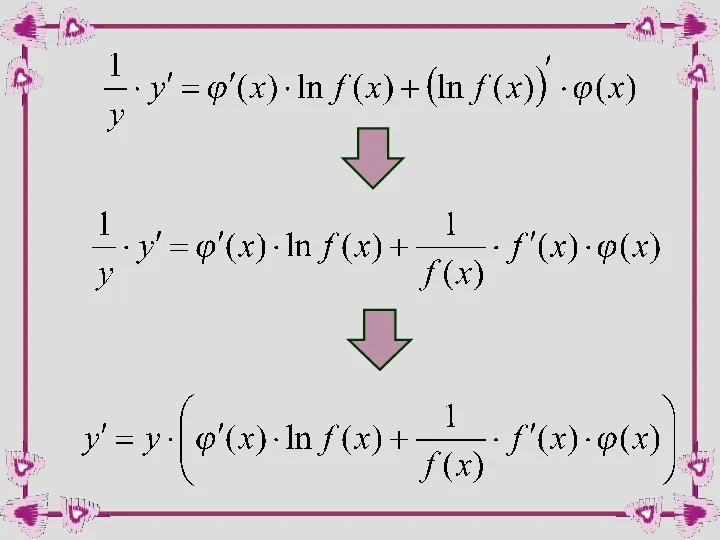










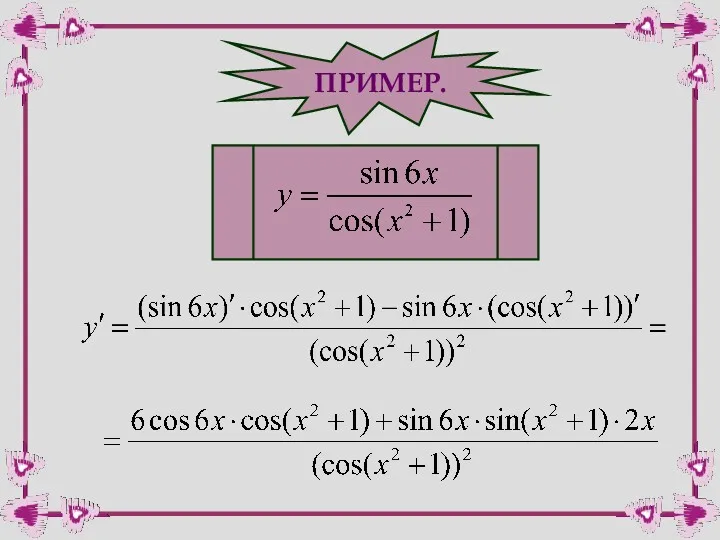















 Перпендикулярные прямые
Перпендикулярные прямые Решение задач с помощью кругов Эйлера
Решение задач с помощью кругов Эйлера Сложение - занятие на основе тетради Раз ступенька, два ступенька
Сложение - занятие на основе тетради Раз ступенька, два ступенька Презентация Буквенные выражения
Презентация Буквенные выражения Эконометрика
Эконометрика Задачи на совместное выполнение работы
Задачи на совместное выполнение работы Средства измерений и их классификация. Лекция 7
Средства измерений и их классификация. Лекция 7 Презентация: Сложение и вычитание чисел
Презентация: Сложение и вычитание чисел Критерий согласия. Практический пример применения критерия согласия. Закон Менделя
Критерий согласия. Практический пример применения критерия согласия. Закон Менделя Стохастическая модель
Стохастическая модель Нормальное распределение
Нормальное распределение Соотношения между сторонами и углами треугольника
Соотношения между сторонами и углами треугольника Игра- путешествие по математике ( 1 класс)
Игра- путешествие по математике ( 1 класс) тренажер по математике для 1 класса по теме Состав чисел первого десятка
тренажер по математике для 1 класса по теме Состав чисел первого десятка Презентация к уроку математики Космическое путешествие
Презентация к уроку математики Космическое путешествие Властивості рівнобедреного трикутника
Властивості рівнобедреного трикутника Функции и их свойства
Функции и их свойства Понятие производной. Дифференциал функции. Использование дифференциала в приближенных вычислениях. (Лекция 1)
Понятие производной. Дифференциал функции. Использование дифференциала в приближенных вычислениях. (Лекция 1) Решение задач с помощью уравнений
Решение задач с помощью уравнений Древняя Русь. Меры длины
Древняя Русь. Меры длины Четырехугольники. 8 класс
Четырехугольники. 8 класс Презентация Математическая викторина
Презентация Математическая викторина Область определения функции
Область определения функции Подготовка учащихся к ОГЭ по математике
Подготовка учащихся к ОГЭ по математике Тренажёр по математике (2 класс)
Тренажёр по математике (2 класс) Комбинаторика
Комбинаторика Урок-путешествие в страну отрицательных чисел для 6 класса
Урок-путешествие в страну отрицательных чисел для 6 класса Повторение по теме Величины
Повторение по теме Величины