Содержание
- 2. Производной n –го порядка называется производная от производной n-1 –го порядка. Обозначается: - производная второго порядка
- 3. Выясним механический смысл второй производной. Если точка движется прямолинейно по закону S=S(t), то - есть скорость
- 4. ПРИМЕР. Найти вторую производную функции
- 6. ОСНОВНЫЕ ТЕОРЕМЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ Рассмотрим три важнейшие теоремы дифференциального исчисления: теорему Ферма, теорему Ролля и теорему
- 7. Теорема Ферма Если дифференцируемая на промежутке Х функция y=f(x) достигает наибольшего или наименьшего значения во внутренней
- 8. Доказательство: Пусть функция y=f(x) дифференцируема на промежутке Х и в точке принимает наименьшее значение. Тогда если
- 9. Величина Следовательно при при
- 10. и По условию функция y=f(x) дифференцируема в точке х0, следовательно ее предел при Переходим в этих
- 11. Геометрический смысл теоремы Ферма В точке наибольшего или наименьшего значения, достигаемого внутри промежутка Х, касательная к
- 13. Теорема Ролля Пусть функция y=f(x) удовлетворяет следующим условиям: Непрерывна на отрезке [a,b]. Дифференцируема на интервале (a,b).
- 14. Тогда внутри отрезка существует по крайней мере одна такая точка ξ, в которой производная функции равна
- 15. Доказательство: На основании теоремы Вейерштрасса, функция, непрерывная на отрезке, достигает на нем своего наибольшего М и
- 16. Если же хотя бы одно из этих значений (минимальное или максимальное), достигается внутри отрезка, то по
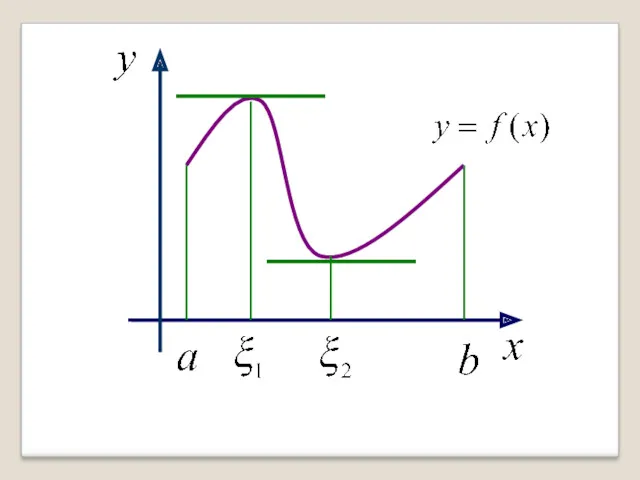
- 17. Геометрический смысл теоремы Ролля Найдется хотя бы одна точка, в которой касательная к графику функции параллельна
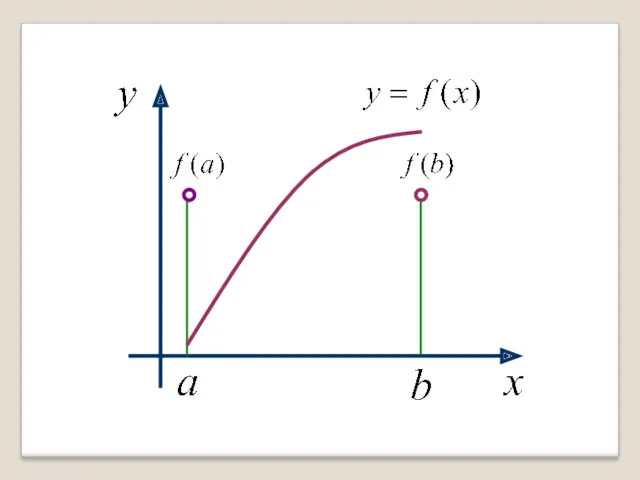
- 19. Если же хотя бы одно условие теоремы Ролля нарушено, то заключение теоремы может быть неверным. Например:
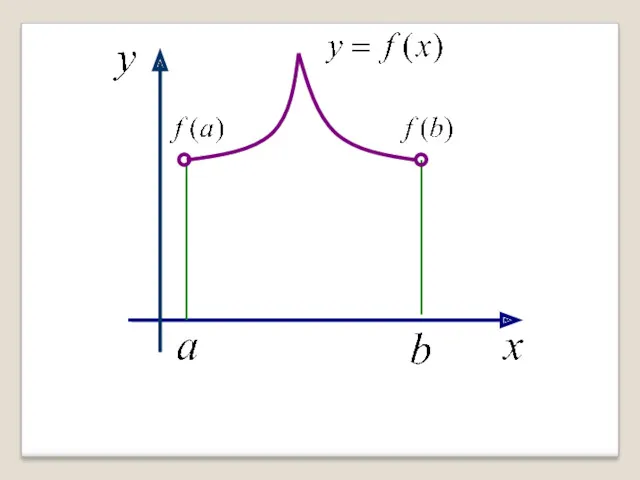
- 21. Отсутствует дифференцируемость на (a,b). 2
- 23. 3
- 25. Теорема Лагранжа Пусть функция y=f(x) удовлетворяет следующим условиям: Непрерывна на отрезке [a,b]. Дифференцируема на интервале (a,b).
- 26. Тогда внутри отрезка существует по крайней мере одна такая точка ξ, в которой производная функции равна
- 27. Доказательство: Введем новую функцию g(x): Эта функция удовлетворяет всем условиям теоремы Ролля: Она непрерывна на [a,b],
- 29. Следовательно, по теореме Ролля существует точка такая, что или
- 30. отсюда
- 31. Эту теорему часто записывают в виде:
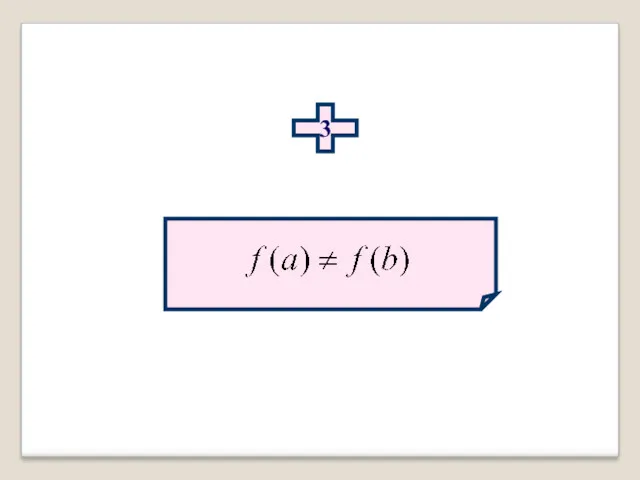
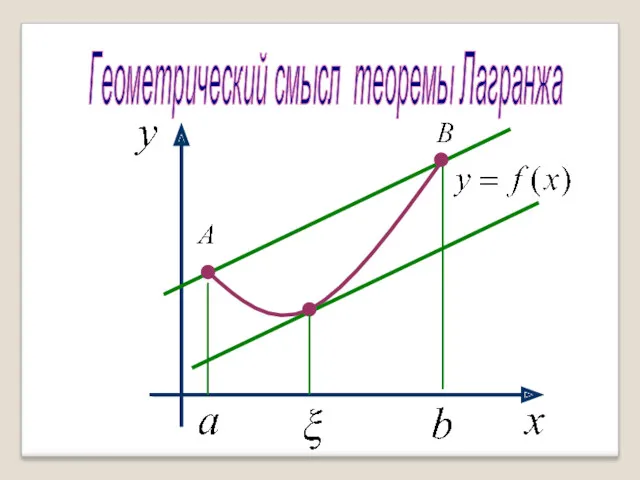
- 32. Геометрический смысл теоремы Лагранжа
- 33. Если перемещать прямую АВ параллельно начальному положению, то найдется хотя бы одна точка в которой касательная
- 34. Следствие Если производная функции y=f(x) равна 0 на некотором промежутке Х, то эта функция постоянна на
- 35. Доказательство: Возьмем на промежутке Х [a,х], тогда по теореме Лагранжа По условию теоремы
- 37. Скачать презентацию



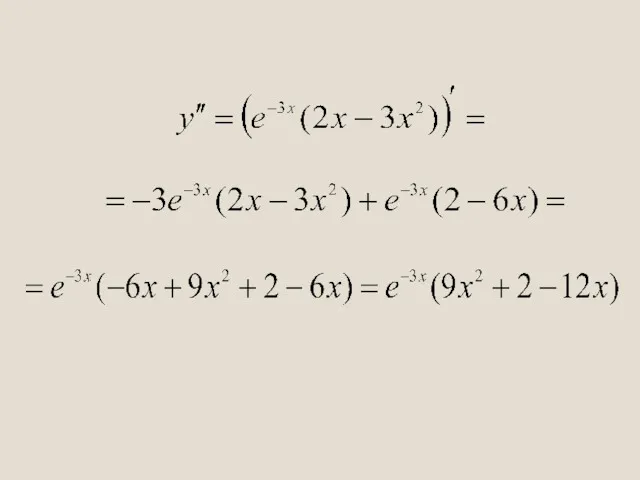















![Теорема Лагранжа Пусть функция y=f(x) удовлетворяет следующим условиям: Непрерывна на отрезке [a,b]. Дифференцируема на интервале (a,b).](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/139347/slide-24.jpg)








![Доказательство: Возьмем на промежутке Х [a,х], тогда по теореме Лагранжа По условию теоремы](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/139347/slide-34.jpg)
 ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ многочленом Ньютона
ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ многочленом Ньютона Урок - путешествие (презентация) 3 класс, математика, автор М. И. Моро
Урок - путешествие (презентация) 3 класс, математика, автор М. И. Моро Прямоугольные треугольники и некоторые их свойства
Прямоугольные треугольники и некоторые их свойства Название компонентов и результата действия деления. 2 класс
Название компонентов и результата действия деления. 2 класс Счет в пределах 10, 1 класс Зимняя сказка
Счет в пределах 10, 1 класс Зимняя сказка Шаблоны презентаций по математике
Шаблоны презентаций по математике Сложение и вычитание трехзначных чисел
Сложение и вычитание трехзначных чисел Презентация к уроку математики в форме игры Биржа
Презентация к уроку математики в форме игры Биржа Урок математики. Многозначные числа и действия с ними.
Урок математики. Многозначные числа и действия с ними. Обобщающий урок по теме Четырехугольники
Обобщающий урок по теме Четырехугольники урок математики с презентацией
урок математики с презентацией Старинные измерения величин
Старинные измерения величин Презентация к уроку математики 2 класс
Презентация к уроку математики 2 класс Неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. (Лекция 2.11)
Неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. (Лекция 2.11) Решение задач. Коллекция задач для 6 класса по математике
Решение задач. Коллекция задач для 6 класса по математике Случайные величины
Случайные величины Презентация к уроку математики 1 класс Занков Диск
Презентация к уроку математики 1 класс Занков Диск Урок Сложение двузначных чисел в столбик, технология проблемного обучения
Урок Сложение двузначных чисел в столбик, технология проблемного обучения Экстремумы функции
Экстремумы функции Сложение и вычитание чисел в пределах 100
Сложение и вычитание чисел в пределах 100 Логарифмическая функция, её свойства и график
Логарифмическая функция, её свойства и график Маса. Кілограм (урок № 64)
Маса. Кілограм (урок № 64) Проценты
Проценты Проверка деления умножением
Проверка деления умножением Прямая и отрезок
Прямая и отрезок открытый урок по математике 4 класс
открытый урок по математике 4 класс Соотношения между сторонами и углами прямоугольного треугольника
Соотношения между сторонами и углами прямоугольного треугольника Прямая и обратная пропорциональные зависимости
Прямая и обратная пропорциональные зависимости