Содержание
- 2. Конечные разности Пусть функция задана таблицей с постоянным шагом. Разности между значениями функции в соседних узлах
- 3. Продолжая этот процесс, можно по заданной таблице функции составить таблицу конечных разностей. Конечные разности любого порядка
- 4. Методом математической индукции можно доказать, что
- 5. Первая интерполяционная формула Ньютона Пусть для функции, заданной таблицей с постоянным шагом, составлена таблица конечных разностей.
- 6. Полагая х = х0, находим у0 = Pn(x0) = а0, откуда а0 = у0. Далее, придавая
- 7. Подставим теперь найденные значения ak в выражение для многочлена: Практически эта формула применяется в несколько ином
- 8. Окончательно имеем: Эта формула называется первой интерполяци-онной формулой Ньютона и применяется для интерполирования в начале отрезка
- 9. Вторая интерполяционная формула Ньютона Когда значение аргумента находится ближе к концу отрезка интерполяции, применять первую интерполяционную
- 10. Как и для первой формулы Ньютона, коэффициенты a0, a1, an находятся из условия совпадения значений функции
- 11. Получим окончательный вид второй интерполяционной формулы Ньютона:
- 12. Оценка погрешности интерполяционных формул Ньютона
- 13. Пример Построить интерполяционный многочлен Ньютона для функции, заданной таблично: Построим таблицу конечных разностей: h=2
- 15. Скачать презентацию












 Порівняння раціональних чисел. Математика. 6 клас
Порівняння раціональних чисел. Математика. 6 клас Угол между скрещивающимися прямыми
Угол между скрещивающимися прямыми Урок математики Решение задач
Урок математики Решение задач урок математики
урок математики Точечные перфокарты.
Точечные перфокарты. Итоговый тест по математике
Итоговый тест по математике Числовые последовательности
Числовые последовательности Уравнение окружности (9 класс)
Уравнение окружности (9 класс) Практическое применение знаний по математике, связанных с сельским хозяйством
Практическое применение знаний по математике, связанных с сельским хозяйством Урок математики в 1 классе на тему Приёмы сложения и вычитания, основанные на знании нумерации чисел
Урок математики в 1 классе на тему Приёмы сложения и вычитания, основанные на знании нумерации чисел Круглые числа. Состав числа 9. Сравнение выражений
Круглые числа. Состав числа 9. Сравнение выражений Урок Числа от 10 до 20
Урок Числа от 10 до 20 Вычитание чисел (часть 1)
Вычитание чисел (часть 1) Применение признаков равенства треугольников при решении задач
Применение признаков равенства треугольников при решении задач Метод максимального правдоподобия
Метод максимального правдоподобия Формирование УУД на различных этапах урока математики по ТДМ.
Формирование УУД на различных этапах урока математики по ТДМ. Преобразование графиков тригонометрических функций
Преобразование графиков тригонометрических функций Дифференциальные уравнения и их применение в медицинской практике
Дифференциальные уравнения и их применение в медицинской практике Второй признак равенства треугольников
Второй признак равенства треугольников Элементы матанализа. Применение производной при исследовании функции
Элементы матанализа. Применение производной при исследовании функции Таблица деления на 3
Таблица деления на 3 Функция её свойства и график
Функция её свойства и график Ряды динамики. Статистика
Ряды динамики. Статистика Vienkāršās formas
Vienkāršās formas Математический КВН
Математический КВН Вписані і центральні кути
Вписані і центральні кути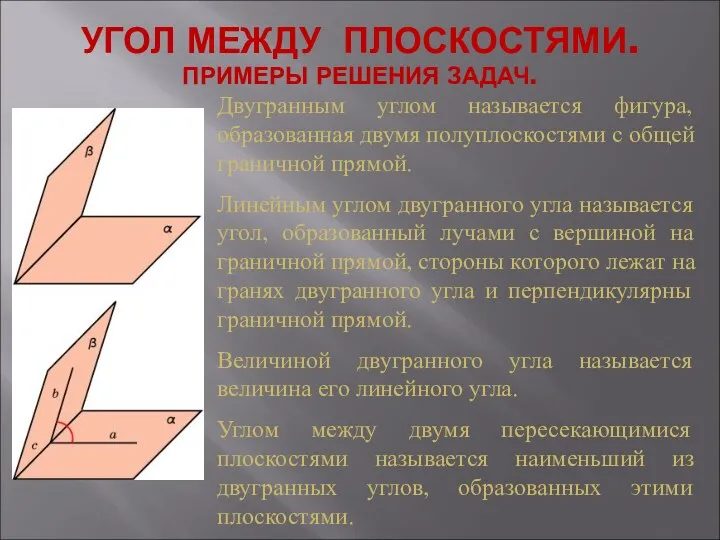 Угол между плоскостями. Примеры решения задач
Угол между плоскостями. Примеры решения задач Высота и скорость полета. (Тема 6)
Высота и скорость полета. (Тема 6)