Прямая и плоскость в пространстве. (Лекция 6) презентация

Уравнение плоскости по заданным точке и нормальному вектору.
Mo(xо, yо, zо) – заданная точка, лежащая в плоскости Q.
– нормальный вектор плоскости.

Общее уравнение плоскости.
Любой плоскости соответствует уравнение первой степени (линейное) относительно текущих декартовых координат.
Верно и обратное: любому уравнению первой степени относительно переменных x, y и z соответствует некоторая плоскость.

Взаимное расположение двух плоскостей. Угол между плоскостями.

Условия параллельности и перпендикулярности двух плоскостей.
Две плоскости параллельны тогда и только тогда, когда коллинеарны их нормальные векторы.
Для параллельности двух плоскостей необходимо и достаточно, чтобы коэффициенты при соответствующих текущих координатах были пропорциональны:
Две плоскости перпендикулярны тогда и только тогда, когда ортогональны их нормальные векторы.
Для перпендикулярности двух плоскостей необходимо и достаточно, чтобы сумма произведений коэффициентов при одноименных текущих координатах равнялась нулю:

Прямая в пространстве.
Линию в пространстве, в том числе и прямую, можно рассматривать как пересечение двух поверхностей.
Любая линия в пространстве определяется как геометрическое место точек, координаты которых одновременно удовлетворяют уравнению каждой поверхности.

Прямая в пространстве.
Широкое применение, особенно в теоретической механике, физике и других дисциплинах, находит параметрическое задание линии, при котором текущие декартовы координаты задаются как некоторые функции параметра t , который обычно трактуют как время. Уравнения линии в этом случае называют законом движения точки, а саму линию - траекторией движения.

Прямая как пересечение плоскостей.
Рассмотрим две плоскости Q1 и Q2 , заданные уравнениями
Если в уравнениях системы данной системы коэффициенты при текущих координатах не пропорциональны, то есть плоскости не параллельны, то эта система определяет прямую L как пересечение плоскостей Q1 и Q2.

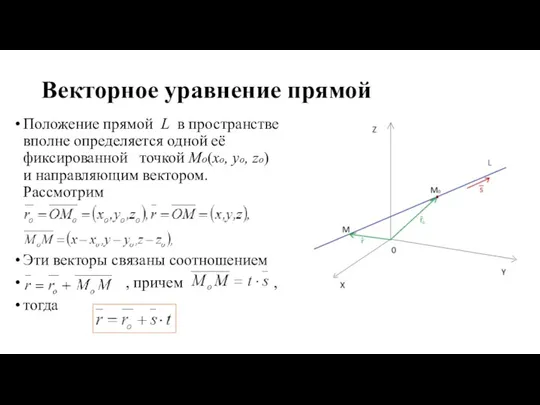
Векторное уравнение прямой
Положение прямой L в пространстве вполне определяется одной её фиксированной точкой Mo(xо, yо, zо) и направляющим вектором. Рассмотрим
Эти векторы связаны соотношением
, причем ,
тогда

Параметрические уравнения прямой в пространстве.

Канонические уравнения прямой в пространстве.

Уравнение прямой по двум заданным точкам.
Пусть прямая проходит через две заданные точки M1(x1, y1, z1) и M2(x2, y2, z2) . Запишем каноническое уравнение прямой, взяв в качестве направляющего вектор
Тогда уравнение прямой по двум заданным точкам:

Угол между прямыми в пространстве.
Рассмотрим две прямые L1 и L2 , для которых известны их канонические уравнения, тогда один из двух смежных углов, образованных прямыми, равен углу между их направляющими векторами, поэтому

Условия параллельности и перпендикулярности двух прямых в пространстве.
Условия параллельности и перпендикулярности прямых равносильны соответствующим условиям для направляющих векторов:

Угол между прямой и плоскостью.
Углом ϕ между прямой и плоскостью называется угол между прямой и её проекцией на эту плоскость.
Рассмотрим прямую L и плоскость Q , заданные уравнениями:
Тогда синус угла между ними: