Содержание
- 2. Линейная регрессия Множественная линейная регрессия
- 3. Регрессионный анализ – количественное представление связи или зависимости между зависимой переменной (откликом) и независимой / независимыми
- 5. Эстонский исследователь Я. Микк, изучая трудности понимания текста, установил «формулу читаемости», которая представляет собой множественную линейную
- 6. Линейную регрессию можно отразить уравнением прямой линии: Y = b1 · X + с, где: Y
- 7. Пример: зависимость агрессивности у спортсменов от фрустрации
- 8. H – это коэффициент корреляции между зависимой и независимой переменными (r = 0,418), R-квадрат - коэффициент
- 9. Y = b1 · X + с, b1 – нестандартизированный коэффициент В, с – константа ⇒
- 10. Общее назначение множественной регрессии (Pearson, 1908) - анализ связи между несколькими независимыми переменными (регрессорами или предикторами)
- 11. При расчетах оценок параметров регрессионной модели применяется метод наименьших квадратов. В условиях нормального распределения ошибок оценки
- 12. Пример: зависимость агрессивности у спортсменов от фрустрации и тревожности «Агрессивность» = b1 ·«Фрустрация» + b2 ·
- 13. H – коэффициент множественной корреляции между зависимой и набором независимых переменных (0,464), а R-квадрат - коэффициент
- 14. Multiple R – коэффициент множественной корреляции. Может принимать значения от 0 до 1 и характеризует тесноту
- 15. Коэффициент детерминации R² измеряет долю разброса относительно среднего значения, которую «объясняет» построенная регрессия. Значение R² является
- 16. Значение критерия F-Фишера равно 12,735, его p-уровень значимости – 0,000. Это означает, что коэффициент множественной корреляции
- 17. В таблице – стандартизированные коэффициенты регрессии (Бета) – 0,276 и 0,229, значения критерия t-Стьюдента (2,195 и
- 18. Бета-коэффициенты β - это коэффициенты, которые получатся, если предварительно стандартизовать все переменные к среднему 0 и
- 20. Частная корреляция Частная корреляция - анализ взаимосвязи между двумя величинами при фиксированных значениях остальных величин. Частная
- 21. Пример: у группы спортсменов измерили результат в прыжках в длину (Х), массу тела (Y) и силу
- 22. Представим, что исследователя интересует "чистая" корреляция между результатами в прыжках в длину и массой тела, исключая
- 23. Summary Statistics; DV: NEP (ЭкПс-2016-17-для МногомАнализ.sta) Regression Summary for Dependent Variable: NEP (ЭкПс-2016-17-для МногомАнализ.sta) R= ,60908975
- 24. Variables currently in the Equation; DV: NEP (ЭкПс-2016-17-для МногомАнализ.sta)
- 25. Формула счастья котиков Очевидно, что каждый подранный диван делает котиков гораздо счастливее, чем очередное увеличение пайков.
- 26. Коэффициент b1 определяется как тангенс угла между линией котиков и оси x. Чем больше этот коэффициент,
- 28. Реальные взаимосвязи мало похожи на прямую линию. Чаще они напоминают собой огурец, а в запущенных случаях
- 31. Предположения, ограничения и обсуждение практических вопросов www.statsoft.ru/home/textbook/modules/stmulreg.html Предположение линейности. Предполагается, что связь между переменными является линейной.
- 32. Предположение нормальности. В множественной регрессии предполагается, что остатки (предсказанные значения минус наблюдаемые) распределены нормально (т.е. подчиняются
- 33. Ограничения. Основное концептуальное ограничение всех методов регрессионного анализа состоит в том, что они позволяют обнаружить только
- 34. Выбор числа переменных. Множественная регрессия предоставляет пользователю "соблазн" включить в качестве предикторов все переменные, какие только
- 35. Принцип здравого смысла: регрессор должен иметь логические взаимоотношения с зависимой переменной, кроме статистических взаимоотношений
- 36. Наилучшие регрессионные модели Поиск наилучшей регрессионной модели – искусство, у которого нет рецептов. С одной стороны,
- 38. Скачать презентацию



































 Координатная проскость. Прямоугольная (декартова) система координат
Координатная проскость. Прямоугольная (декартова) система координат Презентация по математике Измеряем длину
Презентация по математике Измеряем длину Чтение графиков, диаграмм, таблиц
Чтение графиков, диаграмм, таблиц Вартість. Гривня і копійка. Дії з іменованими числами. Урок №101
Вартість. Гривня і копійка. Дії з іменованими числами. Урок №101 Математика. 1 класс. Урок 78. Величины. Масса. Килограмм - Презентация
Математика. 1 класс. Урок 78. Величины. Масса. Килограмм - Презентация Простейшие задачи в координатах
Простейшие задачи в координатах Понятие производной
Понятие производной открытое занятие по ФЭМП во второй младшей группе
открытое занятие по ФЭМП во второй младшей группе Меры центральной тенденции. Лекция 03
Меры центральной тенденции. Лекция 03 Величины и их измерение
Величины и их измерение Математическая логика и теория алгоритмов
Математическая логика и теория алгоритмов Случайные события и их вероятность
Случайные события и их вероятность Решение задач на проценты. Как найти % от числа
Решение задач на проценты. Как найти % от числа Случаи вычитания 17 -, 18 -
Случаи вычитания 17 -, 18 - Введение в эконометрику
Введение в эконометрику Метод построения таблиц сопряженности
Метод построения таблиц сопряженности Представление дробей на координатном луче
Представление дробей на координатном луче Преобразование алгебраических выражений
Преобразование алгебраических выражений Путешествие в страну Математики
Путешествие в страну Математики Сравнение дробей с одинаковыми знаменателями. 5 класс
Сравнение дробей с одинаковыми знаменателями. 5 класс Сумма и разность синусов и косинусов
Сумма и разность синусов и косинусов Решение задач линейного программирования графическим методом
Решение задач линейного программирования графическим методом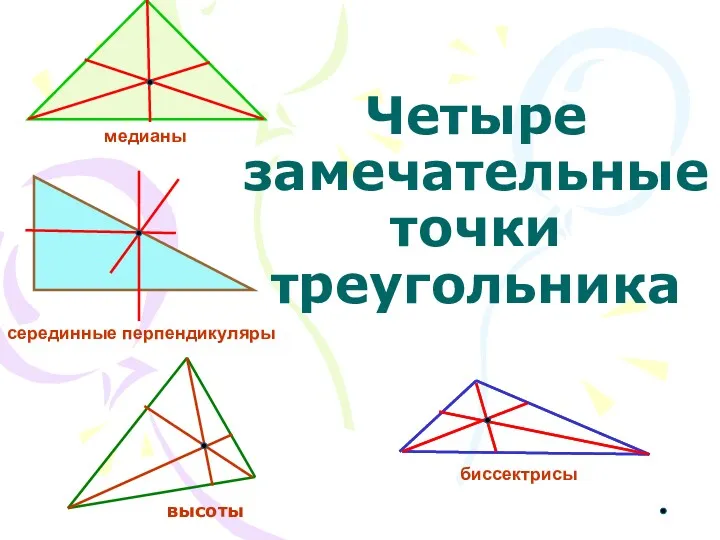 Четыре замечательные точки треугольника
Четыре замечательные точки треугольника Тест по теме Объем пирамиды
Тест по теме Объем пирамиды Презентация по теме Виды треугольников
Презентация по теме Виды треугольников Бинарные отношения
Бинарные отношения Математические диктанты
Математические диктанты Умножение десятичных дробей на 10, 100 1000 и.т.д
Умножение десятичных дробей на 10, 100 1000 и.т.д