Содержание
- 2. Основные обозначения: система линейных алгебраических уравнений (СЛАУ): матричная запись СЛАУ: А⋅ Х=В , где
- 4. расширенная матрица системы: однородная СЛАУ:
- 5. Методы решения СЛАУ: правило Крамера; матричный метод; (рассматриваться в данной работе не будет) метод Гаусса
- 6. Правило Крамера Решает системы n – линейных алгебраических уравнений с n – неизвестными общего вида причем
- 7. Определение. Определитель, составленный из коэффициентов при неизвестных системы называется главным определителем системы, обозначается ∆:
- 8. Правило Крамера Вспомогательный определитель ∆i получается из определителя ∆ путем замены соответствующего i-го столбца столбцом свободных
- 9. Теорема (правило Крамера) Если главный определитель ∆ системы размерности n×n отличен от нуля, то система имеет
- 10. Рассмотрим систему n линейных уравнений c n неизвестными: Теорема Крамера: Пусть Δ - определитель матрицы системы,
- 11. Определитель квадратной матрицы – это число, вычисляемое по определённым правилам. Обозначают: |А|, ΔА, detA . Вспомним
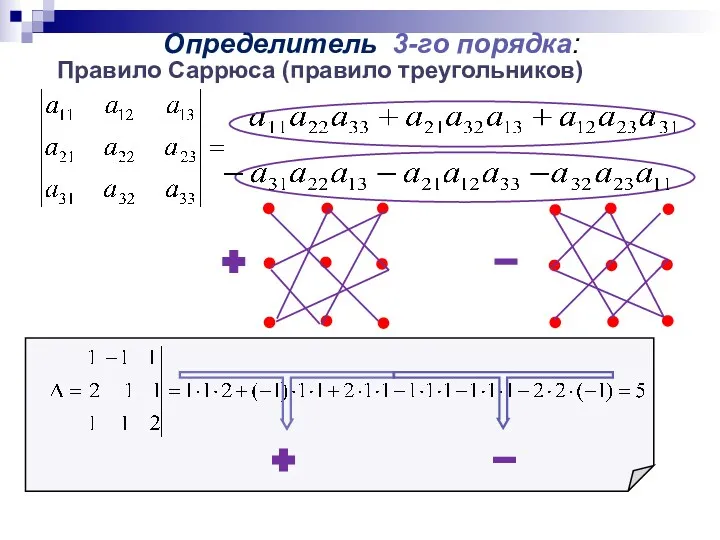
- 12. Определитель 3-го порядка: Правило Саррюса (правило треугольников)
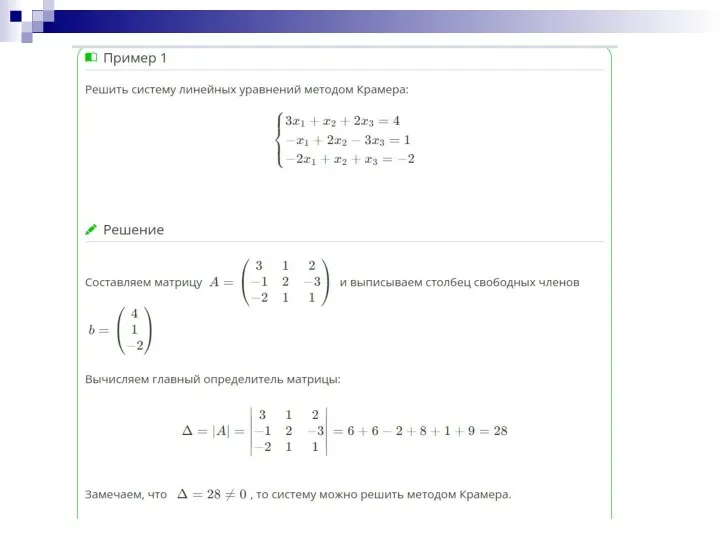
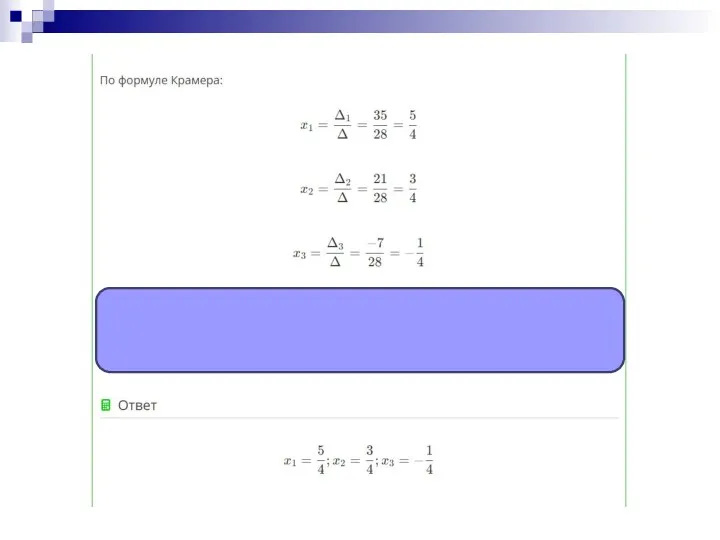
- 14. Рассмотрим сам алгоритм метода Крамера на конкретном примере
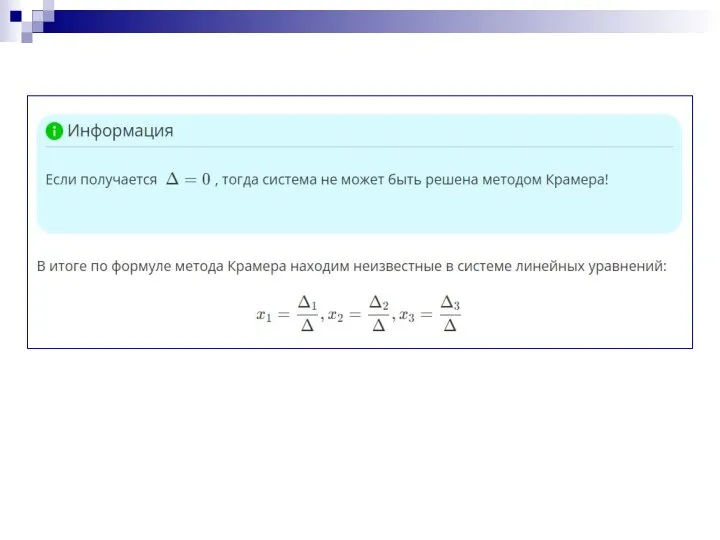
- 15. Если получается Δ=0, тогда система не может быть решена методом Крамера!
- 21. Ответ: метод Крамера нельзя применить к данной системе линейных уравнений
- 22. Пример. Решить систему методом Крамера: 3) Подставим полученные значения в формулу Крамера: Решение. 1)Определитель матрицы системы:
- 23. Метод Гаусса решения СЛАУ
- 25. Метод Гаусса Метод Гаусса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного
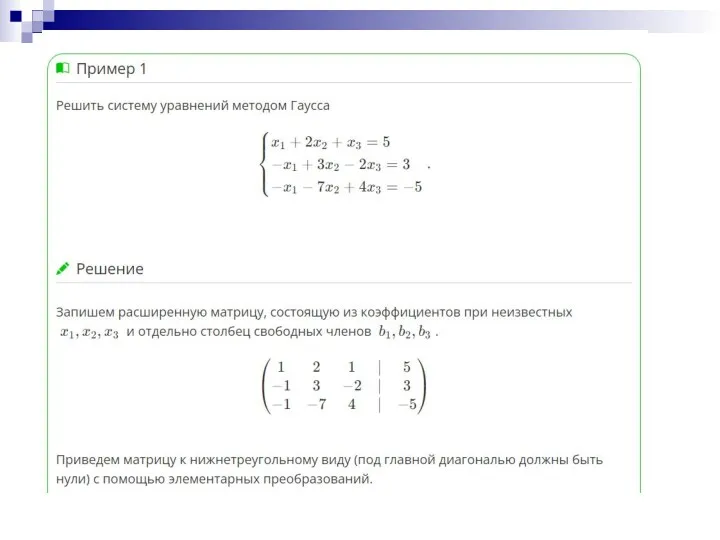
- 26. Чтобы решить систему m – линейных алгебраических уравнений с n – неизвестными методом Гаусса, необходимо записать
- 27. Элементарные преобразования расширенной матрицы системы : перестановка строк (столбцов) матрицы; умножение строки матрицы на действительное число
- 28. Рассмотри пример решения СЛАУ методом Гаусса
- 33. 2
- 37. Скачать презентацию




























 Решение неравенств второй степени с одной переменной
Решение неравенств второй степени с одной переменной Метод координат
Метод координат Математика 4 класс. Тест
Математика 4 класс. Тест Умножаем и делим на 10. 2 класс
Умножаем и делим на 10. 2 класс Показательная функция
Показательная функция Решение задач на готовых чертежах. Теорема Пифагора
Решение задач на готовых чертежах. Теорема Пифагора Понятие одночлена. Стандартный вид одночлена
Понятие одночлена. Стандартный вид одночлена Свойства прямой и обратной функций
Свойства прямой и обратной функций Трансцедентные числа π и е
Трансцедентные числа π и е Деление с остатком
Деление с остатком урок по программе Школа России 4 класс. Задачи на движение. Закрепление
урок по программе Школа России 4 класс. Задачи на движение. Закрепление Параллельность прямых и плоскостей
Параллельность прямых и плоскостей Формальные логические теории. Исчисление предикатов
Формальные логические теории. Исчисление предикатов Нахождение целого по его части на основе формального правила
Нахождение целого по его части на основе формального правила Подобные треугольников. Признаки подобия треугольников. 8 класс
Подобные треугольников. Признаки подобия треугольников. 8 класс Дії з двоцифровими числами. Творча робота над задачею. Урок №128
Дії з двоцифровими числами. Творча робота над задачею. Урок №128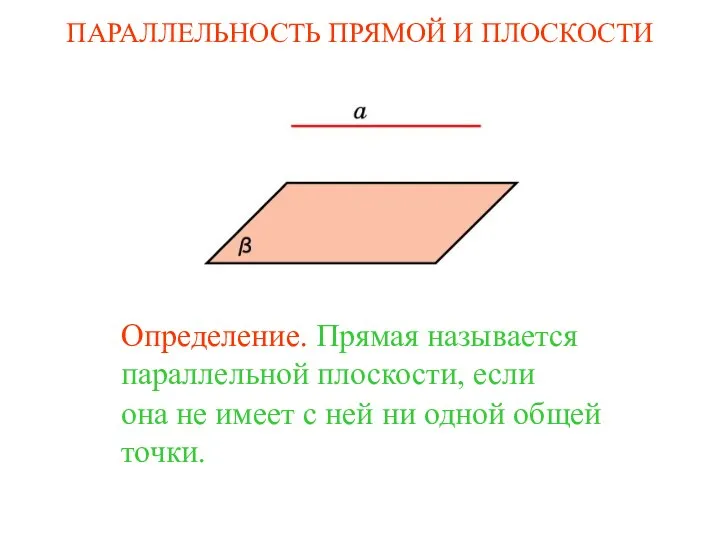 Параллельность прямой и плоскости
Параллельность прямой и плоскости Начальные сведения из стереометрии
Начальные сведения из стереометрии Прибавить и вычесть число 5.
Прибавить и вычесть число 5. Сумма n-первых членов арифметической прогрессии
Сумма n-первых членов арифметической прогрессии Решение систем уравнений способом сложения
Решение систем уравнений способом сложения Начертательная геометрия. Способы преобразования проекций. (Лекция 3)
Начертательная геометрия. Способы преобразования проекций. (Лекция 3) Движение. Виды движения
Движение. Виды движения Презентация к уроку математики во 2 классе по теме Приёмы вычислений для случаев вида 36 + 2, 36 + 20
Презентация к уроку математики во 2 классе по теме Приёмы вычислений для случаев вида 36 + 2, 36 + 20 Функция у=ах² , её свойства и график. 8 класс
Функция у=ах² , её свойства и график. 8 класс Великие педагоги и математики
Великие педагоги и математики ЕГЭ - 2017 по математике. Базовый уровень. Задачи на логику и смекалку
ЕГЭ - 2017 по математике. Базовый уровень. Задачи на логику и смекалку Производная показательной и логарифмической функций
Производная показательной и логарифмической функций