Содержание
- 2. Термин «комбинаторика» происходит от латинского слова «combina», что в переводе на русский означает – «сочетать», «соединять».
- 3. Комбинаторика - важный раздел математики, знание которого необходимо представителям самых разных специальностей. С комбинаторными задачами приходится
- 4. Комбинаторные соединения — это такие комбинации из каких-либо элементов. Типы соединений: Перестановки Размещения Сочетания Существуют две
- 5. ФАКТОРИАЛ ЧИСЛА Факториал числа — это произведение всех натуральных чисел до этого числа включительно. Обозначается с
- 6. Значения факториалов от 0 до 10. 0! = 1 1! = 1 2! = 1 ·
- 7. Свойство факториала: (n + 1)! = (n + 1) · n! Например: (5 + 1)! =
- 8. Задача Сколькими способами могут восемь человек стать в очередь к театральной кассе? Решение. Существует 8 мест,
- 9. ПЕРЕСТАНОВКИ Перестановки без повторений — комбинаторные соединения, которые могут отличаться друг от друга лишь порядком входящих
- 10. Задача Сколько четырёхзначных чисел можно записать с помощью цифр 1,2,3,4, если каждая цифра входит в число
- 11. Примеры Сколькими способами можно переставлять друг с другом цифры 1,2,3,4? За столом 5 мест. Сколькими способами
- 12. Перестановки с повторениями — комбинаторные соединения, в которых среди образующих элементов имеются одинаковые. В таких соединениях
- 13. У мамы 2 яблока и 3 груши. Каждый день в течение 5 дней она даёт сыну
- 14. Решение задач по теме «Перестановки без повторений и с повторениями» Сколькими различными способами можно усадить за
- 15. РАЗМЕЩЕНИЯ Размещения без повторений — комбинаторные соединения, составленные из n элементов по m. При этом два
- 16. В звене 12 человек. Требуется выбрать звеньевого, санитара, командира. Сколькими способами это можно сделать? Решение. Сначала
- 17. Размещения с повторениями — комбинаторные соединения, составленные из n элементов по m. При этом каждый из
- 18. Примеры. У мамы 2 яблока и 3 груши. Каждый день в течение 5 дней она даёт
- 19. СОЧЕТАНИЯ Сочетания без повторений — комбинаторные соединения из n элементов по k, составленные из этих элементов
- 20. Число k-подмножеств в n-множестве Х называют сочетаниями из n по k. Число таких сочетаний
- 21. Задача У Робина-Бобина Барабека 40 соседей. Он решил пригласить 2 из них на обед. Сколько у
- 22. Сочетания с повторениями — комбинаторные соединения из n элементов по m, составленные из этих элементов без
- 23. Задачи С кондитерском отделе продаются пирожные четырех сортов: Наполеоны, эклеры, песочные и слоёные. Сколькими способами можно
- 24. Сравнительно-сопоставительный анализ формулировок
- 25. Различие между перестановками, размещениями, сочетаниями В случае перестановок берутся все элементы и изменяется только их местоположение.
- 26. Типичные задачи, в которых обычно путаются учащиеся
- 29. Комбинаторные задачи бывают самых разных видов. Однако, большинство задач решается с помощью двух основных правил —
- 30. Если некоторый объект A можно выбрать m способами, а другой объект В можно выбрать n способами,
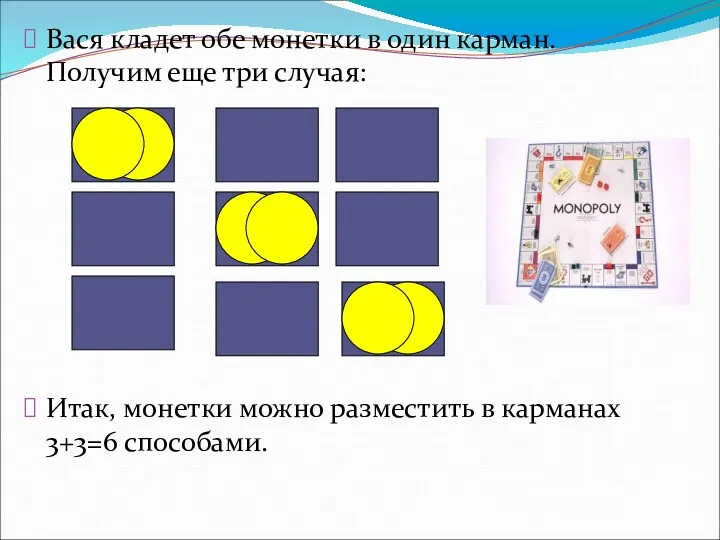
- 31. Задача. У Васи на куртке три кармана. Каким числом способов он может положить в эти карманы
- 32. Решение. Так как монетки одинаковые, и если мы будем применять правило умножения, то некоторые способы учтем
- 33. Вася кладет обе монетки в один карман. Получим еще три случая: Итак, монетки можно разместить в
- 34. Данная задача разбивается на два частных случая, которые не могут происходить одновременно. В итоге надо сложить
- 35. Задача Имеется 8 шаров: в 1 ящик положили 5 шт., а во 2 - 3 шт.
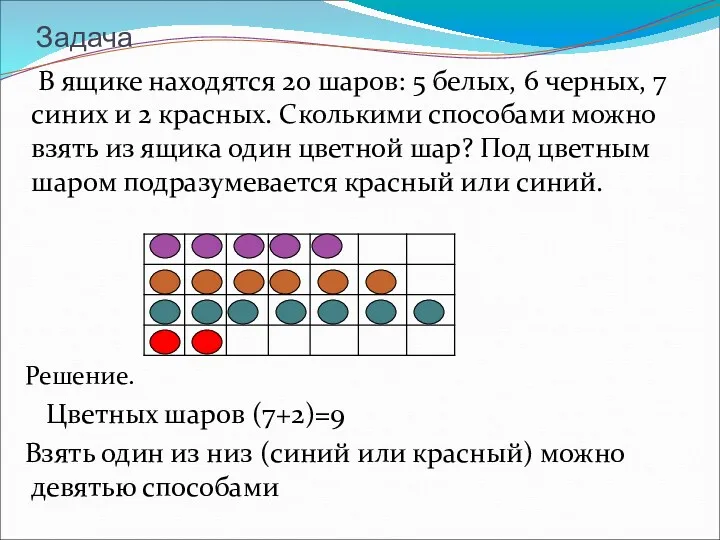
- 36. Задача В ящике находятся 20 шаров: 5 белых, 6 черных, 7 синих и 2 красных. Сколькими
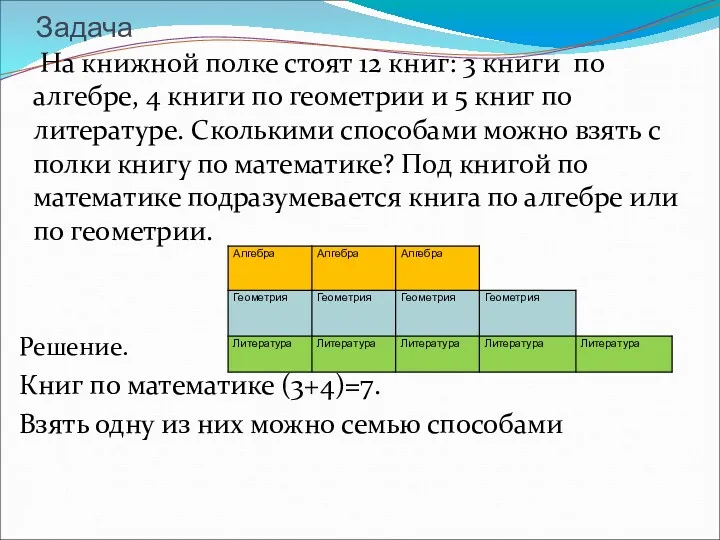
- 37. Задача На книжной полке стоят 12 книг: 3 книги по алгебре, 4 книги по геометрии и
- 38. Задача В олимпиаде участвовало 7 девочек и 18 мальчиков. Сколько существует различных вариантов для получения первого
- 39. Если объект А можно выбрать m способами и если после каждого такого выбора объект В можно
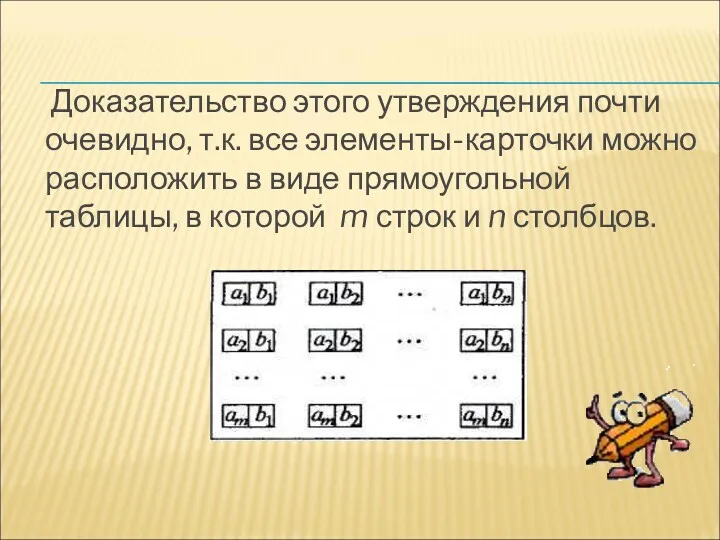
- 40. Доказательство этого утверждения почти очевидно, т.к. все элементы-карточки можно расположить в виде прямоугольной таблицы, в которой
- 41. Множество А×В×С, состоящее из упорядоченных троек, содержит mnр элементов (р - число элементов в множестве С).
- 42. Пусть имеется n элементов и требуется выбрать один за другим некоторые p элементов. Если первый элемент
- 43. Множество А1×А2×...×Ар состоит элементов, где n1- число элементов в А1, n2 - в А2 и т.д.
- 44. Пусть объект а1 можно выбрать n1, различными способами, после каждого выбора объекта а1 объект а2 можно
- 45. Доказательство: если Ак - множество состояний, из которых выбирается объект ак, то nк - число элементов
- 46. Задача Сколькими способами можно выбрать гласную и согласную из слова «МИНУС». Решение. согласные гласные Каждому выбору
- 47. Задача Сколько существует пятизначных чисел, делящихся на 10 без остатка? Решение. Всего вариантов имеем 9*10*10*10=9000
- 48. Задача В высшей лиге первенства по футболу участвуют 16 команд. Разыгрываются 3 медали: золотая, серебряная и
- 49. Пусть а1 - первая буква слова, тогда ее можно выбрать 8 способами, т.е. n1 = 8;
- 50. Задача Пусть ак - к -я буква слова (к =1,2,3,4). Тогда n1 = 8,n2 = 7,
- 51. Задача Дима сложил квадратный листок бумаги пополам, потом еще раз и еще раз. В центре того,
- 52. Задача В коридоре висят три лампочки. Сколько имеется различных способов освещения коридора? Решение. Для каждой лампочки
- 53. Задача В 1 ящике 5 зелёных, а во 2 ящике 3 красных шара. Сколькими способами можно
- 54. Задача От Кащея до Бабы-Яги ведут три дороги, а от Бабы-Яги до Кикиморы - две дороги.
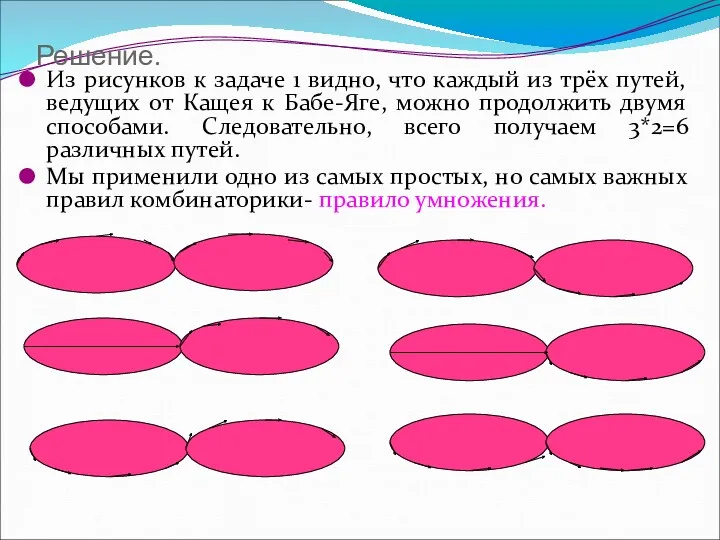
- 55. Решение. Из рисунков к задаче 1 видно, что каждый из трёх путей, ведущих от Кащея к
- 56. Задача Сколькими способами можно расположить 4 шашки на нарисованной доске так, чтобы никакие две из них
- 57. Задача Имеется 6 перчаток различных размеров. Сколькими способами можно выбрать из них одну перчатку на левую
- 58. Сколькими способами могут быть распределены золотая и серебряная медали по итогам олимпиады, если число команд 15?
- 59. Задача Гера, Афина и Афродита попросили Париса не только назвать самую красивую из них, но и
- 60. Задачи по теме «Правило произведения» Сколькими способами можно выбрать гласную и согласную буквы из слова «
- 61. Решение комбинаторных задач Задачу можно назвать комбинаторной, если ее решением является перебор элементов некоторого конечного множества.
- 62. Для того, чтобы решить задачу по комбинаторике, необходимо сначала понять её смысл, то есть, представить мысленно
- 63. Если же комбинаторная задача содержит ряд ограничений, налагающихся на соединения, то нужно понять, как влияют или
- 64. В том случае, если трудно сразу определить какие-либо важные моменты задачи, то не плохо было бы
- 65. Когда комбинаторная задача состоит из различных комбинаций элементарных задач, то нужно просто разбить задачу на подзадачи.
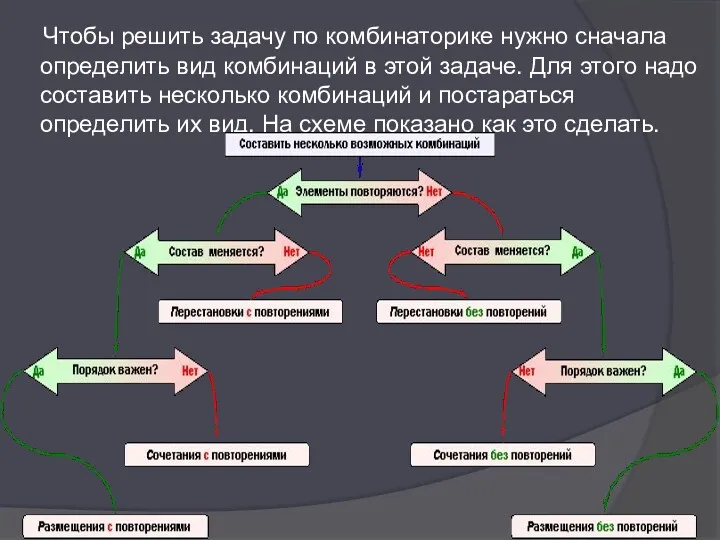
- 66. Чтобы решить задачу по комбинаторике нужно сначала определить вид комбинаций в этой задаче. Для этого надо
- 67. Шпаргалка Пусть требуется выполнить одно за другим k действий. Если первое действие можно выполнить n1 способами
- 68. Задача Сколькими способами можно выбрать на шахматной доске белый и черный квадраты, не лежащие на 1
- 69. Задача Какое максимальное число точек пересечения могут иметь восемь окружностей ? Решение. Две окружности могут пересечься
- 70. Задача. У одного человека есть 7 книг по математике, у другого- 9 книг. Сколькими способами они
- 71. Задача 15 пронумерованных биллиардных шаров разложенные по 6 лузам. Сколькими способами это можно сделать? Решение. Имеем
- 72. Элемент а может быть выбран тремя способами (3 офицера), элемент b(2 сержанта из 6) можно выбрать
- 73. Задача Сколькими способами можно поставить на шахматную доску белую и черную ладью так, чтобы они не
- 74. Задача Сколькими способами можно поставить на доску восемь ладей так, чтобы они не били друг друга?
- 75. Продолжение решения задачи Если же считать ладьи различными (как в примере 3), то число перестановок ладей
- 76. Задача Сколь различных слов можно получить, переставляя буквы слова «комбинаторика»?
- 77. Решение В слове «комбинаторика» 13 букв. Если бы все они были различны, то, переставляя их, можно
- 78. Задача Сколько существует четырехзначных чисел, у которых все цифры нечетные? Сколько существует четырехзначных чисел, в записи
- 79. 2) Все четырехзначные числа, а их 9999-999=9000, делятся на две группы: те, в записи которых все
- 80. Задача Сколько различных пар можно образовать из 28 костей домино так, чтобы кости, входящие в пару,
- 81. Выбор пары костей — это выбор двух карточек вида a1b1, a2b2, где можно считать, что а
- 82. Пример 9. Сколько шестизначных чисел, кратных 5, можно составить из цифр 0, 1,2, ..., 9 при
- 83. Последней цифрой искомого числа может быть 0 или 5. В первом случае остальные пять цифр можно
- 84. Задача Хоккейная команда состоит из 2 вратарей, 7 защитников и 10 нападающих. Сколькими способами тренер может
- 85. Задача На плоскости проведены n прямых, среди которых нет ни одной пары параллельных прямых и ни
- 86. Задача Для проведения письменного экзамена по комбинаторике надо составить 4 варианта по 7 задач в каждом.
- 87. По правилу произведения получаем число Но так как варианты равноправны, то полученное число надо разделить на
- 89. Задача Найти n, если известно, что в разложении (1 + x) коэффициенты при х и х
- 90. Решение. В n-й строке треугольника Паскаля два коэффициента равны в том и только том случае, когда
- 91. Следовательно, равно тогда и только тогда, когда 12 = n-5, т.е. n= 17. Ответ: n =
- 92. Задача Найти коэффициент при х в разложении (1 + х +х ) .
- 93. В силу формулы = Так как уравнение 5k2 + 9к3 =19 имеет только одно решение в
- 94. 2) Обозначим через . Тогда Рассмотрим k-е слагаемое (0≤k≤30): Такое слагаемое будет содержать х , если
- 95. Комбинаторика является древнейшей и, возможно, ключевой ветвью математики. В математике есть задачи, в которых требуется из
- 96. Термин "комбинаторика" был введён в математический обиход знаменитым Лейбницем. Готфрид Вильгельм Лейбниц(1.07.1646 - 14.11.1716) - всемирно
- 97. Так, Леонард Эйлер рассматривал задачи о разбиении чисел, о паросочетаниях, о циклических расстановках, о построении магических
- 98. Список использованной литературы: 1) Газета "Математика в школе" - № 15, 16, 17 2004г. 2) В.Н.
- 100. Скачать презентацию



























































































 Решение неравенств второй степени с одной переменной
Решение неравенств второй степени с одной переменной Метод координат
Метод координат Математика 4 класс. Тест
Математика 4 класс. Тест Умножаем и делим на 10. 2 класс
Умножаем и делим на 10. 2 класс Показательная функция
Показательная функция Решение задач на готовых чертежах. Теорема Пифагора
Решение задач на готовых чертежах. Теорема Пифагора Понятие одночлена. Стандартный вид одночлена
Понятие одночлена. Стандартный вид одночлена Свойства прямой и обратной функций
Свойства прямой и обратной функций Трансцедентные числа π и е
Трансцедентные числа π и е Деление с остатком
Деление с остатком урок по программе Школа России 4 класс. Задачи на движение. Закрепление
урок по программе Школа России 4 класс. Задачи на движение. Закрепление Параллельность прямых и плоскостей
Параллельность прямых и плоскостей Формальные логические теории. Исчисление предикатов
Формальные логические теории. Исчисление предикатов Нахождение целого по его части на основе формального правила
Нахождение целого по его части на основе формального правила Подобные треугольников. Признаки подобия треугольников. 8 класс
Подобные треугольников. Признаки подобия треугольников. 8 класс Дії з двоцифровими числами. Творча робота над задачею. Урок №128
Дії з двоцифровими числами. Творча робота над задачею. Урок №128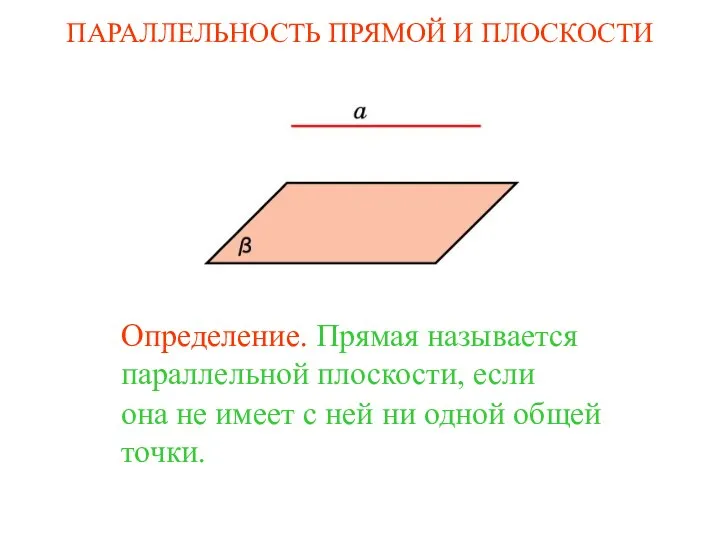 Параллельность прямой и плоскости
Параллельность прямой и плоскости Начальные сведения из стереометрии
Начальные сведения из стереометрии Прибавить и вычесть число 5.
Прибавить и вычесть число 5. Сумма n-первых членов арифметической прогрессии
Сумма n-первых членов арифметической прогрессии Решение систем уравнений способом сложения
Решение систем уравнений способом сложения Начертательная геометрия. Способы преобразования проекций. (Лекция 3)
Начертательная геометрия. Способы преобразования проекций. (Лекция 3) Движение. Виды движения
Движение. Виды движения Презентация к уроку математики во 2 классе по теме Приёмы вычислений для случаев вида 36 + 2, 36 + 20
Презентация к уроку математики во 2 классе по теме Приёмы вычислений для случаев вида 36 + 2, 36 + 20 Функция у=ах² , её свойства и график. 8 класс
Функция у=ах² , её свойства и график. 8 класс Великие педагоги и математики
Великие педагоги и математики ЕГЭ - 2017 по математике. Базовый уровень. Задачи на логику и смекалку
ЕГЭ - 2017 по математике. Базовый уровень. Задачи на логику и смекалку Производная показательной и логарифмической функций
Производная показательной и логарифмической функций