Содержание
- 2. Если решение системы единственное, то система линейных уравнений называется определенной. В случае, когда решение совместной системы
- 3. ТЕОРЕМА КРАМЕРА Если главный определитель системы линейных алгебраических уравнений Δ отличен от нуля, то эта система
- 4. Формулы Крамера где Δj=0 (j=1,…,n) - определители, образованные из главного определителя СЛУ Δ заменой j-го столбца
- 5. Однородные системы ЛУ (ОСЛУ) Система уравнений с нулевыми свободными членами называется однородной, в противном случае –
- 6. Критерий существования нетривиального решения однородной системы (ОСЛУ) Теорема. Для того, чтобы однородная квадратная система линейных уравнений
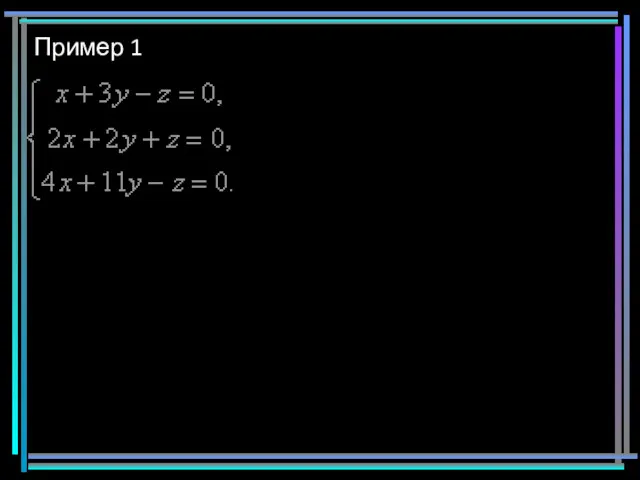
- 7. Пример 1
- 8. Пример 1 Определитель системы не равен нулю, значит ОСЛУ имеет единственное тривиальное решение x=y=z=0. Раскладываем определитель
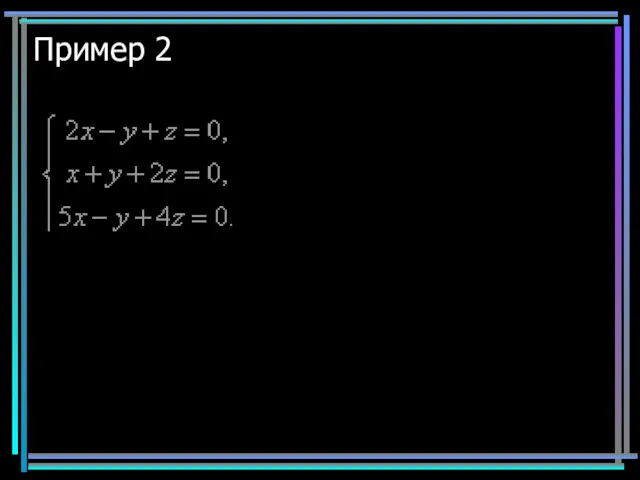
- 9. Пример 2
- 10. Пример 2 Бесконечное множество решений
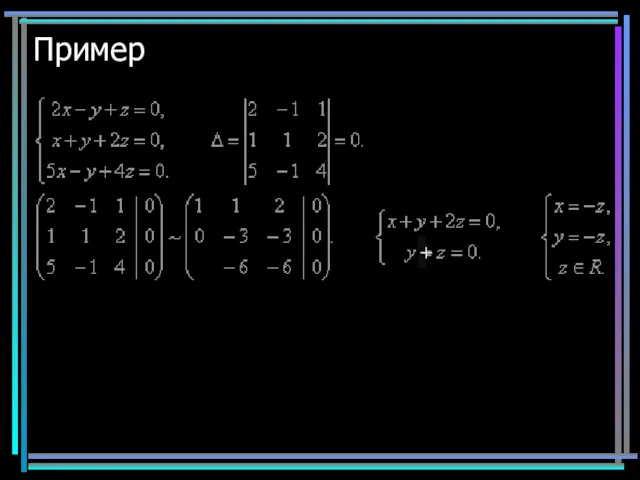
- 11. Пример 2 Ставим 2 строку на место 1-ой, умножаем ее на (-2) и складываем со 2-ой.
- 12. Пример 2 Ставим 2 строку на место 1-ой, умножаем ее на (-2) и складываем со 2-ой.
- 13. Пример +
- 14. Решение систем линейных уравнений матричным методом или методом обратной матрицы
- 15. Обратная матрица Пусть A — квадратная матрица порядка nхn: Если существует квадратная матрица X той же
- 16. Пример
- 17. Невырожденная матрица ― квадратная матрица ― квадратная матрица, определитель ― квадратная матрица, определитель которой отличен от
- 18. Всякая невырожденная матрица A имеет единственную обратную матрицу. Aij — алгебраическое дополнение элемента aij матрицы A.
- 19. Свойства обратной матрицы (справедливы для любых невырожденных матриц): (A·B)−1 = B−1·A−1; (A−1)−1= A; E−1=E; A·A−1·A =
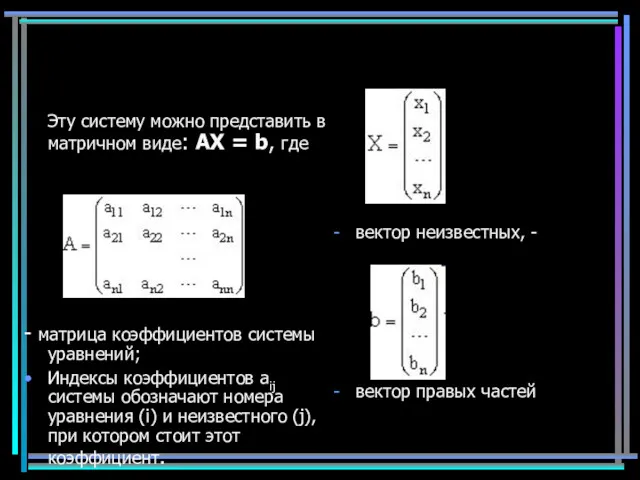
- 20. Пусть задана СЛАУ следующего вида:
- 21. Эту систему можно представить в матричном виде: AX = b, где - матрица коэффициентов системы уравнений;
- 22. A·X = b А-1·A· X=А-1·b E · X=А-1·b X=А-1·b
- 23. Система уравнений называется совместной, если она имеет хотя бы одно решение, в противном случае система несовместна.
- 24. Порядок операций при вычислении обратной матрицы:
- 26. Матрица, обратная к диагональной матрице — диагональная матрица. Пример –доказать
- 27. Матрица, обратная к треугольной матрице — треугольная матрица
- 29. Найти решение системы уравнений: 4x1+2x2= 4 x1+x2= 2
- 30. Найти решение системы уравнений: 3x1-5x2= 22 x1+4x2= 5
- 32. Скачать презентацию
















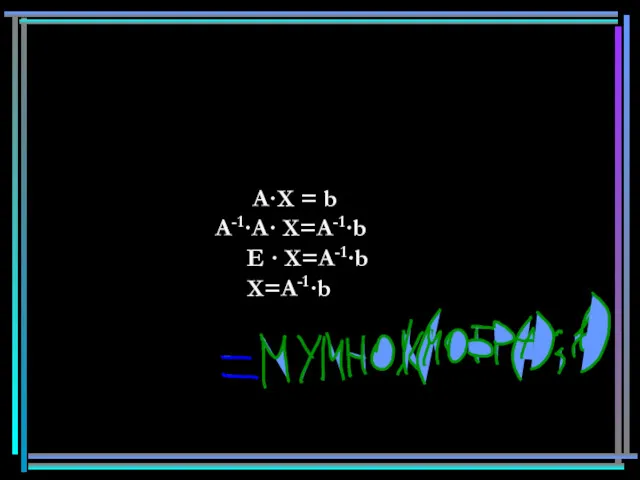








 Перенос графика функции у=ах2 вдоль осей координат
Перенос графика функции у=ах2 вдоль осей координат Дидактические игры в тригонометрии
Дидактические игры в тригонометрии Основные формулы метода координат в пространстве. Урок №1. 11 класс
Основные формулы метода координат в пространстве. Урок №1. 11 класс Устная работа. Логарифмы. 10 класс
Устная работа. Логарифмы. 10 класс Урок - экскурсия. 1 класс. Математика
Урок - экскурсия. 1 класс. Математика Презентация Давай посчитаем! Счет в пределах 10
Презентация Давай посчитаем! Счет в пределах 10 Замечательные точки треугольника
Замечательные точки треугольника Решение задач С2. Нахождение расстояния между двумя скрещивающимися прямыми
Решение задач С2. Нахождение расстояния между двумя скрещивающимися прямыми мастер-класс для учителей начальной школы Магические квадраты
мастер-класс для учителей начальной школы Магические квадраты Аксиомы геометрии
Аксиомы геометрии teoriya_avtomaticheskogo_upravleniya_Polulah_parth2
teoriya_avtomaticheskogo_upravleniya_Polulah_parth2 Математикалық поезд
Математикалық поезд Формула полной вероятности
Формула полной вероятности Градусная мера дуги окружности
Градусная мера дуги окружности Сумма углов треугольника
Сумма углов треугольника ОГЭ. Геометрия на клетчатой бумаге
ОГЭ. Геометрия на клетчатой бумаге Параллельное проектирование
Параллельное проектирование Экстремум функции нескольких переменных. (Лекция 4)
Экстремум функции нескольких переменных. (Лекция 4) Отношения двух чисел, двух величин
Отношения двух чисел, двух величин Раскрытие скобок
Раскрытие скобок Показательные и логарифмические неравенства. Задание для устного счета
Показательные и логарифмические неравенства. Задание для устного счета Действия с десятичными дробями
Действия с десятичными дробями Матрицы. Определители
Матрицы. Определители Как писать цифры. Математика 1 класс
Как писать цифры. Математика 1 класс Арифметическая и геометрическая прогрессии
Арифметическая и геометрическая прогрессии Разложение многочлена на множители с помощью формул квадрата суммы и квадрата разности двух выражений
Разложение многочлена на множители с помощью формул квадрата суммы и квадрата разности двух выражений Математический тренажер по решению задач на нахождение периметра.
Математический тренажер по решению задач на нахождение периметра. Случаи вычитания 16 -
Случаи вычитания 16 -