Содержание
- 2. Учебник: А.Г. Мордкович, П.В. Семенов. Алгебра-9. § 19. Статистика- дизайн информации (3 часа) Группировка информации. Табличное
- 3. Цели темы: Образовательные: проверка умения учащихся: изображать результаты экспериментов, наблюдений, опросов в виде таблиц, графиков, диаграмм,
- 4. Группировка информации. Табличное представление информации. Цели урока: - Формировать умение использовать методы обработки статистических данных. -
- 5. Как только человеку в его деятельности потребовались количественные характеристики, то есть числа, тут же появилась статистика.
- 6. Сначала возникли демографическая статистика, медицинская статистика, экономическая статистика, потом – метеорологическая, биологическая, финансовая, налоговая и т.д.
- 7. В XX веке появилась математическая статистика, обладающая универсальными методами сбора, хранения и обработки информации для выработки
- 8. Порядок преобразований первоначально полученной информации таков: 1. сначала данные измерений упорядочивают и группируют; 2. затем составляют
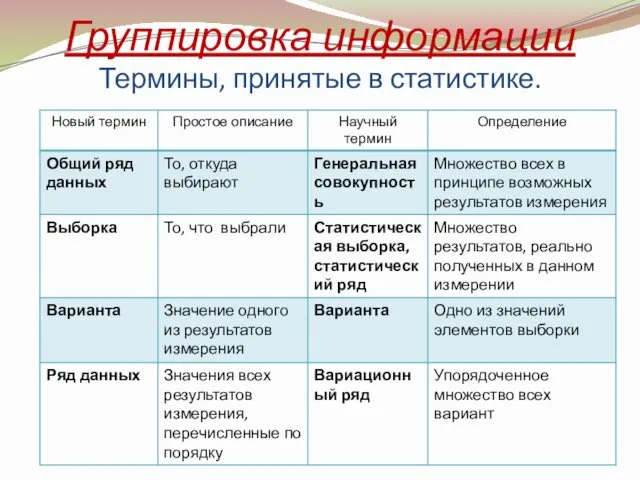
- 9. Группировка информации Термины, принятые в статистике.
- 10. Пример(№19.4). В девятых классах «А» и «Б» измерили рост 50 учащихся. Получили следующие результаты: а)Каков общий
- 11. Определение. Если среди всех данных конкретного измерения одна из вариант встретилась k раз, то число k
- 12. Пример(№19.11). 30 абитуриентов на четырех вступительных экзаменах набрали в сумме такие количества баллов( оценки на экзаменах
- 13. в) Какова кратность варианты 13 в измерении из пункта б), варианты 14 , варианты 15 ?
- 14. При общей оценке данных выборки часто находят частоту варианты: Частоты всех вариант удобно приписывать следующей строкой
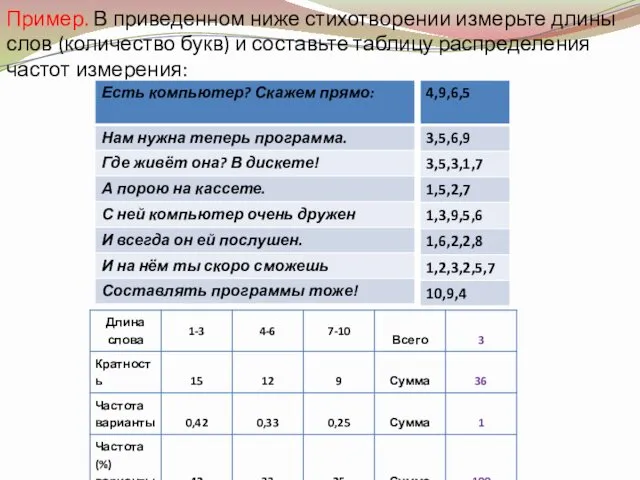
- 15. Пример. В приведенном ниже стихотворении измерьте длины слов (количество букв) и составьте таблицу распределения частот измерения:
- 16. Домашнее задание: § 19, пункты 1и 2, № 19.3, 19.5
- 17. Доп. задание. При выборочной переписи населения в 20 квартирах были получены следующие сведения о годах рождения
- 19. Скачать презентацию














 Презентация по математике Умножение в Простоквашино
Презентация по математике Умножение в Простоквашино Нарушения предпосылок МНК
Нарушения предпосылок МНК Теория судна. Морское нерегулярное волнение
Теория судна. Морское нерегулярное волнение О великом Пифагоре
О великом Пифагоре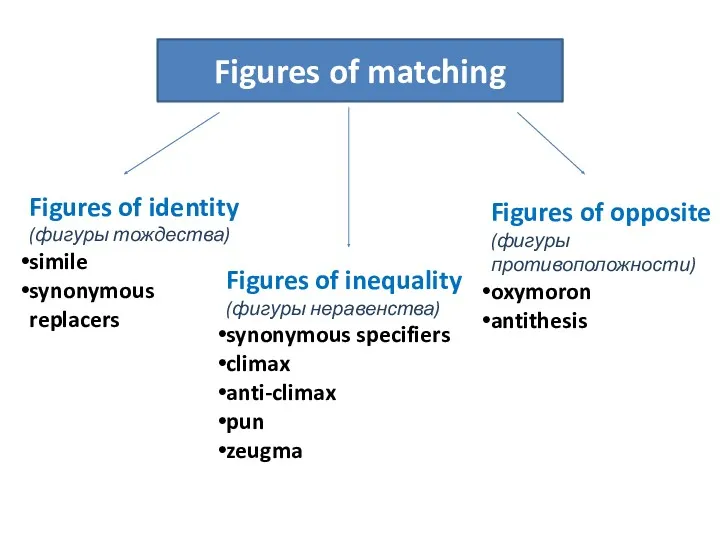 Figures of matching
Figures of matching Тест по теме: Параллельность плоскостей
Тест по теме: Параллельность плоскостей Урок по математике на тему Таблица умножения на 2
Урок по математике на тему Таблица умножения на 2 Туындының көмегімен функцияны зерттеу және оның графигін салу
Туындының көмегімен функцияны зерттеу және оның графигін салу Позициялық және метрикалық есептер
Позициялық және метрикалық есептер Многогранники. Виды многогранников
Многогранники. Виды многогранников Логарифмы. Логарифмическая функция. 11 класс
Логарифмы. Логарифмическая функция. 11 класс Округлення десяткових дробів
Округлення десяткових дробів Понятие первообразной. Неопределенный интеграл
Понятие первообразной. Неопределенный интеграл Умножение и деление на 3. Треть числа.
Умножение и деление на 3. Треть числа. Презентация к уроку математики в 4 классе по теме Единицы времени. Век
Презентация к уроку математики в 4 классе по теме Единицы времени. Век Свойства тройных интегралов
Свойства тройных интегралов Представление трехзначных чисел в виде суммы разрядных слагаемых
Представление трехзначных чисел в виде суммы разрядных слагаемых Делимость произведения
Делимость произведения Применение различных способов разложения многочлена на множители. 7 класс
Применение различных способов разложения многочлена на множители. 7 класс Презентация-тренажёр по таблице умножения
Презентация-тренажёр по таблице умножения Углы, связанные с окружностью. Тест
Углы, связанные с окружностью. Тест Ученье с увлечением нужно всем без исключения»/5кл/
Ученье с увлечением нужно всем без исключения»/5кл/ Умножение натуральных чисел и его свойства. 5 класс
Умножение натуральных чисел и его свойства. 5 класс Подготовка к ОГЭ по геометрии
Подготовка к ОГЭ по геометрии Масса
Масса Веселый зоопарк. Координаты
Веселый зоопарк. Координаты Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Отношением отрезков AB и CD называется отношение их длин
Отношением отрезков AB и CD называется отношение их длин