Слайд 2

ВИДЫ МНОГОГРАННИКОВ
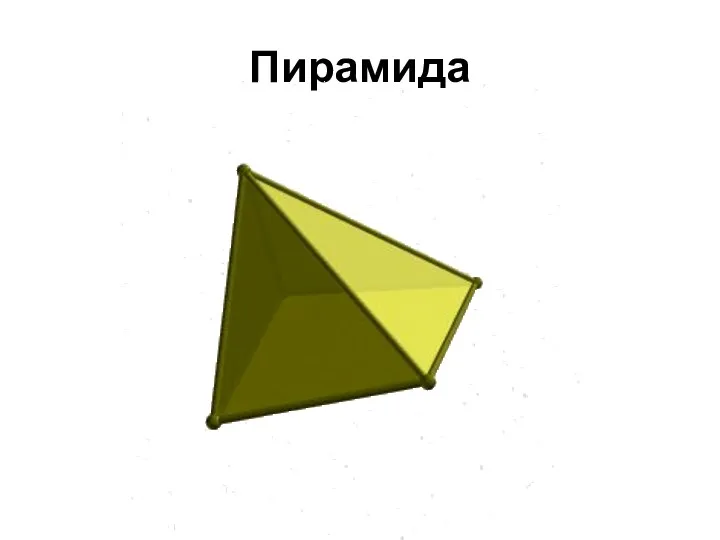
1. Пирамида - это многогранник, одна грань которого многоугольник, а
остальные грани - треугольники с общей вершиной. Пирамида называется правильной, если в основании лежит правильный многоугольник и высота пирамиды проходит через центр многоугольника. Пирамида называется усеченной, если вершина её отсекается плоскостью
Слайд 3
Слайд 4
Слайд 5

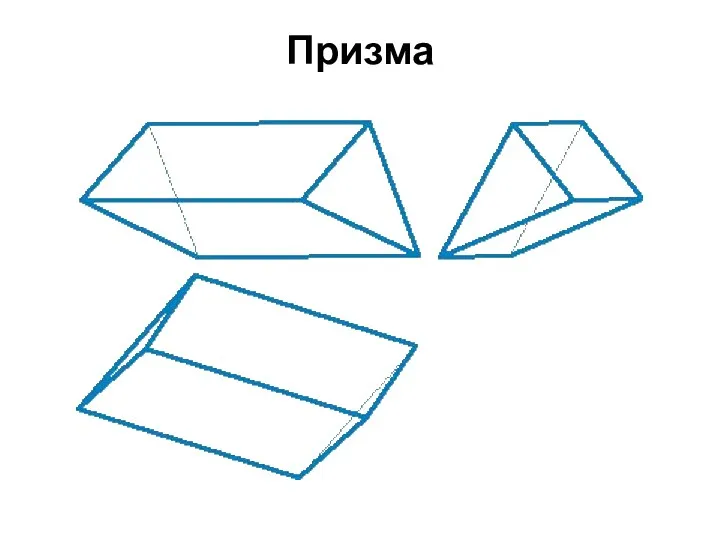
Призма
многоугольник, две грани которого (основания призмы) представляют собой равные многоугольники
с взаимно параллельными сторонами, а все другие грани параллелограммы. Призма называется прямой, если её ребра перпендикулярны плоскости основания. Если основанием призмы является прямоугольник, призму называют параллелепипедом
Слайд 6

Слайд 7
Слайд 8
Слайд 9
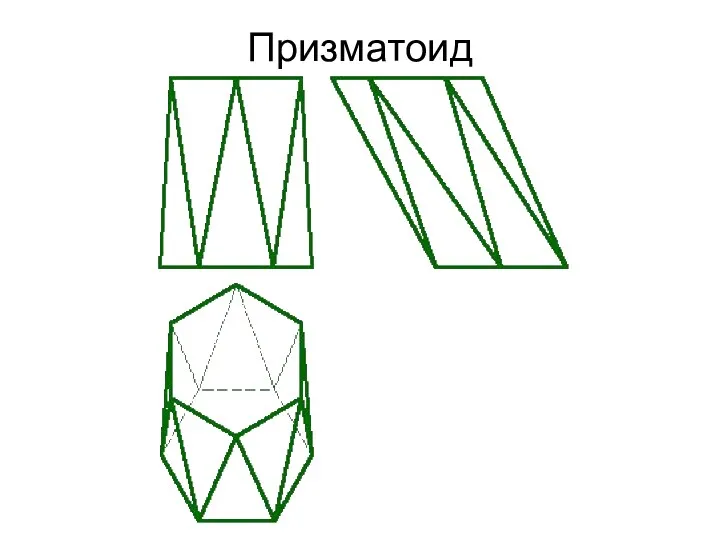
Слайд 10

Тела Платона
. Многогранник, все грани которого представляют собой правильные и равные
многоугольники, называют правильными Углы при вершинах такого многогранника равны между собой.
Существует пять типов правильных многогранников. Эти многогранники и их свойства были описаны более двух тысяч лет назад древнегреческим философом Платоном, чем и объясняется их общее название.
Слайд 11

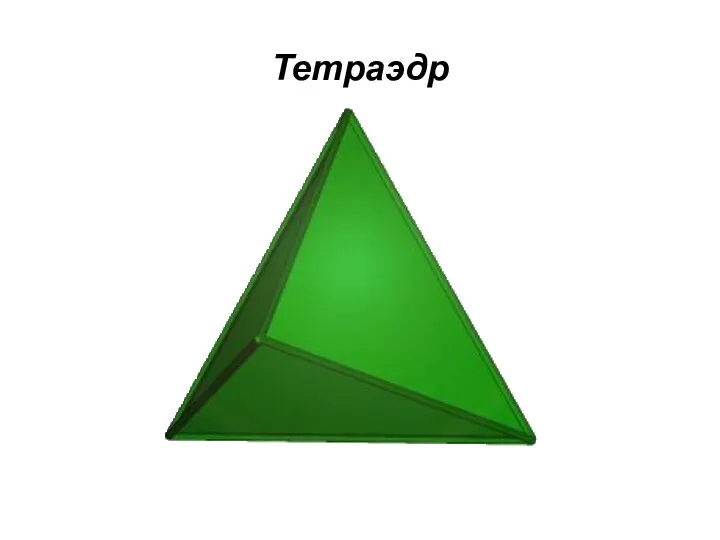
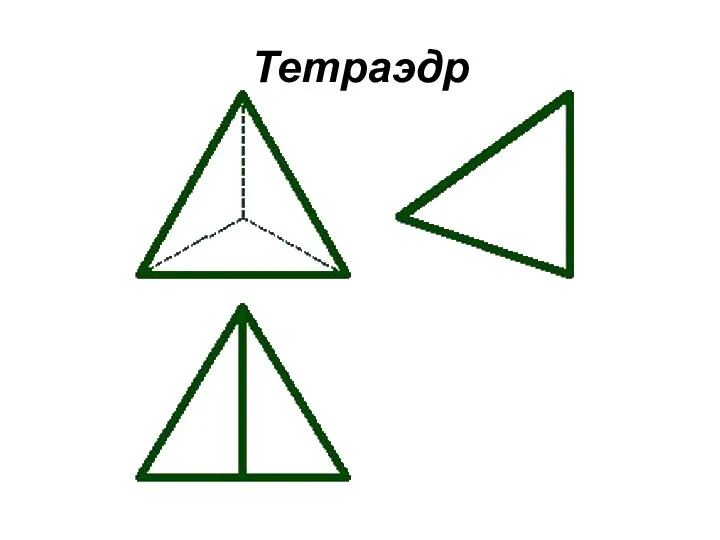
Тетраэдр
Правильный четырехгранник.
Он ограничен четырьмя равносторонними треугольниками (это правильная
треугольная пирамида).
Слайд 12
Слайд 13
Слайд 14

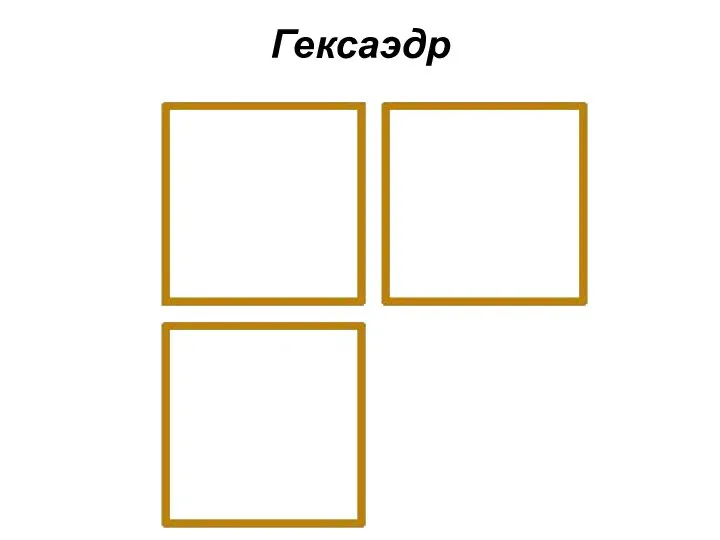
Гексаэдр
Правильный шестигранник.
Это куб состоящий из шести равных квадратов.
Слайд 15

Слайд 16
Слайд 17

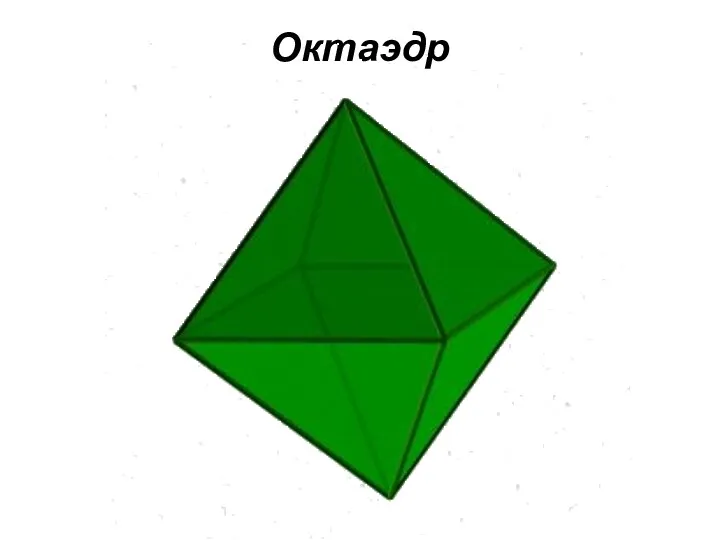
Октаэдр
правильный восьмигранник.
Он состоит из восьми равносторонних и равных между
собой треугольников, соединенных по четыре у каждой вершины
Слайд 18
Слайд 19
Слайд 20

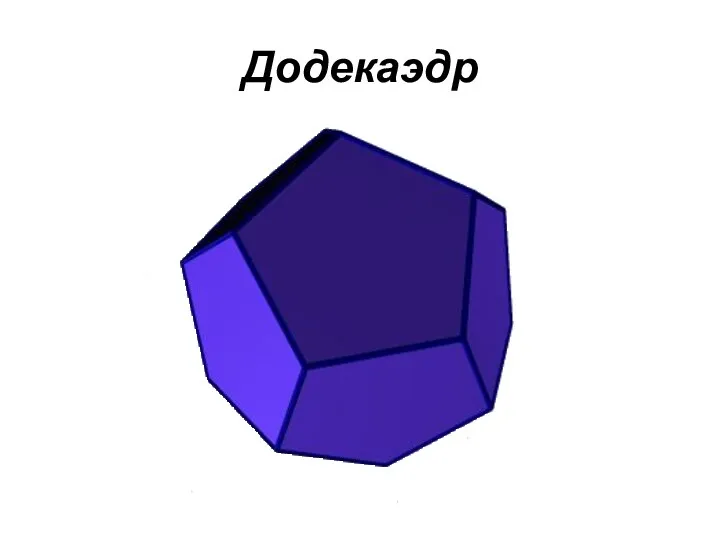
Додекаэдр
правильный двенадцатигранник, состоит из двенадцати правильных и равных пятиугольников, соединенных
по три около каждой вершины
Слайд 21
Слайд 22
Слайд 23

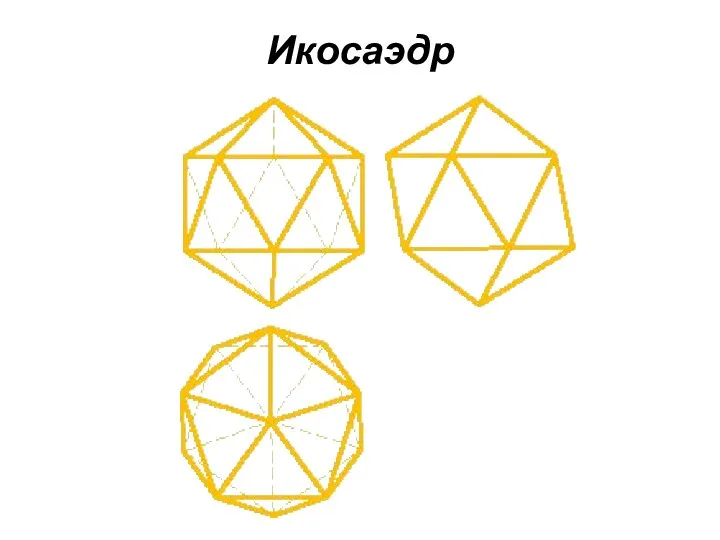
Икосаэдр
состоит из 20 равносторонних и равных треугольников, соединенных по пять
около каждой вершины
Слайд 24

Слайд 25
Слайд 26

Звездчатые формы и соединения тел Платона.
Кроме правильных выпуклых многогранников существуют
и правильные выпукло-вогнутые многогранники. Их называют звездчатыми (самопересекающимися). Рассматривая пересечения продолжения граней Платоновых тел, мы будем получать звездчатые многогранники
Слайд 27

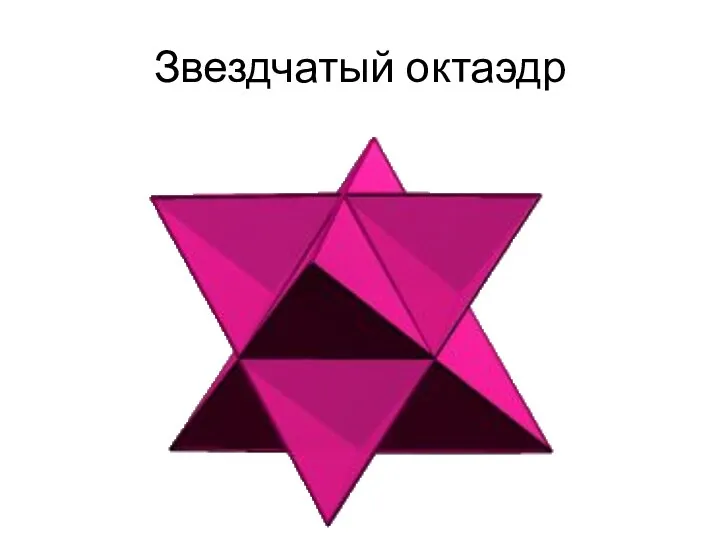
Звездчатый октаэдр
восемь пересекающихся плоскостей граней октаэдра отделяют от пространства новые
"куски", внешние по отношению к октаэдру. Это малые тетраэдры основания которые совпадают с гранями октаэдра. его можно рассматривать как соединение двух пересекающихся тетраэдров центры которых совпадают с центром исходного октаэдра. Все вершины звездчатого октаэдра совпадают с вершинами некоторого куба, а ребра его являются диагоналями граней (квадратов) этого куба. Дальнейшее продление граней октаэдра не приводит к созданию нового многогранника. Октаэдр имеет только одну звездчатую форму
Слайд 28
Слайд 29

Малый звездчатый додекаэдр
Звездчатый додекаэдр первого продолжения. Он образован продолжением граней
выпуклого додекаэдра до их первого пересечения. Каждая грань выпуклого додекаэдра при продолжении образует правильный звездчатый пятиугольник. Пересекающиеся плоскости граней додекаэдра отделяют от пространства новые "куски", внешние по отношению к додекаэдру. Это двенадцать правильных пятиугольных пирамид, основания которых совпадают с гранями додекаэдра.
Слайд 30

Малый звездчатый додекаэдр
Слайд 31

Слайд 32

Кривая линия
Кривая линия - это множество точек пространства, координаты которых являются
функциями одной переменной.
Термин «кривая» в разных разделах математики определяется по-разному. В начертательной геометрии кривую рассматривают как траекторию, описанную движущей точкой, как проекцию другой кривой, как линию пересечения двух поверхностей, как множество точек, обладающих каким-либо общим для всех их свойством и т.д.
Слайд 33

Кривые линии разделяют на плоские и пространственные.
Плоскими называют такие кривые, все
точки которых лежат в одной плоскости .
Пространственными называют кривые, точки которых не лежат в одной плоскости
Слайд 34

способы задания кривых:
·Аналитический – кривая задана математическим уравнением;
·Графический – кривая задана
визуально на носителе графической информации;
·Табличный – кривая задана координатами последовательного ряда точек
Слайд 35

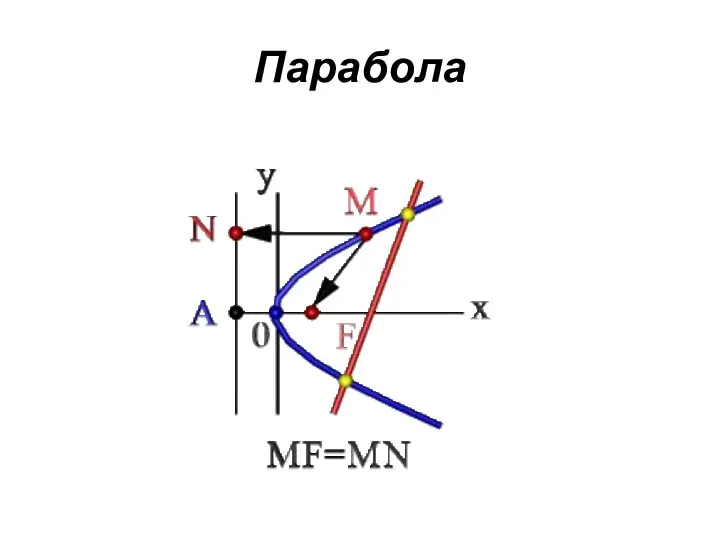
Парабола
кривая второго порядка, прямая пересекает ее в двух точках. При
этом парабола может быть определена как:
-множество точек М(xy) плоскости, расстояние FM которых до определенной точки F этой плоскости (фокуса параболы) равно расстоянию MN до определенной прямой АN - директрисы параболы;
-линия пересечения прямого кругового конуса плоскостью, не проходящей через вершину конуса и параллельная какой либо касательной плоскости этого конуса;
-в прямоугольной системе координат 0ху с началом в вершине параболы и осью 0х направленной по оси параболы уравнение параболы имеет так называемый канонический вид
y2=2px,
где р (фокальный параметр) - расстояние от фокуса до директрисы
Слайд 36
Слайд 37

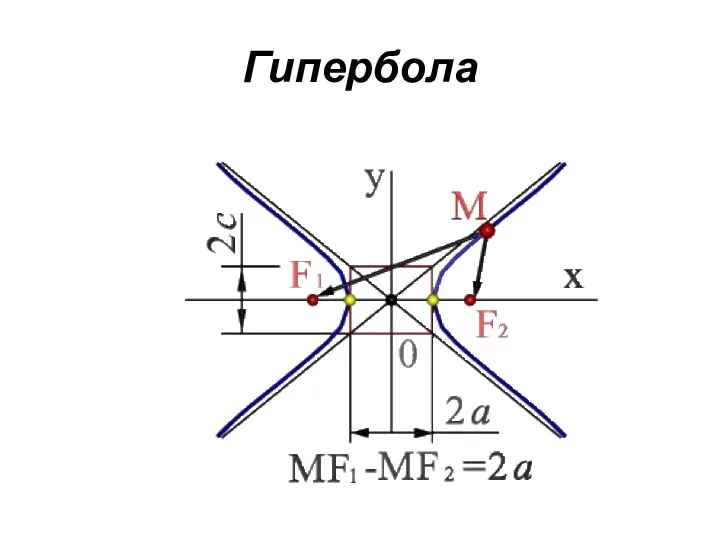
Гипербола
множество точек М плоскости разность (по абсолютной величине) расстояний F1M
и F2M которых до двух определенных точек F1 и F2 этой плоскости (фокусов гиперболы) постоянна:
F1M - F2M=2а<2с
Середина 0 отрезка F1F2 (фокусного расстояния) называется центром гиперболы;
- линия пересечения прямого кругового конуса плоскостью, не проходящей через вершину конуса и пересекающая обе его полости;
- в прямоугольной системе координат 0ху с началом в центре гиперболы, на оси 0х которой лежат фокусы гиперболы уравнение гиперболы имеет так называемый канонический
х2/а2 - у2/в2=1, в2=с2 - а2,
где а и в длинны полуосей гиперболы.
Слайд 38
Слайд 39

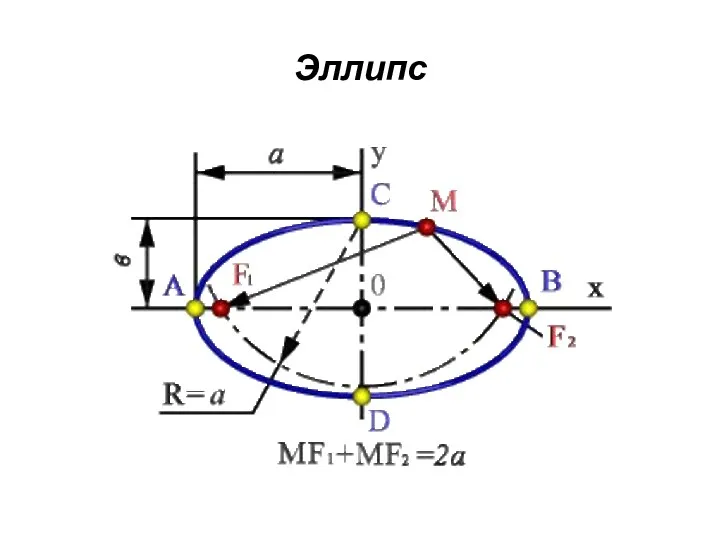
Эллипс
множество точек М плоскости, сумма расстояний МF1 и МF2 которых
до двух определенных точек F1 и F2 (фокусов эллипса) постоянна
МF1+МF2=2а.
Середина 0 отрезка F1F2 (фокусного расстояния)называется центром эллипса;
- линия пересечения прямого кругового конуса плоскостью, не проходящей через вершину конуса и пересекающей все прямолинейные образующие одной полости этого конуса;
- в прямоугольной системе координат 0ху с началом в центре эллипса, на оси 0х которой лежат фокусы эллипса уравнение эллипса имеет следующий вид
х2/а2+у2/в2=1,
где а и в - длинны большой и малой полуосей эллипса. При а=в фокусы F1 и F2 совпадают и указанное уравнение определяет окружность, которая рассматривается как частный случай эллипса
Слайд 40
Слайд 41

СВОЙСТВА ОРТОГОНАЛЬНЫХ ПРОЕКЦИЙ КРИВОЙ ЛИНИИ
1. Проекцией кривой линии является кривая линия;
2.
Касательная к кривой линии проецируется в касательную к её проекции;
3. Несобственная точка кривой проецируется в несобственную точку её проекции;
4. Порядок линии – проекции алгебраической кривой равен порядку самой кривой или меньше;
5. Число узловых точек ( в которых кривая пересекает сама себя) проекции равно числу узловых точек самой кривой.
Слайд 42

Пространственные кривые линии
Пространственные кривые линии в начертательной геометрии обычно рассматриваются
как результат пересечения поверхностей или траекторию движения точки.
Пространственную, так же как и плоскую, кривую линию на чертеже задают последовательным рядом точек.
Классическим примером пространственных кривых линий являются цилиндрическая и коническая винтовые линии.
Смещение точки вдоль образующей за один оборот называется шагом цилиндрической винтовой линии.
Слайд 43
Цилиндрическая винтовая линия
Слайд 44
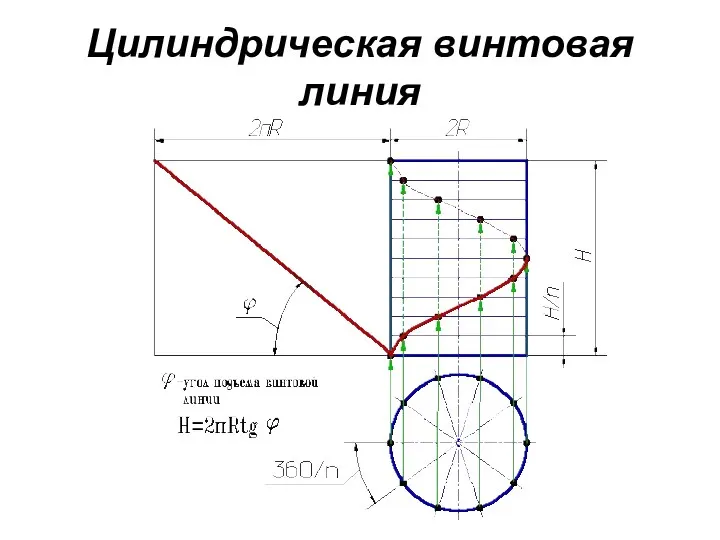
Цилиндрическая винтовая линия
Слайд 45

Коническая винтовая линия
Такую линию описывает точка, которая движется по какой-либо образующей
прямого кругового конуса, вращающегося вокруг своей оси так, что путь пройденный точкой по образующей все время равен углу поворота конуса.
Проекция на ось конуса смещения точки вдоль образующей за один оборот называется шагом конической винтовой линии. Горизонтальной проекцией конической винтовой линии является спираль Архимеда - одна из замечательных плоских кривых линий.
Слайд 46
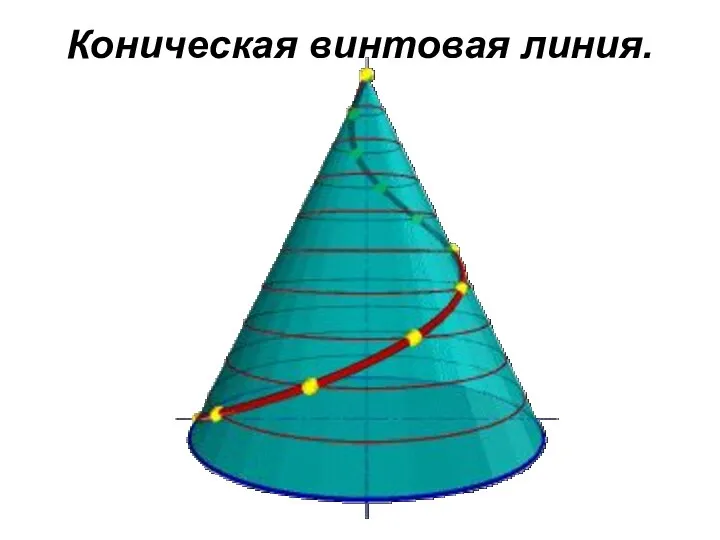
Коническая винтовая линия.













































 Множества. Пересечение и объединение множеств
Множества. Пересечение и объединение множеств презентация к уроку в 4 классе. Тема: Задачи на движение
презентация к уроку в 4 классе. Тема: Задачи на движение Раньше, позже, сначала, потом
Раньше, позже, сначала, потом Презентация к уроку математики 2 класс по УМКШкола России
Презентация к уроку математики 2 класс по УМКШкола России Английский математик Август де Морган
Английский математик Август де Морган Подготовка к ОГЭ. Теория вероятностей (Задание №10)
Подготовка к ОГЭ. Теория вероятностей (Задание №10) Аксиомы стереометрии и следствия из них
Аксиомы стереометрии и следствия из них Стандартный вид числа
Стандартный вид числа Конкурс красоты, ума и таланта. Мисс Математика
Конкурс красоты, ума и таланта. Мисс Математика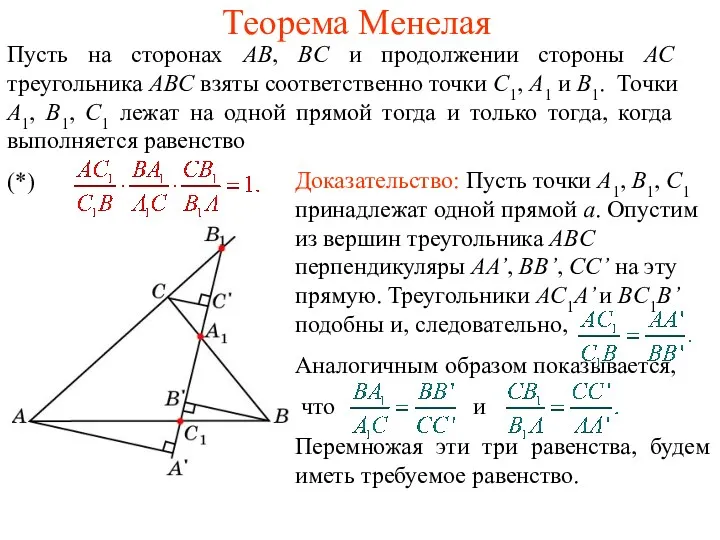 Теоремы Менелая и Чевы
Теоремы Менелая и Чевы Свойства движений. Параллельный перенос
Свойства движений. Параллельный перенос Обзор распространенных тестов зависимость и независимость выборок (не-) и параметрические и тесты корреляции
Обзор распространенных тестов зависимость и независимость выборок (не-) и параметрические и тесты корреляции Обучение решению задач на проценты – путь успешной подготовки к ГИА и ЕГЭ
Обучение решению задач на проценты – путь успешной подготовки к ГИА и ЕГЭ Объемы наклонной призмы, пирамиды, конуса
Объемы наклонной призмы, пирамиды, конуса Применение кейс технологий на уроках математики
Применение кейс технологий на уроках математики Аксиома параллельных прямых
Аксиома параллельных прямых Математическая логика
Математическая логика Статистический смысл выборочных показателей
Статистический смысл выборочных показателей Показательная функция. График функции
Показательная функция. График функции Угол между векторами. Скалярное произведение векторов
Угол между векторами. Скалярное произведение векторов Площади многоугольников. По материалам открытого банка задач ЕГЭ по математике
Площади многоугольников. По материалам открытого банка задач ЕГЭ по математике Особливості організації навчання математики у 2019-2020 н.р
Особливості організації навчання математики у 2019-2020 н.р Практико-ориентированные задачи по математике как средство формирования учебно-познавательных компетенций школьников
Практико-ориентированные задачи по математике как средство формирования учебно-познавательных компетенций школьников Умножение и деление натуральных чисел
Умножение и деление натуральных чисел Площадь. Сравнение площадей
Площадь. Сравнение площадей Презентация Устный счет 4 класс
Презентация Устный счет 4 класс решение неравенств второй степени с помощью графика квадратичной функции
решение неравенств второй степени с помощью графика квадратичной функции Устная работа с текстом на уроках математики
Устная работа с текстом на уроках математики