- Главная
- Математика
- Теорема Пифагора

Содержание
- 2. Пифагор
- 3. Собственно теорема
- 5. Доказательства: Доказательство через подобные треугольники.
- 6. Одним из наиболее популярных в учебной литературе доказательств алгебраической формулировки является доказательство с использованием техники подобия
- 7. Доказательство через равнодополняемость
- 9. Доказательство Евклида
- 10. Идея доказательства Евклида состоит в следующем: попробуем доказать, что половина площади квадрата, построенного на гипотенузе, равна
- 11. Доказательство Леонардо Да Винчи
- 13. Конец
- 16. Скачать презентацию
Слайд 2
Пифагор
Пифагор
Слайд 3
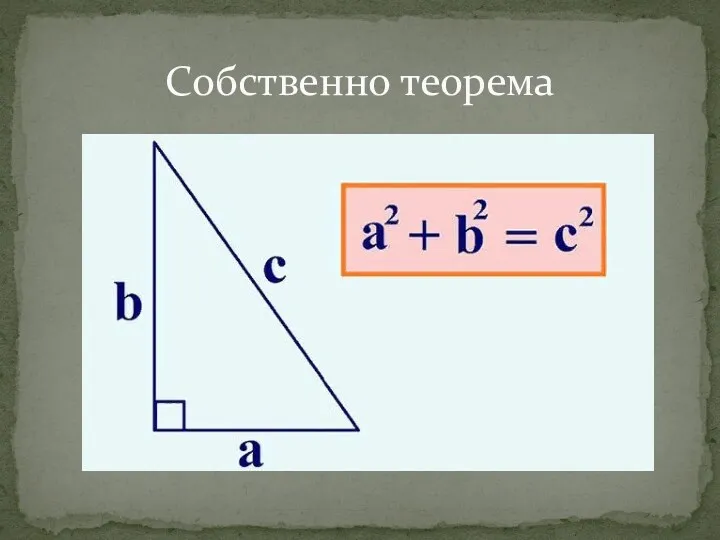
Собственно теорема
Собственно теорема
Слайд 4
Слайд 5
Доказательства:
Доказательство через подобные треугольники.
Доказательства:
Доказательство через подобные треугольники.
Слайд 6
Одним из наиболее популярных в учебной литературе доказательств алгебраической формулировки является
Одним из наиболее популярных в учебной литературе доказательств алгебраической формулировки является
доказательство с использованием техники подобия треугольников, при этом оно почти непосредственно выводится из аксиом и не задействует понятие площади фигуры.
В нём для треугольника ABC с прямым углом при вершине C со сторонами a, b, c, противолежащими вершинам A, B, C, соответственно, проводится высота CH, при этом возникают соотношения подобия: треугольник ABC подобен треугольнику ACH и треугольник АВС подобен CBH, из чего непосредственно следуют соотношения:
В нём для треугольника ABC с прямым углом при вершине C со сторонами a, b, c, противолежащими вершинам A, B, C, соответственно, проводится высота CH, при этом возникают соотношения подобия: треугольник ABC подобен треугольнику ACH и треугольник АВС подобен CBH, из чего непосредственно следуют соотношения:
Слайд 7
Доказательство через равнодополняемость
Доказательство через равнодополняемость
Слайд 8
Слайд 9
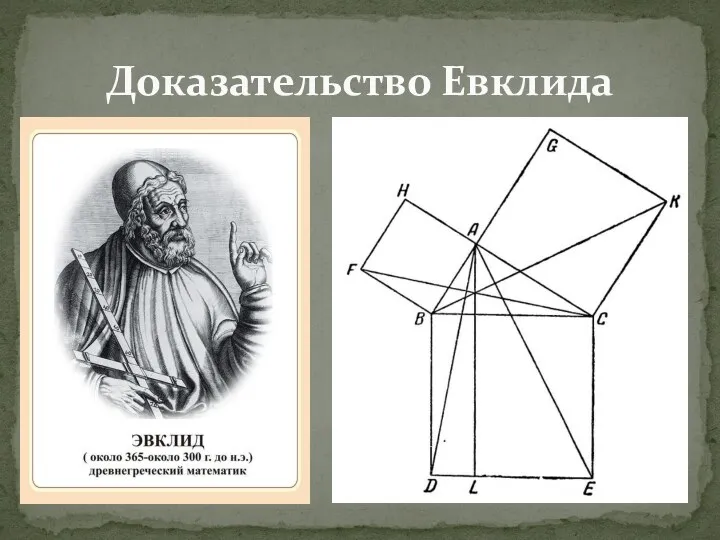
Доказательство Евклида
Доказательство Евклида
Слайд 10
Идея доказательства Евклида состоит в следующем: попробуем доказать, что половина площади
Идея доказательства Евклида состоит в следующем: попробуем доказать, что половина площади
квадрата, построенного на гипотенузе, равна сумме половин площадей квадратов, построенных на катетах, а тогда и площади большого и двух малых квадратов равны. Рассмотрим чертеж слева. На нём мы построили квадраты на сторонах прямоугольного треугольника и провели из вершины прямого угла С луч s перпендикулярно гипотенузе AB, он рассекает квадрат ABIK, построенный на гипотенузе, на два прямоугольника — BHJI и HAKJ соответственно. Оказывается, что площади данных прямоугольников в точности равны площадям квадратов, построенных на соответствующих катетах. Попытаемся доказать, что площадь квадрата DECA равна площади прямоугольника AHJK Для этого воспользуемся вспомогательным наблюдением: Площадь треугольника с той же высотой и основанием, что и данный прямоугольник, равна половине площади заданного прямоугольника. Это следствие определения площади треугольника как половины произведения основания на высоту. Из этого наблюдения вытекает, что площадь треугольника ACK равна площади треугольника AHK (не изображённого на рисунке), которая, в свою очередь, равна половине площади прямоугольника AHJK. Докажем теперь, что площадь треугольника ACK также равна половине площади квадрата DECA. Единственное, что необходимо для этого сделать, — это доказать равенство треугольников ACK и BDA (так как площадь треугольника BDA равна половине площади квадрата по указанному выше свойству). Равенство это очевидно, треугольники равны по двум сторонам и углу между ними. Именно — AB=AK,AD=AC — равенство углов CAK и BAD легко доказать методом движения: повернём треугольник CAK на 90° против часовой стрелки, тогда очевидно, что соответствующие стороны двух рассматриваемых треугольников совпадут (ввиду того, что угол при вершине квадрата — 90°). Рассуждение о равенстве площадей квадрата BCFG и прямоугольника BHJI совершенно аналогично. Тем самым мы доказали, что площадь квадрата, построенного на гипотенузе, слагается из площадей квадратов, построенных на катетах.
Слайд 11
Доказательство Леонардо Да Винчи
Доказательство Леонардо Да Винчи
Слайд 12
Слайд 13
Конец
Конец
Слайд 14











 Логарифмическая функция, ее свойства и график
Логарифмическая функция, ее свойства и график Криптографическая защита информации. Элементы теории чисел. (Лекция 3)
Криптографическая защита информации. Элементы теории чисел. (Лекция 3) Сложение числа б с однозначными числами. 1 класс
Сложение числа б с однозначными числами. 1 класс Сравнение чисел
Сравнение чисел Способы доказательства теоремы Пифагора
Способы доказательства теоремы Пифагора Магический квадрат третьего порядка
Магический квадрат третьего порядка Квадрат суммы и разности двух выражений
Квадрат суммы и разности двух выражений Построение сечений многогранников
Построение сечений многогранников Упрощение выражений
Упрощение выражений Число и цифра 1-10
Число и цифра 1-10 Устная разминка на уроке математики
Устная разминка на уроке математики Действия над обыкновенными дробями
Действия над обыкновенными дробями Правильные и неправильные дроби. 5 класс
Правильные и неправильные дроби. 5 класс Модели статистического прогнозирования
Модели статистического прогнозирования Расчет каналов. Гидравлика
Расчет каналов. Гидравлика Математическая викторина
Математическая викторина Презентации к урокам математики
Презентации к урокам математики Дискретная математика. Деревья. Определения дерева
Дискретная математика. Деревья. Определения дерева тест Составные задачи
тест Составные задачи Площадь параллелограмма
Площадь параллелограмма Образование чисел из одного десятка и нескольких единиц. 1 класс
Образование чисел из одного десятка и нескольких единиц. 1 класс Туындының анықтамасы
Туындының анықтамасы Презентация. Сложение и вычитание в пределах 20.
Презентация. Сложение и вычитание в пределах 20. Великие математики России
Великие математики России Доли. Обыкновенные дроби. 5 класс
Доли. Обыкновенные дроби. 5 класс Трапеция. Свойства, решение задач
Трапеция. Свойства, решение задач Всероссийская проверочная работа по математике
Всероссийская проверочная работа по математике Көрсеткіштік теңсіздіктер
Көрсеткіштік теңсіздіктер