Содержание
- 2. «настоящие» только натуральные числа-древнегреческие математики Введение отрицательных чисел- китайские математики за 2 века до н.э. VII
- 4. XVI в. изучение кубических уравнений ит. математик Н.Тарталья x3=px+q Корень уравнения: x= где u, v- решение
- 5. пример 1 x3=px+q Корень уравнения: x= где u, v- решение системы уравнений x3=9x+28 p=9, q=28 откуда
- 6. пример 2 x3=15x+4 х=4- действительный корень Не имеет решения во множестве действительных чисел x3=px+q Корень уравнения:
- 7. 1545 г. Дж.Кардано (ит.алгебраист)- «чисто отрицательные» 1572 г. Р.Бомбелли (ит.алгебраист)- первые правила арифметических операций 1637 г.
- 8. 1777 г. Л Эйлер (шв.математик) – обозначение i от латинского imaginarius - «мнимый» 1831 г. К.Гаусс
- 9. В течение XVIII в. были решены многие вопросы и прикладные задачи, связанные картография гидродинамика теория жидкости
- 10. Применение комплексных чисел в электротехнике Для расчета цепей постоянного тока Для расчета цепей переменного тока Упрощение
- 11. Навыки, полученные после изучения темы «комплексные числа» Находить модуль и аргумент комплексного числа и комплексное число
- 12. Мнимая единица Мнимая единица- это число, квадрат которого равен –1. i2 = -1 - мнимая единица
- 13. Степени мнимой единицы
- 14. если n:4 (ост.0), то in= 1=i0 если n:4 (ост.1), то in= i=i1 если n:4 (ост.2), то
- 15. Алгебраическая форма комплексного числа Числа вида a+bi, где a,b∈ℝ, i- мнимая единица называются комплексными а- дейсвительная
- 16. z=a+bi Если a=0, то z=bi- чисто мнимое Если b=0, то z=a- действительное Если a=0 и b=0,
- 17. Равенство комплексных чисел Два комплексных числа равны, если равны их действительные части и коэффициенты при мнимой
- 18. Операции над комплексными числами Определим сумму Определим произведение Определим разность
- 19. Свойства операций Коммутативность относительно сложения z1+z2=z2+z1 Ассоциативность относительно сложения (z1+z2)+z3= z1+(z2+z3) Для ∀ z1 ,z2 ∃z:
- 20. Доказательство 3: Для ∀ z1 ,z2 ∃z: z1+z=z2. Число z называют разностью чисел z2и z1 и
- 21. Доказательство 6: Для ∀ z1≠ 0+0i, z2 ∃z: z1 z=z2. Число z называют частным чисел z2и
- 22. Решим систему по формулам Крамера: система имеет единственное решение: откуда:
- 23. Доказательство 7: Дистрибутивность z1ּ(z2+z3)= z1ּz2+z1ּz3 Пусть: тогда
- 24. Сложение и умножение комплексных чисел подчиняется тем же законам, что и сложение и умножение действительных чисел!
- 25. Сопряженные числа Числа a+bi и a-bi называются сопряженными. (отличаются друг от друга только знаками перед мнимой
- 26. Чтобы разделить одно комплексное число на другое, надо числитель и знаменатель домножить на сопряженное знаменателю число
- 27. Решение квадратных уравнений с D Решить квадратное уравнение: Решение: Ответ. Корнями квадратного уравнения с действительными коэффициентами
- 28. ЗАДАНИЕ 1 Дано Найти: Ответ:
- 29. ЗАДАНИЕ 2 Вычислить: Ответ:
- 30. ЗАДАНИЕ 3 По корням составить квадратное уравнение: Ответ:
- 32. Скачать презентацию

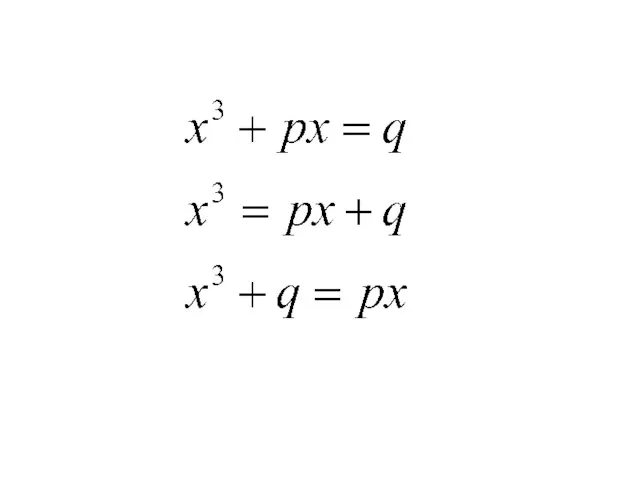



























 Задачи на построение сечений. Урок геометрии в 10 классе
Задачи на построение сечений. Урок геометрии в 10 классе Деление многочлена на двучлен
Деление многочлена на двучлен Внеклассное мероприятие по математике Знатоки против телезрителей
Внеклассное мероприятие по математике Знатоки против телезрителей Табличное сложение и вычитание
Табличное сложение и вычитание Прямоугольник. Площадь прямоугольника
Прямоугольник. Площадь прямоугольника Презентация Один- много
Презентация Один- много Многоугольники. Параллелограмм. Свойства и признаки параллелограмма
Многоугольники. Параллелограмм. Свойства и признаки параллелограмма Статистические данные
Статистические данные Погрешности измерений. Классификация погрешностей
Погрешности измерений. Классификация погрешностей Исследовательская работа по математике: Математика в профессиях наших родителей. 5 класс
Исследовательская работа по математике: Математика в профессиях наших родителей. 5 класс Линейные уравнения Функция. Линейная функция. Математическая викторина
Линейные уравнения Функция. Линейная функция. Математическая викторина Тест по теме: Призма. Часть 2. Вариант 2
Тест по теме: Призма. Часть 2. Вариант 2 Метод построения таблиц сопряженности
Метод построения таблиц сопряженности Площадь трапеции
Площадь трапеции Схемы и графы
Схемы и графы Параллелограмм. Свойства и признаки параллелограмма
Параллелограмм. Свойства и признаки параллелограмма Линейные уравнения с двумя переменными. График линейного уравнения с двумя переменными
Линейные уравнения с двумя переменными. График линейного уравнения с двумя переменными Аксиомы стереометрии
Аксиомы стереометрии Взаимное расположение прямой и плоскости. Признак параллельности прямой и плоскости
Взаимное расположение прямой и плоскости. Признак параллельности прямой и плоскости Решение задач и выражеий
Решение задач и выражеий Симметрия в пространстве
Симметрия в пространстве Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций Единицы времени.
Единицы времени. Интерактивный тренажер Уравнения
Интерактивный тренажер Уравнения Признаки делимости на 10, на 5 и на 2
Признаки делимости на 10, на 5 и на 2 Теория вероятностей. Способность предвидеть возможные варианты будущего
Теория вероятностей. Способность предвидеть возможные варианты будущего Математика әлеміне саяхат
Математика әлеміне саяхат Треугольник и его виды
Треугольник и его виды