Теория вероятностей. Основные понятия презентация

Теория вероятностей
Основные понятия

Этапы развития теории вероятностей
2-я половина XVI века – первые задачи
по теории вероятностей.
Конец XVII- начало XIX века –
формирование как самостоятельной
научной дисциплины.
Конец XIX – конец XX века –
современный этап развития.
Л.Пачоли
Д.Кардано
Н.Тарталья
Б.Паскаль
Я. Бернулли
А.Муавр
П.Лаплас
С.Пуассон
П.Л.Чебышёв
А.А.Марков
А.М.Ляпунов
А.Я.Хинчин
А.Н.Колмогоров

Основные понятия
Стохастический эксперимент
( испытание, опыт) –
- это такой эксперимент, результаты которого заранее нельзя предугадать.
Примеры.
1. Бросание монеты;
2. Выстрел по мишени;
3. Бросание игральной кости (кубика);
4. Измерение физической величины (длины изделия, влажности или температуры, давления)

Случайным называется явление,
которое при неоднократном воспроизведении одного и того же опыта каждый раз может произойти по-иному.
Теория вероятностей - это наука, занимающаяся изучением закономерностей в массовых случайных явлениях.

- это факт, который может произойти или не произойти в результате данного опыта.
Обозначения событий: A, B, C,…,ω,…
Пример 1. Бросание монеты.
Событие А - выпадение герба
Событие B - выпадение цифры
Случайное событие –

Пример 2. Бросание игральной кости
Событие А - выпадение четного числа очков.
Событие В - выпадение числа очков меньше, чем 4.
Событие С - выпадение шести очков.

Вероятность события - это
численная мера объективной возможности появления данного события.
Обозначение: P(A) - вероятность события A

Невозможное и достоверное события
Невозможное событие – событие, которое
не может наступить в данном эксперименте. (Обозначение Ǿ) .
Например, при бросании игральной кости не может выпасть дробное число очков.
Достоверное событие – событие, которое обязательно произойдет в данном эксперименте. ( Ω)
Например, при бросании игральной кости - появление целого числа очков.

Вероятность невозможного события равна 0.
Вероятность достоверного события равна 1.
Вероятность случайного события A:

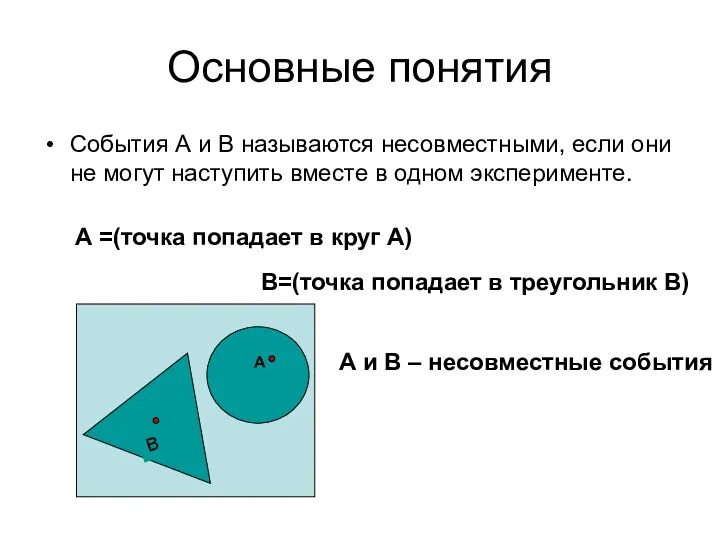
Несовместными называются события, которые не могут произойти одновременно в данном опыте.
Например, при одном бросании игральной кости не могут одновременно выпасть 5 и 6 очков, эти случайные события несовместны.

События называются равновозможными, если
ни одно из них не имеет большой возможности появления, чем другие.
Например, появление герба и появление цифры при бросании монеты.
Например, выпадение одного, двух, трех, четырех, пяти и шести очков при бросании игрального кубика - равновозможные события.

Несколько событий образуют полную группу,
если в результате испытания появится хотя бы одно из них.
Пример: появление одного, двух, трех, четырех, пяти и шести очков при бросании игрального кубика - полная группа событий.

События, несовместные, равновозможные и образующие полную группу, называются случаями или исходами.
Случай называется благоприятствующим данному событию, если появление этого случая влечет за собой появление данного события.
Пример: событию A- появлению четного числа очков при бросании игрального кубика благоприятствуют три случая (исхода) - выпадет 2 очка, 4 очка и 6 очков.

Классическое определение вероятности
Вероятность случайного события A равна отношению числа исходов, благоприятствующих данному событию к общему числу исходов.
n - число всех исходов испытания,
m - число исходов, благоприятствующих событию A.

Примеры
1. Какова вероятность, что при бросании одной монеты выпадет герб?
Событие A -выпадет герб при бросании одной монеты.
Общее число исходов n = 2.
Число исходов, благоприятствующих событию A:
m =1.
Значит

В формуле можно сократить на .
Тогда получится
Пример:
Если , то проще использовать формулу

Пример
Нужно выбрать в подарок 4 из имеющихся 10-ти разных книг. Сколькими способами это можно сделать?

Размещениями из n элементов по m называются
комбинации (группы, наборы), составленные из этих n элементов по m в каждой, отличающиеся либо самими элементами, либо их порядком.
Число размещений:

Число размещений из n элементов по m
Можно сократить на
Пример:

Пример 1
В приборе имеется 11 деталей, из них 3 неисправных. Случайным образом выбирают 5 деталей. Какова вероятность, что среди проверенных деталей окажутся неисправными 2 детали?
Решение: Вычислим общее количество комбинаций из 11 деталей по 5 деталей: , а количество благоприятных случаев равно . Действительно, ,
где - количество способов выбрать из 8 исправных деталей 3 детали, а - количество способов выбрать из 3 неисправных деталей 2 детали. Имеем:
, . Т.е. получим

Статистическое определение вероятности
Пусть n – число повторений одного и того же стохастического эксперимента.
m(A) – число наступлений события А.
Проводятся различные серии из n повторений одного и того же стохастического эксперимента при
Определение.
Событие А называется стохастически устойчивым,
если
В этом случае Р(А)=р - это статистическое определение вероятности.

Частота события
Пример. Бросание монеты.
А=(выпадение герба).
Бюффон (XVII век). n=4040, m(A)=2048.
К.Пирсон (конец XIX века). n=24000, m(A)=12012.
P(A)=0,5

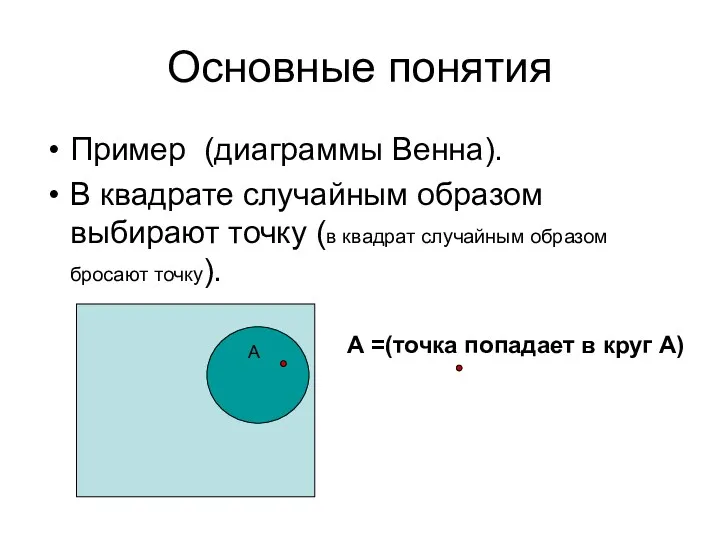
Геометрическое определение вероятности
Пример.
В квадрате случайным образом выбирают точку (в квадрат случайным образом бросают точку).
А =(точка попадает в круг А)

Геометрическое определение вероятности (продолжение)
На фигуре Ф случайным образом выбирают точку (любое положение точки равновозможно).
А=(точка попадает в область А).
Ф
А

Пример.
На отрезок длины L наугад бросается точка. Какова вероятность того, что она упадет не дальше, чем на расстоянии m от середины отрезка.
Решение.
Событие
L
А: точка упадет не далее, чем на расстоянии m от середины,
т.е. точка попадает на отрезок длины 2m

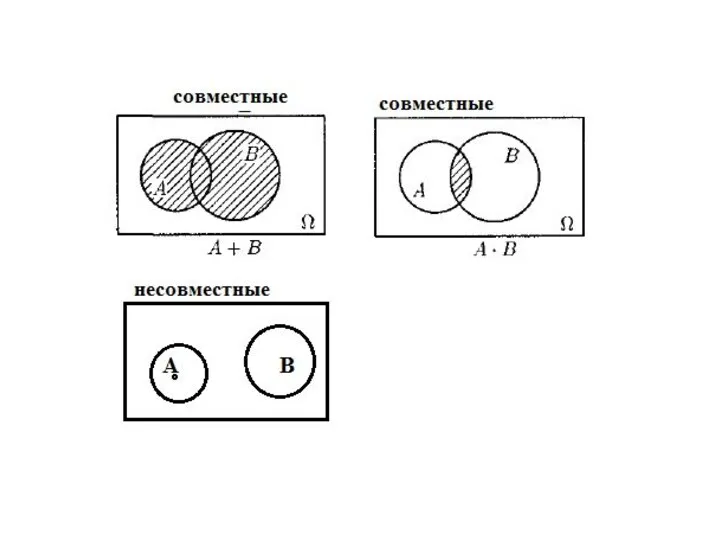
Сложение и умножение событий
Сумма двух событий А и В – это такое событие С=А+В, которое происходит, когда наступает хотя бы одно из событий А или В.
Произведение двух событий А и В – это такое событие С=АВ, которое происходит, когда наступают и А и В вместе.
Пример. Два стрелка делают по одному выстрелу в мишень. Событие A - попадет первый, событие B - попадет второй.
A+B - попадет хотя бы один, т.е. или первый или второй
или оба вместе.
- попадут оба (первый и второй).

Основные понятия
Пример (диаграммы Венна).
В квадрате случайным образом выбирают точку (в квадрат случайным образом бросают точку).
А =(точка попадает в круг А)

Основные понятия
В=(точка попадает в треугольник В)
А
А+В=(точка попадает хотя бы в одну фигуру А и В).

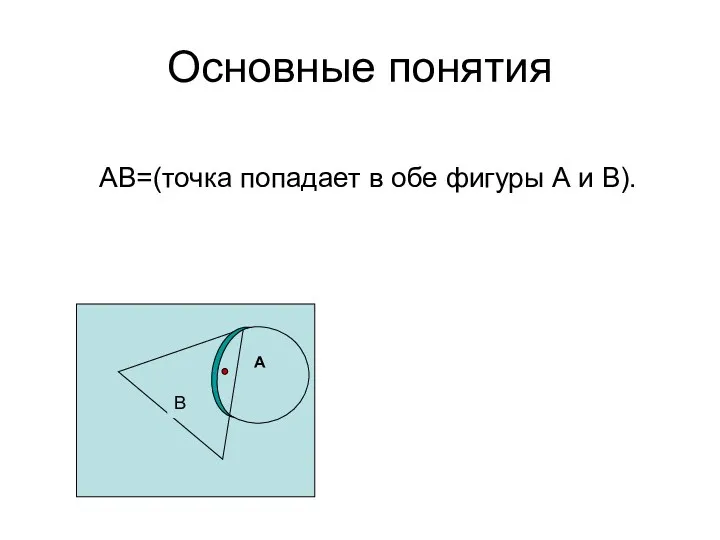
Основные понятия
A
АВ=(точка попадает в обе фигуры А и В).

Основные понятия
События А и В называются несовместными, если они не могут наступить вместе в одном эксперименте.
А =(точка попадает в круг А)
В=(точка попадает в треугольник В)
А и В – несовместные события

Основные теоремы теории вероятностей
1. Теорема сложения вероятностей для несовместных событий
Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий
Доказательство.
Пусть n – число всех исходов испытания,
- число исходов, благоприятствующих событию А,
- число исходов, благоприятствующих событию В,
тогда поскольку события A и B несовместны, событию A+B, т.е. наступлению или A или B будет благоприятствовать исходов, т.к. у событий A и B нет общих благоприятствующих исходов.

Пример
В лотерее 1000 билетов. Из них 1 билет - выигрыш 100 тыс. рублей, 50 билетов по 5 тыс. рублей и 100 билетов по 1 тыс. рублей. Какова вероятность выиграть по одному билету не менее 5 тыс. рублей?
Решение. Событие C - выиграть по одному билету не менее 5 тыс. рублей.
A - выиграть 100 тыс. рублей, B - выиграть 5 тыс. рублей.
События A и B несовместны.
C = A + B

Зависимые и независимые случайные события
Два события называются независимыми, если вероятность появления одного не зависит от того, произошло второе или нет.
Пример. Два стрелка делают по одному выстрелу в мишень. Событие A - попадет первый, событие B - попадет второй. A и B - независимые события.
Два события называются зависимыми, если вероятность появления одного зависит от того, произошло второе или нет.
Пример. В ящике имеется 20 шаров, из них 12 белых и 8 красных. Из ящика берут наугад один шар и откладывают его в сторону. Событие A- этот шар белый. Затем берут еще один шар. Событие B - второй шар красный. Эти два события A и B зависимые.
1. Пусть событие A произошло, тогда в ящике осталось 11 белых и 8 красных шаров. Вероятность события B при условии, что событие A произошло обозначается так: или так .

Умножение вероятностей
Вероятность произведения двух независимых
событий равна произведению их вероятностей.

2. Теорема сложения вероятностей для совместных событий
Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.
Доказательство.
Пусть n – число всех исходов испытания,
- число исходов, благоприятствующих событию А,
- число исходов, благоприятствующих событию В,
По условию события A и B совместны, значит у них есть общие благоприятствующие исходы, обозначим число этих исходов .
Число исходов, благоприятствующих событию A+B, будет
, т.к. в сумму исходы, благоприятствующие совместному появлению A и B входят дважды. Тогда

Пример
Два стрелка делают по одному выстрелу в мишень. Вероятность попадания первого равна 0,8, а второго - 0,7. Найти вероятность того, что мишень будет поражена, т.е. что попадет хотя бы один стрелок.
Решение. Пусть событие C - попадет хотя бы один стрелок,
C = A + B.
Событие A - попадет первый, P(A) = 0,8,
событие B - попадет второй, P(B) = 0,7.
A и B совместны ( могут произойти вместе) . Тогда

Для случая суммы трех совместных событий:
Еще более громоздкой будет формула для вероятности суммы четырех совместных событий.
Есть более рациональный способ вычисления - это переход к противоположному событию (рассмотрим на следующих слайдах).

Противоположные события
Два несовместных события, образующих полную группу, называются противоположными.
Они обозначаются A и .
, - достоверное событие.
Пример. A - попадание в цель, P(A) = 0,9
- промах, .

То есть событию: хотя бы один противоположно событие: ни один.
Если нужно найти вероятность суммы трех или более совместных событий, то более рациональным решением будет переход к противоположному событию, как в предыдущем примере.

2). Брошены монета и игральный кубик. Какова вероятность, что выпадет герб и шесть очков?
Ответ:
3). В студии телевидения 3 телекамеры.
Для каждой камеры вероятность того, что она включена в данный момент, равна 0,6. Найти вероятность того, что в данный момент включена хотя бы одна камера.

Решение.
А – включена первая телекамера,
В – включена вторая телекамера,
С – включена третья телекамера, A, B, C - совместные события
D – включена хотя бы одна телекамера, D = A + B + C
- все телекамеры выключены (это событие противоположное D).
Тогда и

Примеры.
1). Определить надежность (вероятность безотказной работы за время Т) схемы, составленной из двух последовательно соединенных элементов А и В, если надежность этих элементов соответственно равна