Содержание
- 2. Тройные интегралы
- 3. Определение тройного интеграла. Рассмотрим тело, занимающее пространственную область Т, и предположим, что плотность распределения массы в
- 4. , где f(x,y,z) – любая функция, непрерывная в замкнутой ограниченной области Т, имеющей объем V. Обычно
- 5. Вычисление тройных интегралов. Декартовы прямоугольные координаты Пусть дан тройной интеграл от функции f(x,y,z) . Область Т
- 6. Опишем около Т цилиндрическую поверхность с образующей, перпендикулярной к плоскости ОХУ. Она касается области Т вдоль
- 7. Сначала интегрируем по направлению оси Z. Для этого функция f( x ,y , z) интегрируется по
- 8. Получим значение искомого тройного интеграла, если возьмем интеграл от функции F( x ,y) при условии, что
- 9. Таким образом, вычисление тройного интеграла по области T производится посредством трех последовательных интегрирований.
- 10. Если областью интегрирования служит внутренняя часть параллелепипеда с гранями параллельными координатным плоскостям, то пределы интегрирования постоянные
- 11. Пример. Вычислить где Т – область, ограниченная координатными плоскостями x=0, y=0, z=0 и плоскостью x +
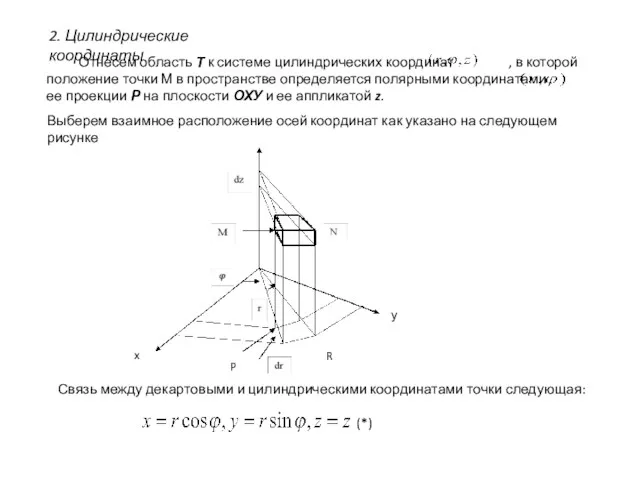
- 12. 2. Цилиндрические координаты Отнесем область Т к системе цилиндрических координат , в которой положение точки М
- 13. Частичные области Vi - прямые цилиндры MN. Так как объем цилиндра MN равен площади основания, умноженной
- 14. Получаем В обычно встречающихся случаях область можно не строить и расставлять пределы интегрирования прямо по виду
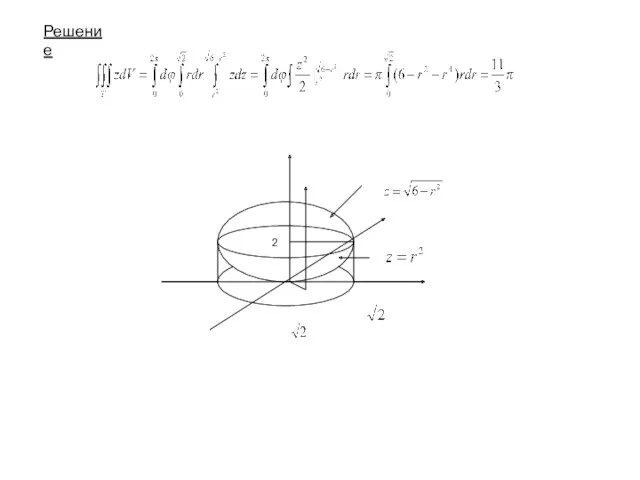
- 15. Пример Вычислить интеграл , где область Т ограничена снизу параболоидом а сверху сферой . Уравнения этих
- 16. Решение
- 17. 3. Сферические координаты Отнесем область интегрирования Т к сферическим координатам В этой системе координат положение точки
- 18. Разобьем область Т на частичные области тремя системами координатных поверхностей: которыми будут соответственно сферы с центром
- 19. Заменив в тройном интеграле x, y, z по формулам (*) и взяв элемент объема равным (**),
- 21. Скачать презентацию
















 Обобщающий урок по теме параллелограмм 8 класс
Обобщающий урок по теме параллелограмм 8 класс Тетраэдр. Сечение тетраэдра
Тетраэдр. Сечение тетраэдра Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Решение СЛАУ методом Гаусса
Решение СЛАУ методом Гаусса Презентация по математике по теме Логарифм для 10-11 класса
Презентация по математике по теме Логарифм для 10-11 класса Обчислення на основі нумерації. Складання задач різних типів за малюнками та частиною умови. Урок №111
Обчислення на основі нумерації. Складання задач різних типів за малюнками та частиною умови. Урок №111 Умножение положительных и отрицательных чисел
Умножение положительных и отрицательных чисел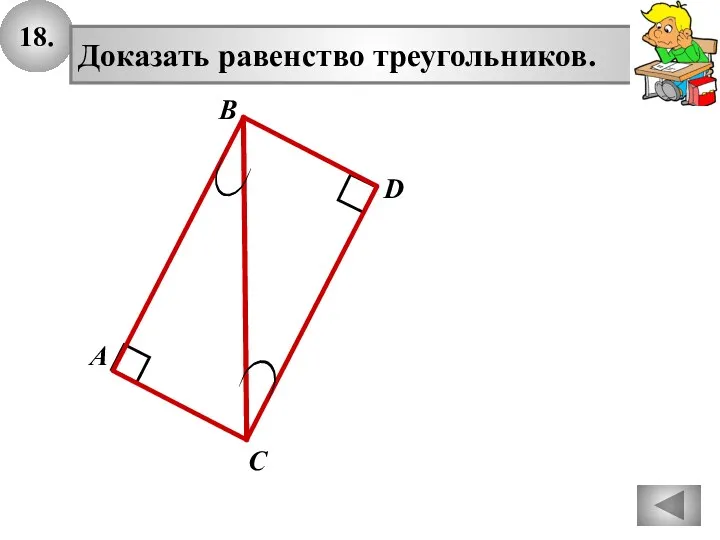 Прямоугольные треугольники
Прямоугольные треугольники Что такое умножение
Что такое умножение Числа и вычисления. Подготовка к ГИА. К уроку математики в 9 классе
Числа и вычисления. Подготовка к ГИА. К уроку математики в 9 классе Выражения, равенства, неравенства, уравнения .
Выражения, равенства, неравенства, уравнения . Основы математической обработки информации. Вариационные ряды и их характеристики. (Лекция 1)
Основы математической обработки информации. Вариационные ряды и их характеристики. (Лекция 1) Дифференциальное исчисление функций нескольких переменных
Дифференциальное исчисление функций нескольких переменных Сумма и разность дробей
Сумма и разность дробей Математические модели
Математические модели Длина окружности и площадь круга
Длина окружности и площадь круга Логарифмическая функция, ее график и свойства
Логарифмическая функция, ее график и свойства Разложение на множители суммы и разности кубов
Разложение на множители суммы и разности кубов Метрические задачи
Метрические задачи Основные сведения теории вероятностей. Надежность технических систем и техногенный риск
Основные сведения теории вероятностей. Надежность технических систем и техногенный риск Сложение однозначных чисел с переходом через десяток вида + 8, +9
Сложение однозначных чисел с переходом через десяток вида + 8, +9 Решение системы способом подстановки. 7 класс
Решение системы способом подстановки. 7 класс Решение систем линейных уравнений. 7 класс
Решение систем линейных уравнений. 7 класс Презентация Метр 2 класс
Презентация Метр 2 класс Графический метод решения уравн
Графический метод решения уравн Вычислительная математика. Лекция 5. Системы линейных алгебраических уравнений
Вычислительная математика. Лекция 5. Системы линейных алгебраических уравнений Сложение и вычитание алгебраических дробей с разными знаменателями. 7 класс
Сложение и вычитание алгебраических дробей с разными знаменателями. 7 класс Презентация Устный счёт 2 класс 1 четверть № 3
Презентация Устный счёт 2 класс 1 четверть № 3