Содержание
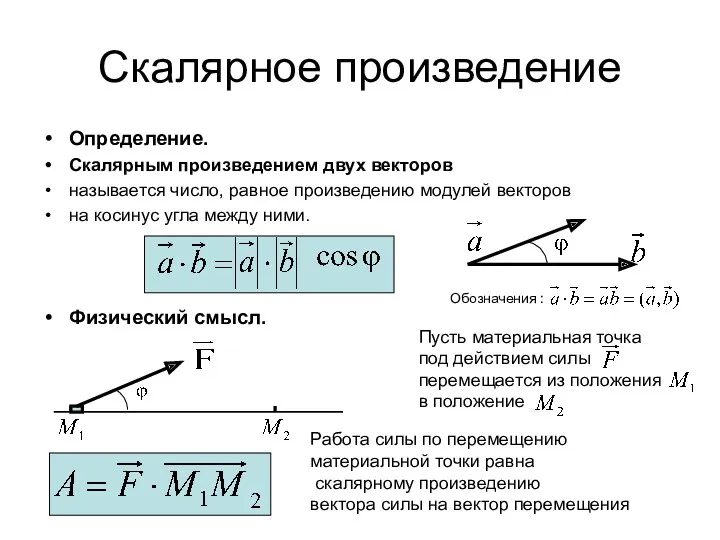
- 2. Скалярное произведение Определение. Скалярным произведением двух векторов называется число, равное произведению модулей векторов на косинус угла
- 3. Свойства скалярного произведения. 1. - переместительный закон 2. - сочетательный закон 3.
- 4. Доказательство свойства № 3. так как по третьему свойству проекций Аналогично можно записать . Следствие
- 5. 4. - распределительный закон Доказательство свойства № 4.
- 6. Свойства скалярного произведения (продолжение) 5. 6. так как Скалярный квадрат вектора равен квадрату его модуля. 7.
- 7. Доказательство. Необходимость: если то , значит Достаточность: если , то и
- 8. Пример. Найти модуль вектора , если и угол между векторами Решение. Находим скалярный квадрат вектора :
- 9. Так как орты перпендикулярны, то их скалярное произведение равно нулю: аналогично, Скалярные квадраты ортов : Скалярное
- 10. Скалярное произведение векторов, заданных в координатной форме. Пусть Тогда Скалярное произведение векторов равно сумме произведений соответствующих
- 11. Доказательство. Дано: или Вычислим их скалярное произведение Воспользуемся распределительным и сочетательным свойствами скалярного произведения (свойством 4
- 12. Все остальные скалярные произведения базисных векторов равны нулю, т.к. являются скалярными произведениями перпендикулярных векторов (свойство 7).
- 13. В частности, Правило вычисления длины вектора. Длина вектора равна квадратному корню из суммы квадратов координат этого
- 14. Условие перпендикулярности векторов в координатной форме : Условие перпендикулярности векторов в координатной форме :
- 15. Пример. Задачи
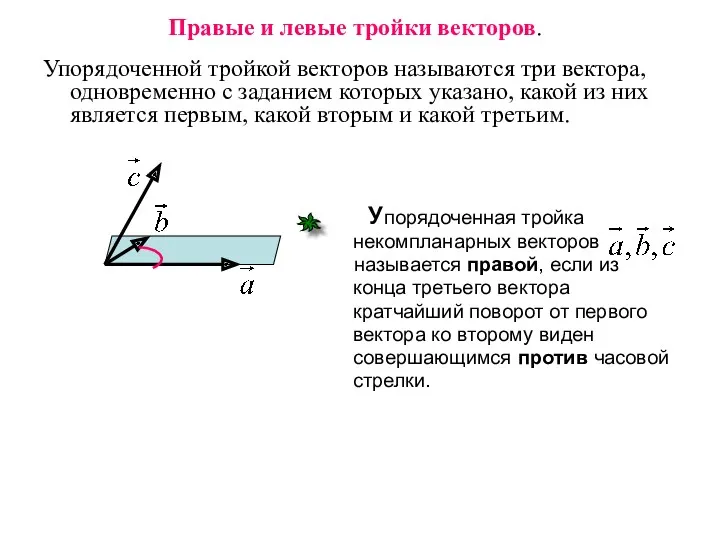
- 16. Правые и левые тройки векторов. Упорядоченной тройкой векторов называются три вектора, одновременно с заданием которых указано,
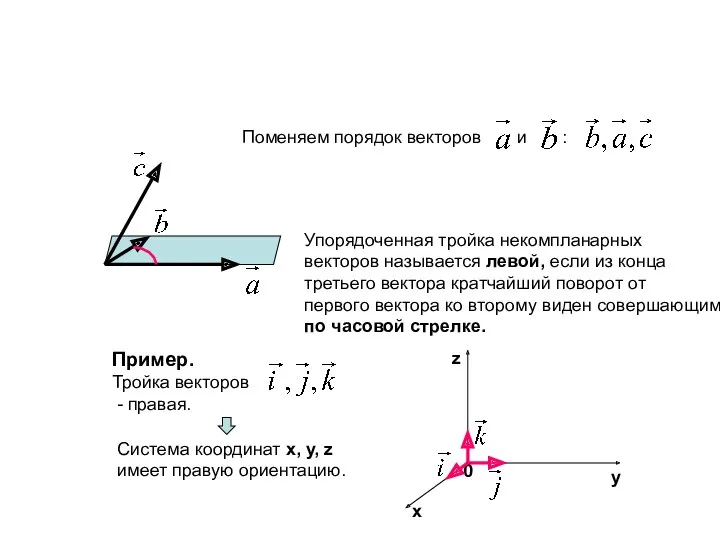
- 17. Векторное произведение Поменяем порядок векторов и : Упорядоченная тройка некомпланарных векторов называется левой, если из конца
- 18. Векторное произведение Векторным произведением двух векторов называется третий вектор , удовлетворяющий трем условиям : 1. 2.
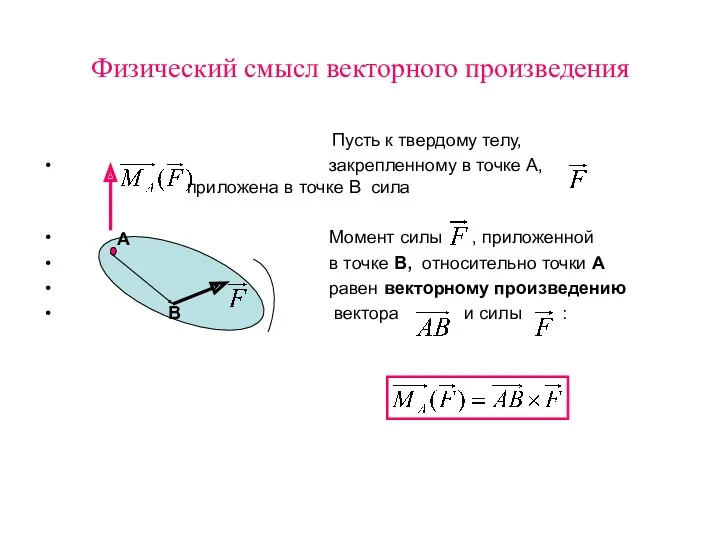
- 19. Физический смысл векторного произведения Пусть к твердому телу, закрепленному в точке А, приложена в точке В
- 20. Векторное произведение Свойства векторного произведения. 1. 2. 3. 4. Геометрический смысл . Модуль векторного произведения двух
- 21. 5. Необходимое и достаточное условие коллинеарности двух векторов. Два ненулевых вектора коллинеарны тогда и только тогда,
- 23. Векторное произведение ортов Найдем векторное произведение ортов координатных осей. Докажем, что а) б) векторы образуют правую
- 24. Векторное произведение Векторное произведение векторов, заданных в координатной форме. Пусть Тогда
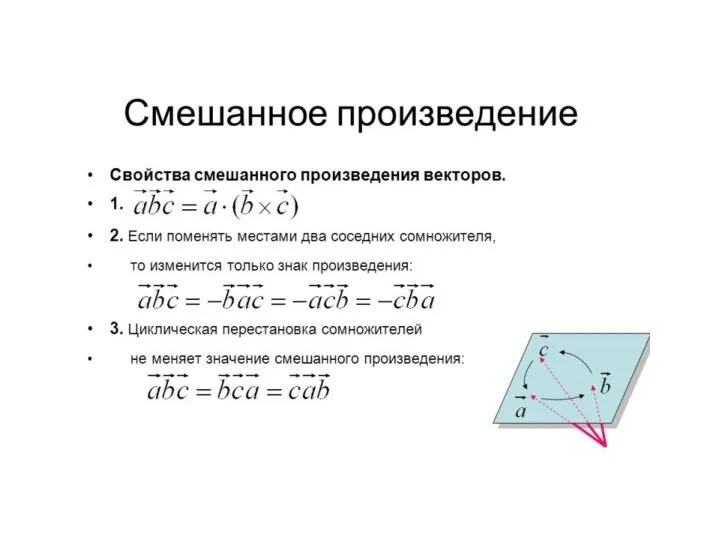
- 26. Смешанное произведение Определение. Смешанным произведением трех векторов называется векторное произведение первых двух векторов, умноженное скалярно на
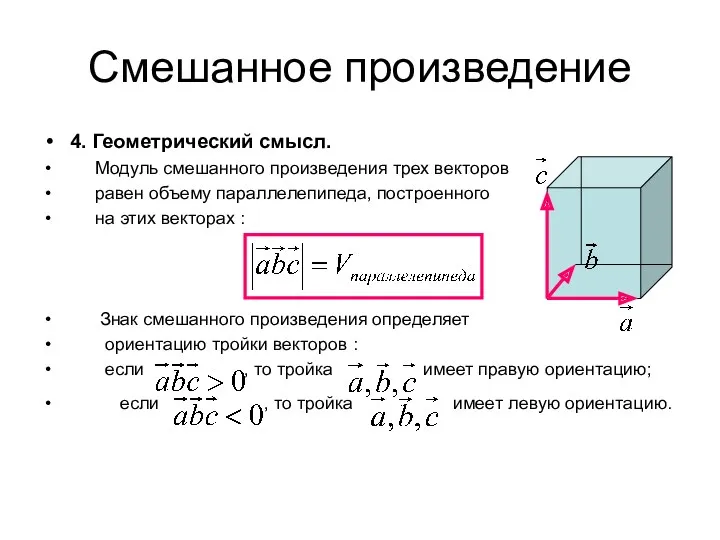
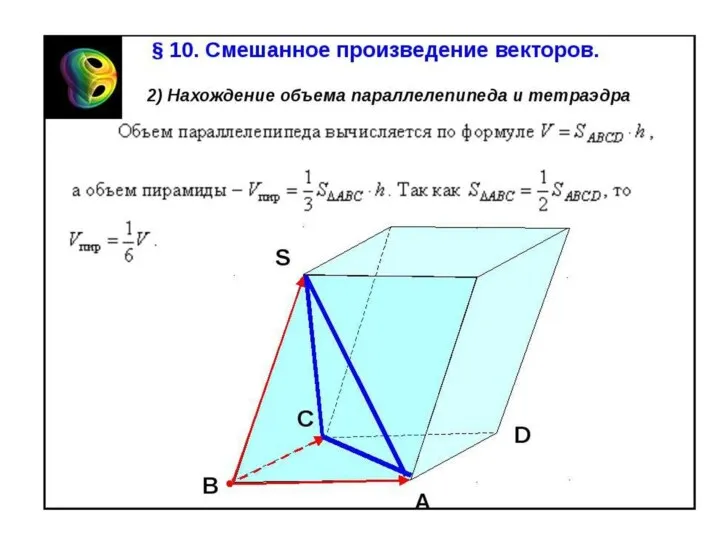
- 28. Смешанное произведение 4. Геометрический смысл. Модуль смешанного произведения трех векторов равен объему параллелепипеда, построенного на этих
- 29. Смешанное произведение 5. Необходимое и достаточное условие компланарности трех векторов. Три ненулевых вектора компланарны тогда и
- 33. Скачать презентацию























 Геометрические построения. Деление окружности
Геометрические построения. Деление окружности Получение схемы логического элемента по итоговым значениям логической функции с использованием СДНФ ИЛИ СКНФ
Получение схемы логического элемента по итоговым значениям логической функции с использованием СДНФ ИЛИ СКНФ 01-Формула суммы п первых членов арифметической прогрессии
01-Формула суммы п первых членов арифметической прогрессии Счёт в пределах 10
Счёт в пределах 10 Проектируем сад
Проектируем сад Производная функции
Производная функции Таблица сложения чисел с переходом через десяток
Таблица сложения чисел с переходом через десяток Пропорции» и «Прямая и обратная пропорциональность
Пропорции» и «Прямая и обратная пропорциональность Определители. Вспомогательные определения
Определители. Вспомогательные определения Математика в профессиях
Математика в профессиях Relational algebra. Lecture 8
Relational algebra. Lecture 8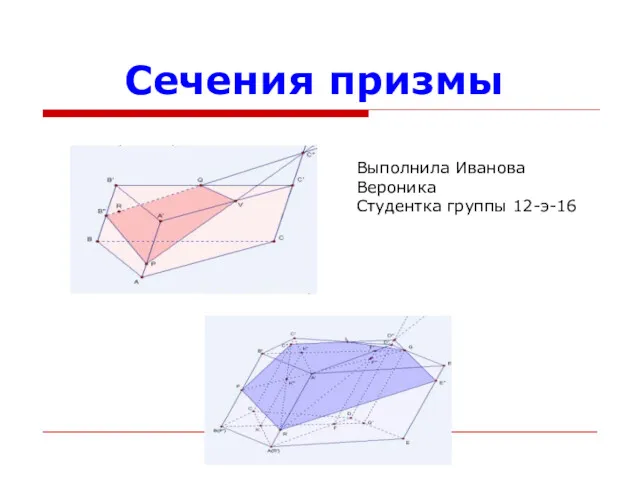 Сечения призмы
Сечения призмы Час занимательной математики Заниматика
Час занимательной математики Заниматика Обходы графов
Обходы графов Пьер Ферма (1601-1665)
Пьер Ферма (1601-1665) Компьютерный практикум по математическому анализу в среде Matlab. Практическое занятие 5
Компьютерный практикум по математическому анализу в среде Matlab. Практическое занятие 5 Таблица умножения и деления на 2
Таблица умножения и деления на 2 презентация по математике
презентация по математике Статистика рынка труда
Статистика рынка труда Модуль числа. 6 класс
Модуль числа. 6 класс Математика для малышей
Математика для малышей Задачи с экономическим содержанием
Задачи с экономическим содержанием Четные и нечетные функции
Четные и нечетные функции Статистика. Основные этапы статистического анализа
Статистика. Основные этапы статистического анализа Квадратный корень. Арифметический квадратный корень
Квадратный корень. Арифметический квадратный корень 4 класс. Табличные случаи умножения и деления. Урок - путешествие В цирк
4 класс. Табличные случаи умножения и деления. Урок - путешествие В цирк Площадь треугольника
Площадь треугольника Тренажёр по математике 1класс
Тренажёр по математике 1класс