Содержание
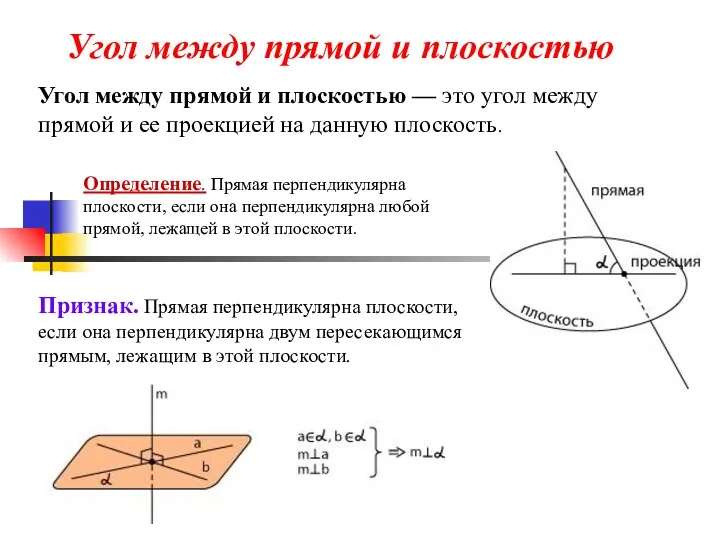
- 2. Угол между прямой и плоскостью Угол между прямой и плоскостью — это угол между прямой и
- 3. Пример В правильной треугольной пирамиде с основанием известны ребра , Найдите угол, образованный плоскостью основания и
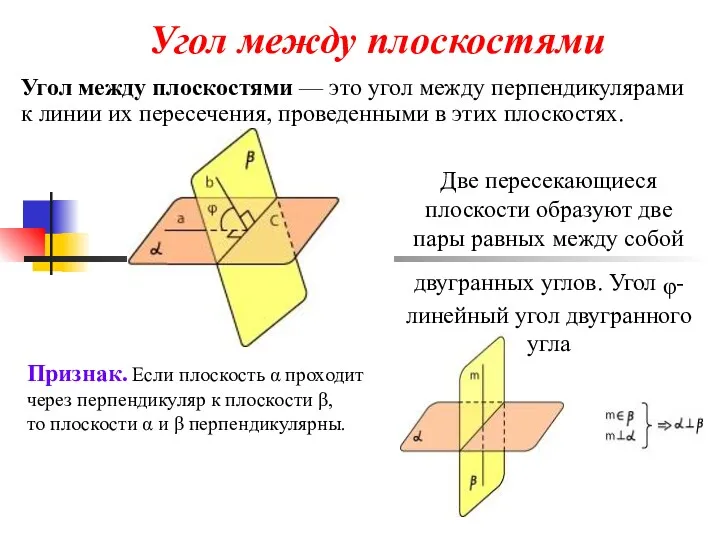
- 4. Угол между плоскостями Угол между плоскостями — это угол между перпендикулярами к линии их пересечения, проведенными
- 5. Пример. Дан прямоугольный параллелепипед АВСDA1B1C1D1, в котором АВ=3, AD=2, АА1=7 и точка E делит сторону АА1
- 6. По теореме Пифагора из треугольника АВF находим : Длину АМ найдем через площади треугольника АBF: 1)
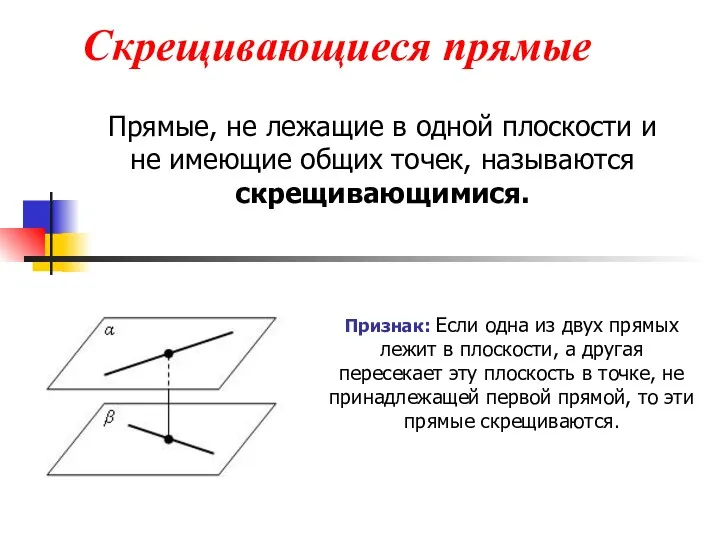
- 7. Скрещивающиеся прямые Прямые, не лежащие в одной плоскости и не имеющие общих точек, называются скрещивающимися. Признак:
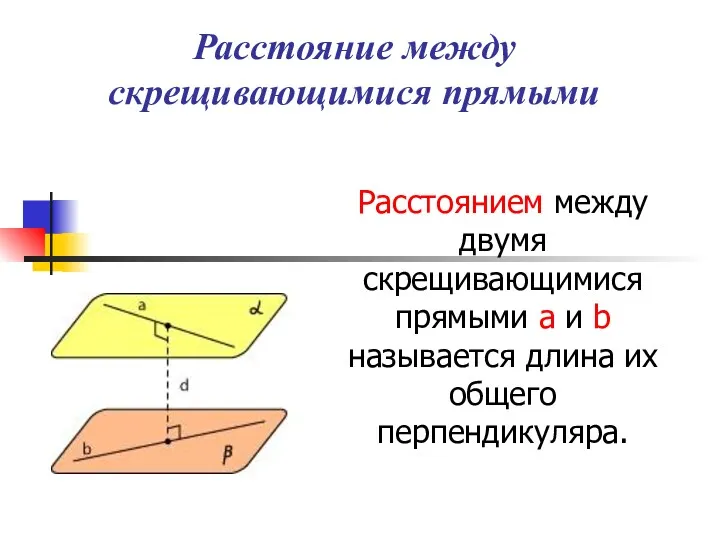
- 8. Расстояние между скрещивающимися прямыми Расстоянием между двумя скрещивающимися прямыми а и b называется длина их общего
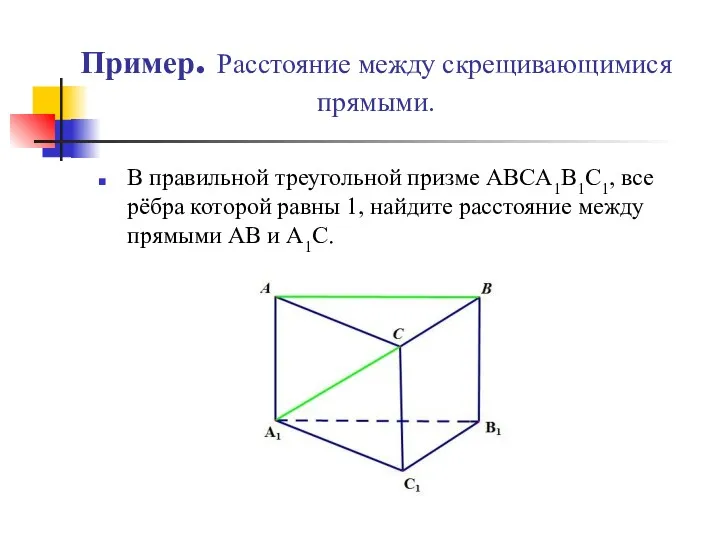
- 9. Пример. Расстояние между скрещивающимися прямыми. В правильной треугольной призме ABCA1B1C1, все рёбра которой равны 1, найдите
- 10. Решение: (Гиперссылки\3.docx)
- 11. Угол между скрещивающимися прямыми За величину угла между скрещивающимися прямыми a и b принимается величина угла
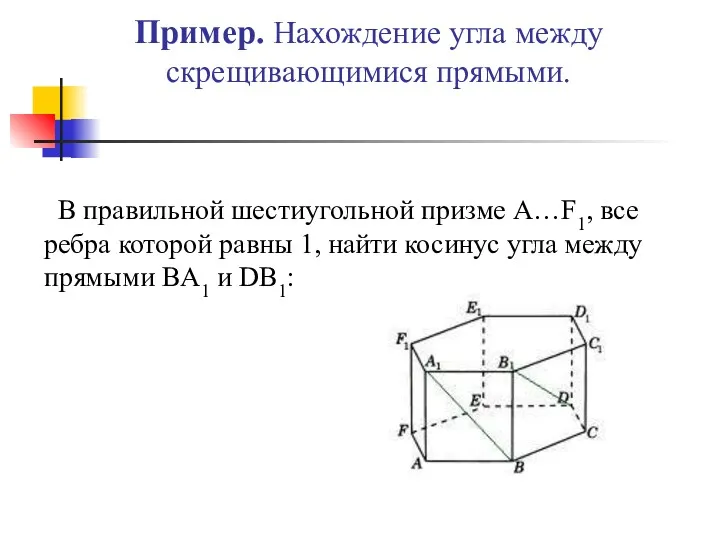
- 12. Пример. Нахождение угла между скрещивающимися прямыми. В правильной шестиугольной призме A…F1, все ребра которой равны 1,
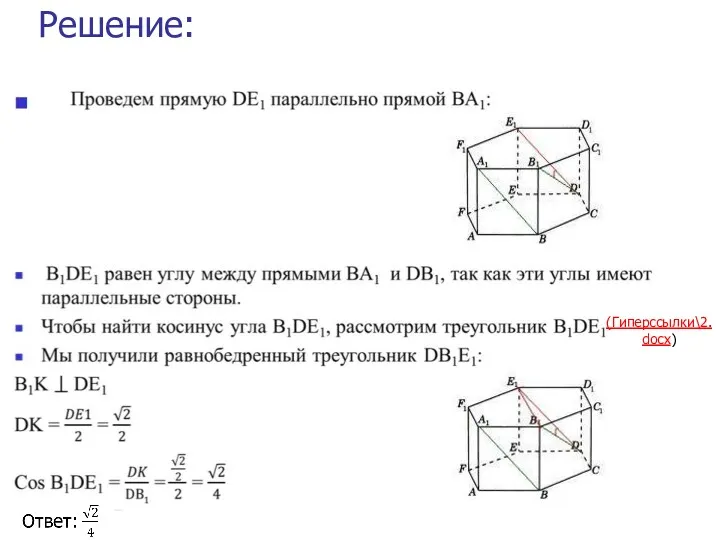
- 13. Решение: (Гиперссылки\2.docx)
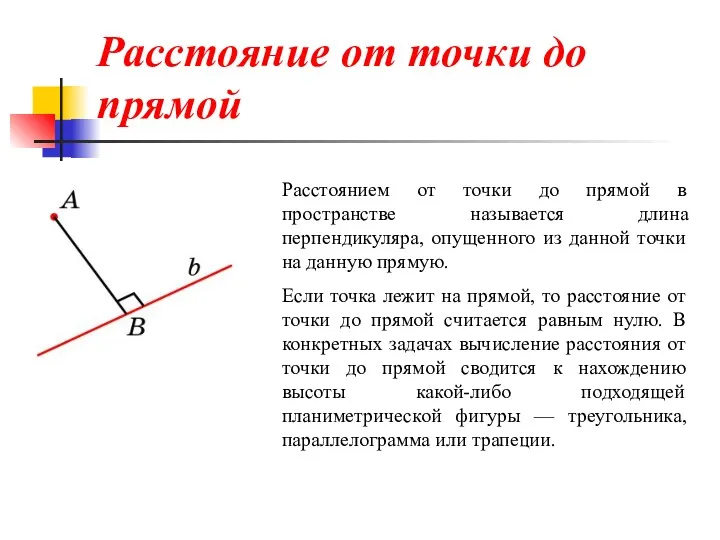
- 14. Расстоянием от точки до прямой в пространстве называется длина перпендикуляра, опущенного из данной точки на данную
- 15. Нахождение расстояний 1 Для нахождения расстояния от точки A до прямой l перпендикуляр AH, опущенный из
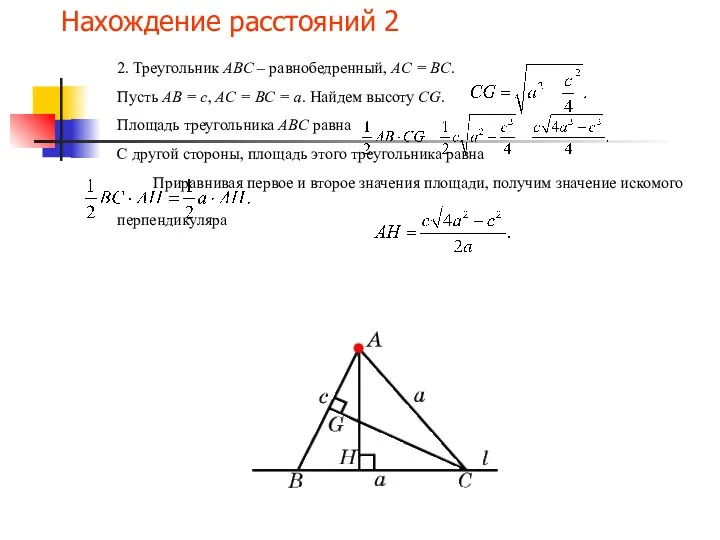
- 16. Нахождение расстояний 2 2. Треугольник ABC – равнобедренный, AC = BC. Пусть AB = c, AC
- 17. Нахождение расстояний 3 3. Треугольник ABC – прямоугольный, угол A – прямой. Пусть AB = c,
- 18. Нахождение расстояний 4 4. Треугольник ABC – произвольный. Пусть AB = c, AC = b, BC
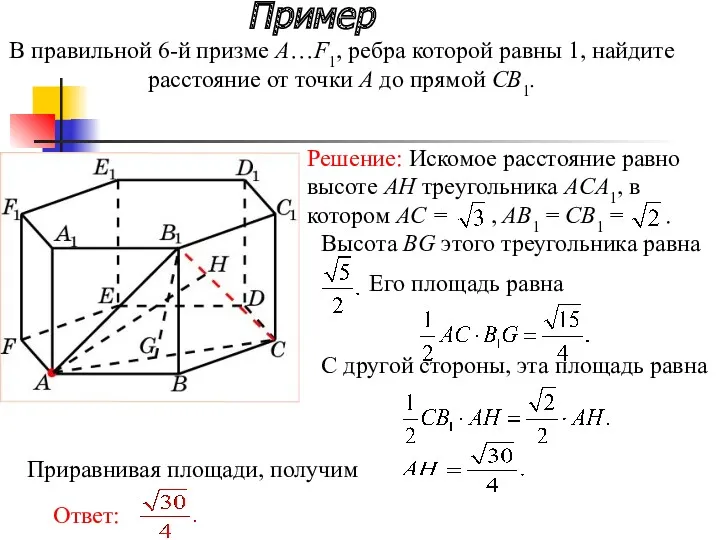
- 19. В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние от точки A до прямой
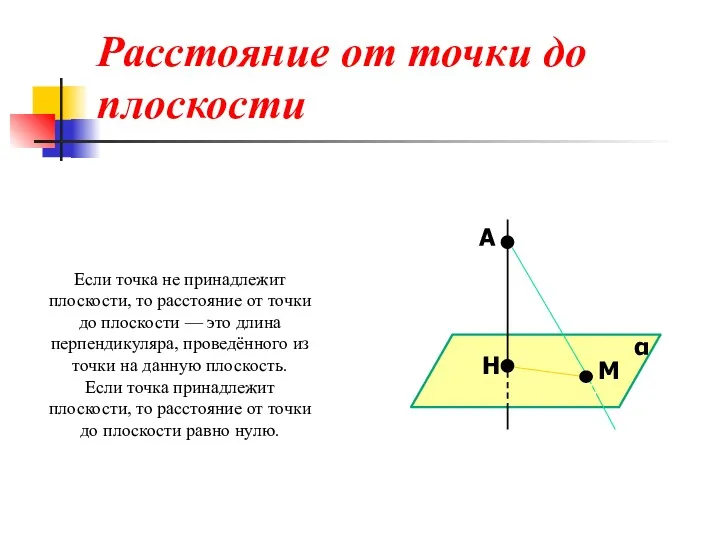
- 20. А Н М α Расстояние от точки до плоскости Если точка не принадлежит плоскости, то расстояние
- 21. Расстояние от точки до плоскости Методы Поэтапно-вычислительный метод Метод параллельных прямых и плоскостей Векторный метод Координатный
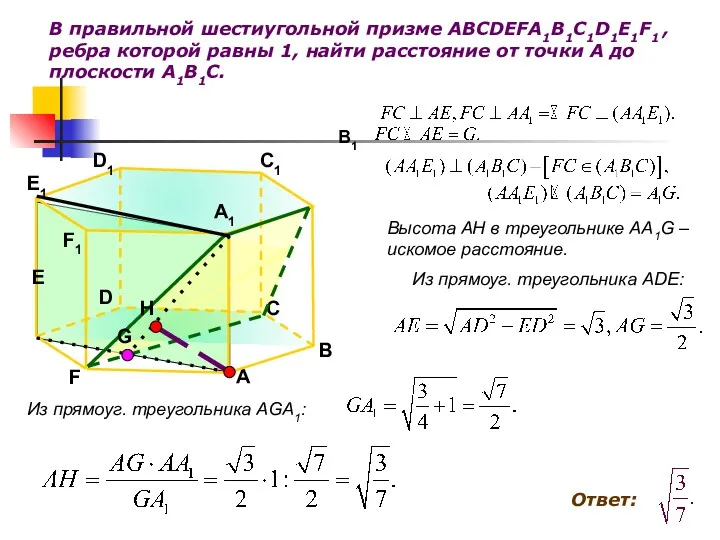
- 22. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , ребра которой равны 1, найти расстояние от точки А до
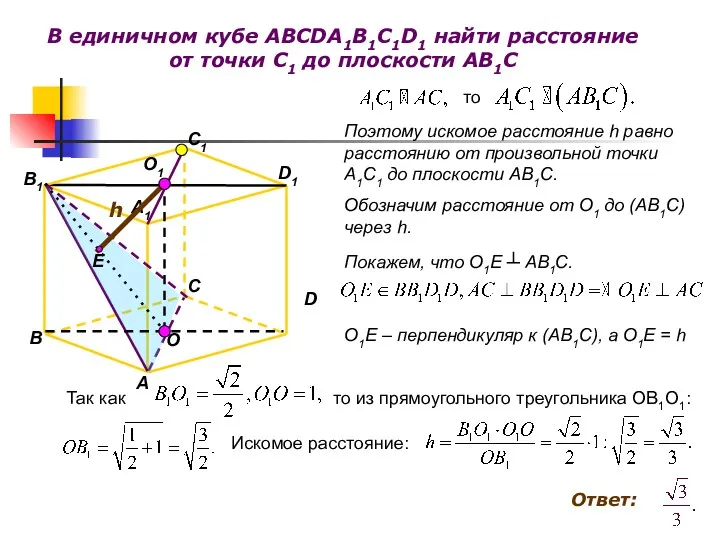
- 23. В единичном кубе ABCDA1B1C1D1 найти расстояние от точки C1 до плоскости AB1C B D C A
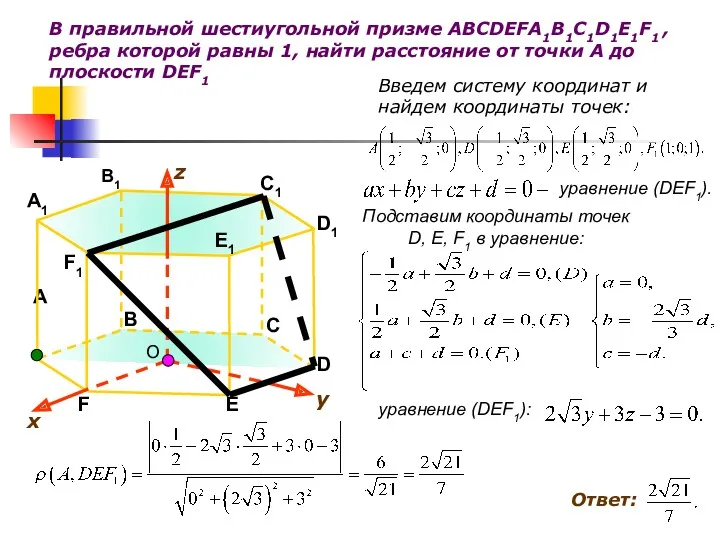
- 24. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , ребра которой равны 1, найти расстояние от точки А до
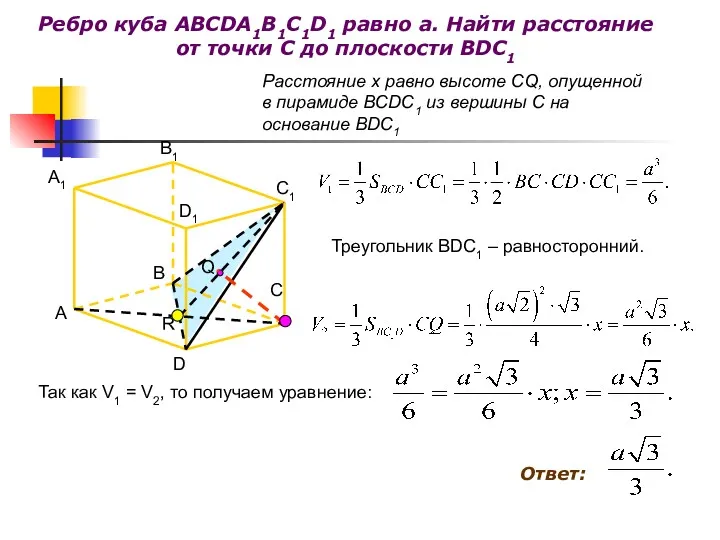
- 25. Ребро куба ABCDA1B1C1D1 равно а. Найти расстояние от точки C до плоскости BDC1 D C B
- 26. Метод координат
- 27. Главные формулы Косинус угла φ между векторами a = (x1; y1; z1) и b = (x2;
- 28. Итак, пусть отрезок задан своими концами — точками A = (xa; ya; za) и B =
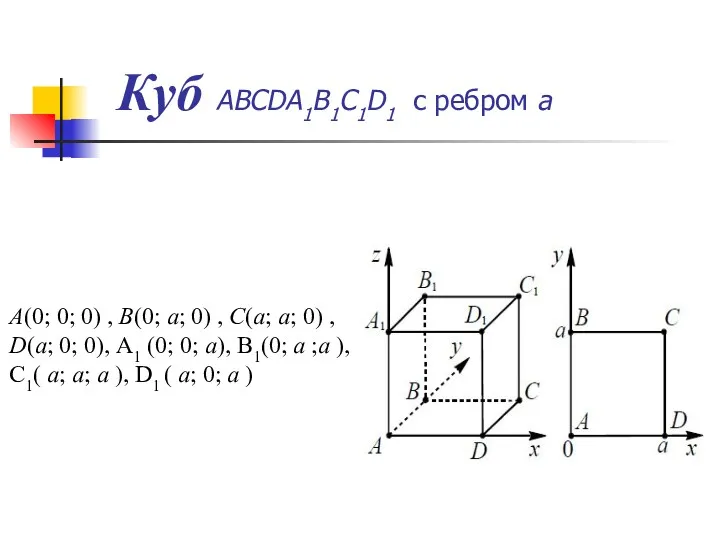
- 29. Куб ABCDA1B1C1D1 с ребром a A(0; 0; 0) , B(0; a; 0) , C(a; a; 0)
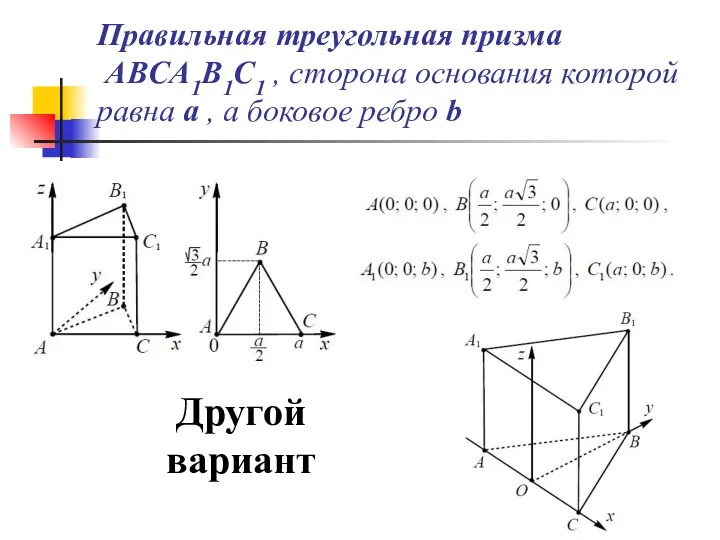
- 30. Правильная треугольная призма ABCA1B1C1 , сторона основания которой равна a , а боковое ребро b Другой
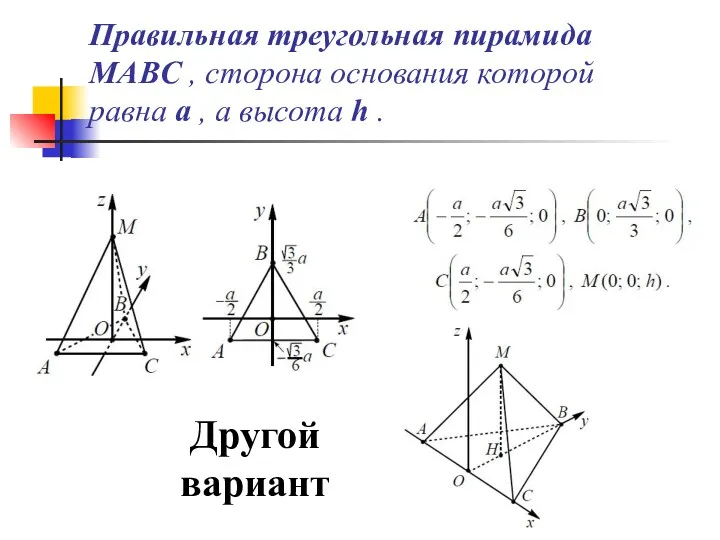
- 31. Правильная треугольная пирамида MABC , сторона основания которой равна a , а высота h . Другой
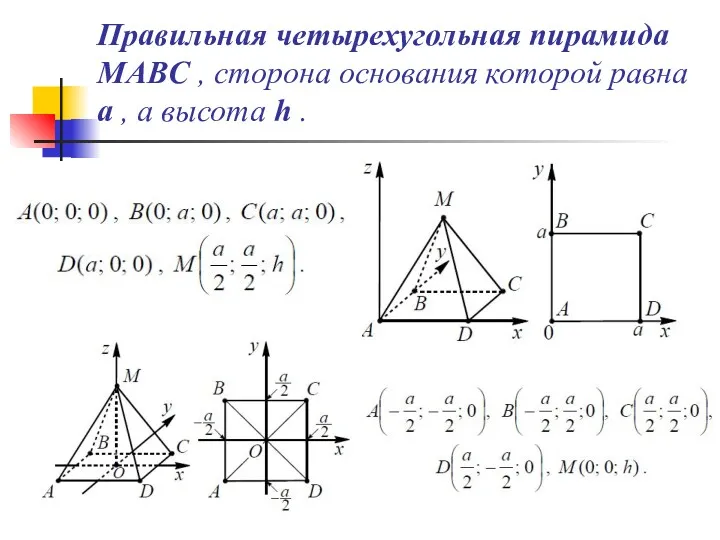
- 32. Правильная четырехугольная пирамида MABC , сторона основания которой равна a , а высота h .
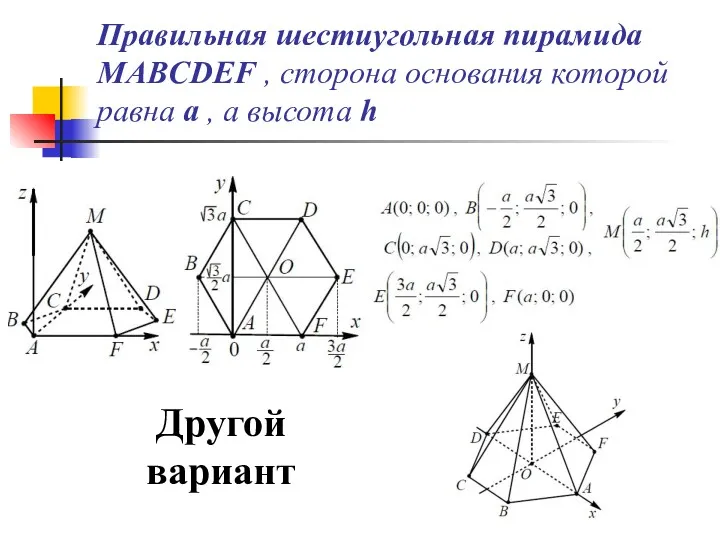
- 33. Правильная шестиугольная пирамида MABCDEF , сторона основания которой равна a , а высота h Другой вариант
- 34. Пример Пример
- 35. Пример 2. Точка E — середина ребра CC1 куба ABCDA1B1C1D1. Найдите угол между прямыми BE и
- 36. Сечения
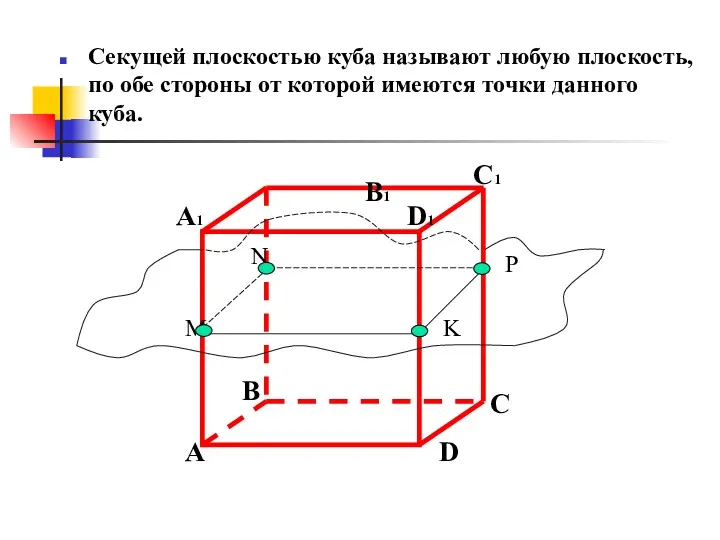
- 37. Секущей плоскостью куба называют любую плоскость, по обе стороны от которой имеются точки данного куба. A
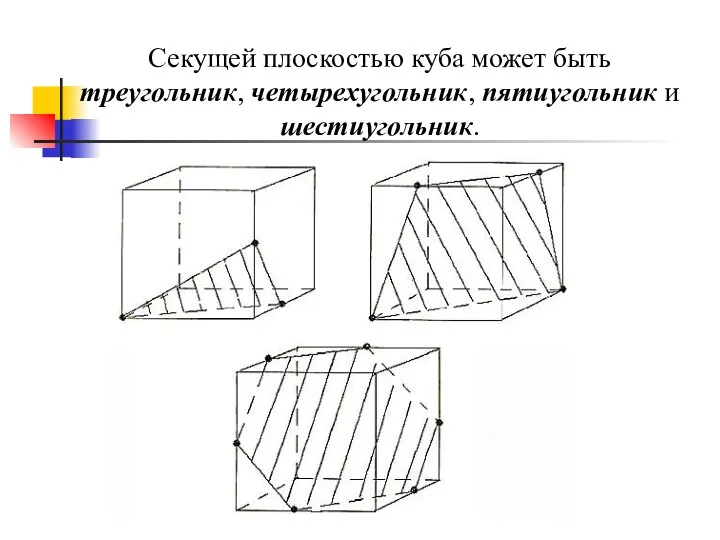
- 38. Секущей плоскостью куба может быть треугольник, четырехугольник, пятиугольник и шестиугольник.
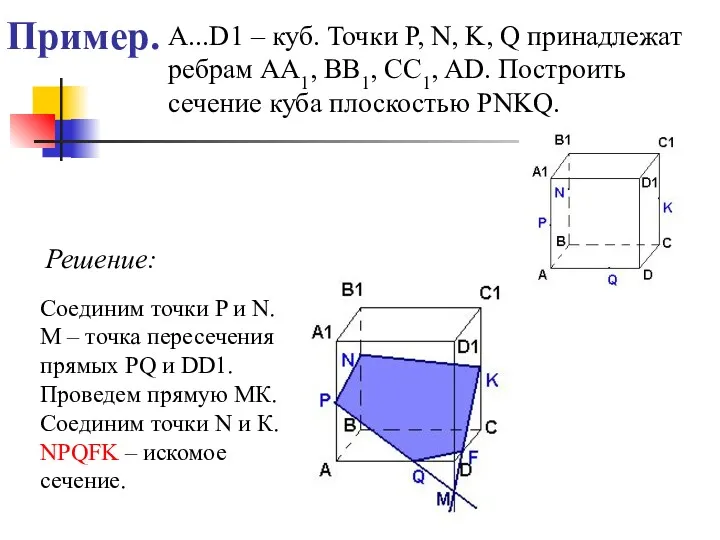
- 39. Пример. A...D1 – куб. Точки P, N, K, Q принадлежат ребрам AA1, BB1, CC1, AD. Построить
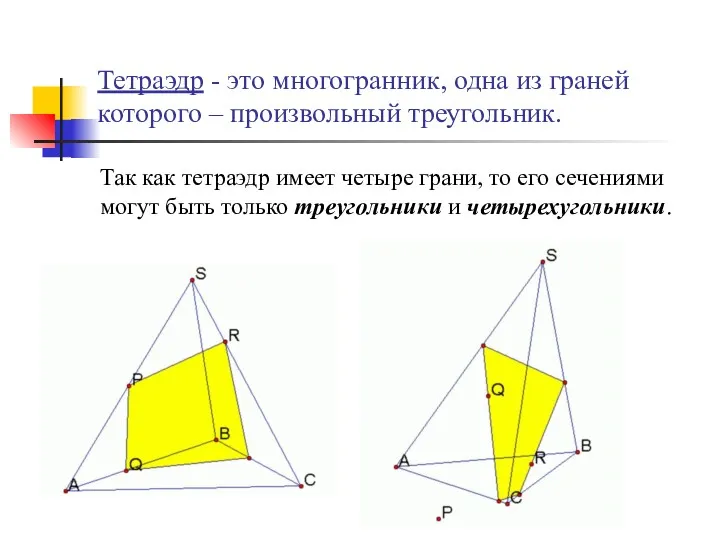
- 40. Тетраэдр - это многогранник, одна из граней которого – произвольный треугольник. Так как тетраэдр имеет четыре
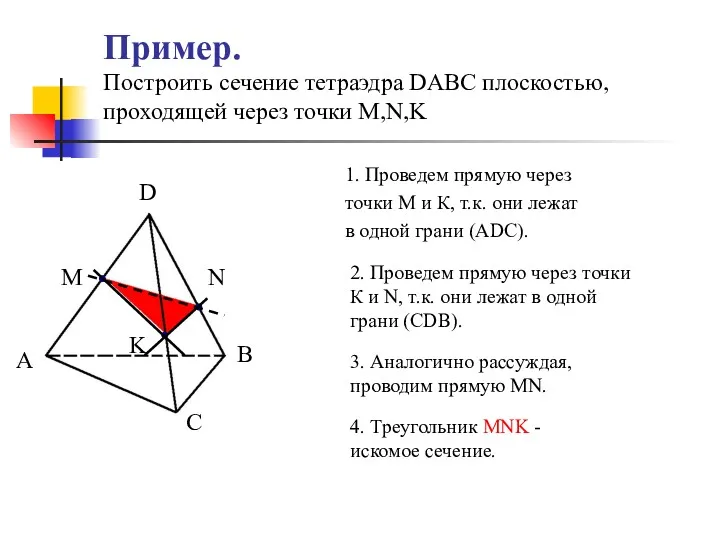
- 41. Пример. Построить сечение тетраэдра DABC плоскостью, проходящей через точки M,N,K 1. Проведем прямую через точки М
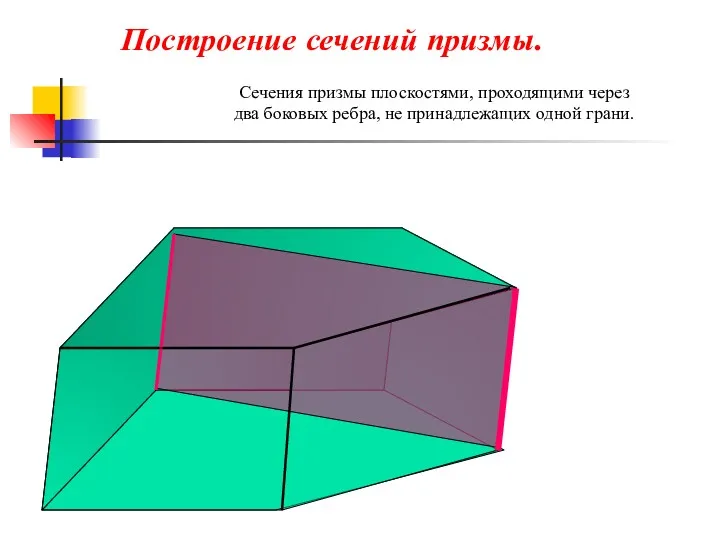
- 42. Сечения призмы плоскостями, проходящими через два боковых ребра, не принадлежащих одной грани. Построение сечений призмы.
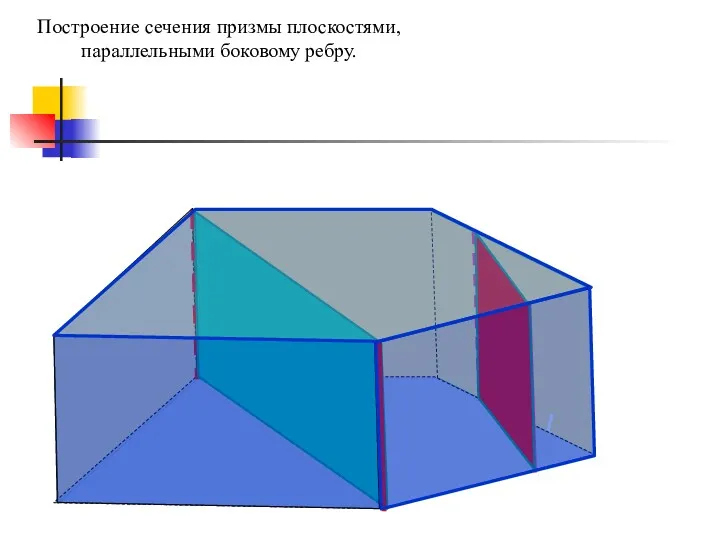
- 43. Построение сечения призмы плоскостями, параллельными боковому ребру.
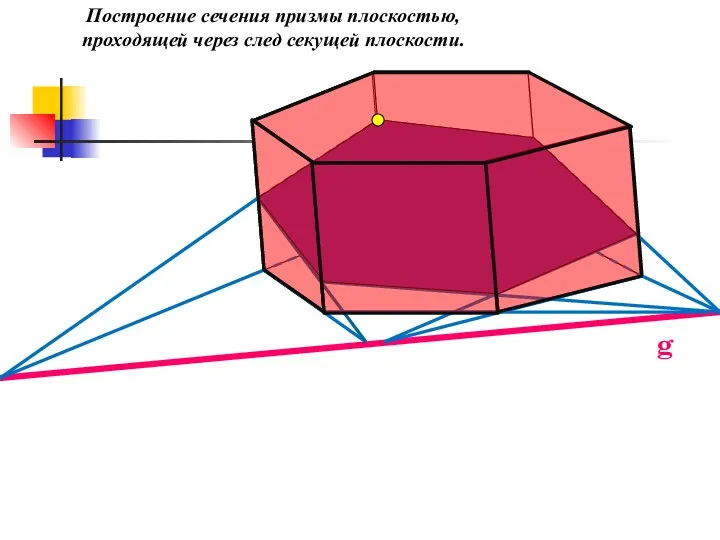
- 44. g Построение сечения призмы плоскостью, проходящей через след секущей плоскости.
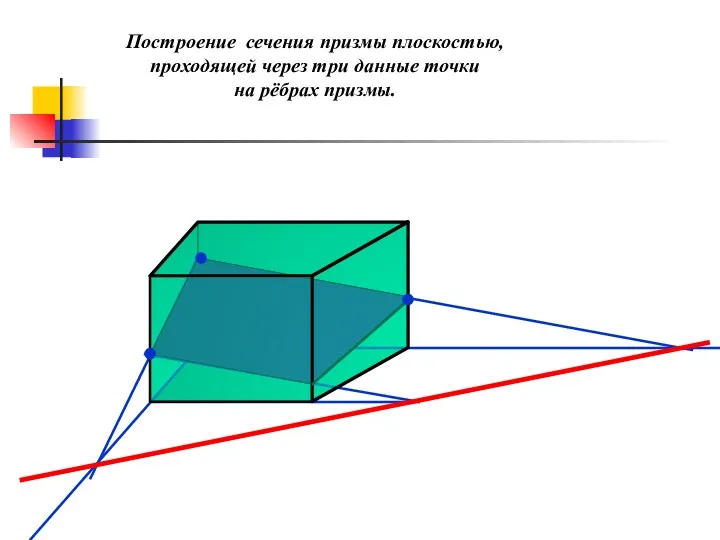
- 45. Построение сечения призмы плоскостью, проходящей через три данные точки на рёбрах призмы.
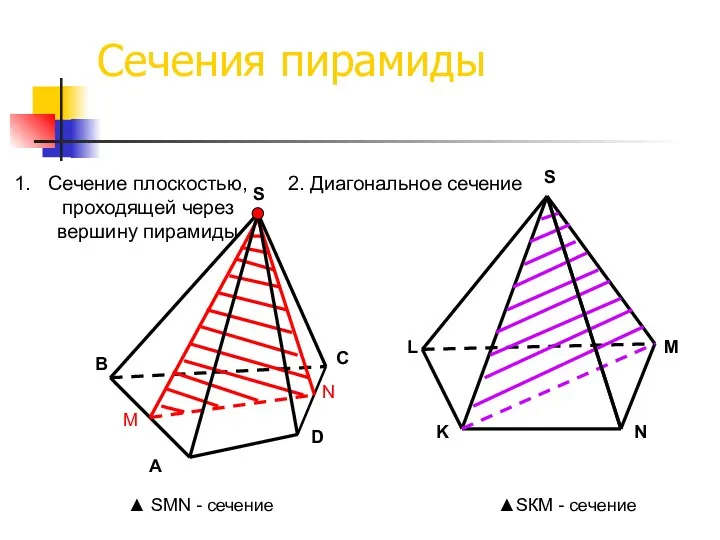
- 46. Сечения пирамиды А В С D S Сечение плоскостью, проходящей через вершину пирамиды 2. Диагональное сечение
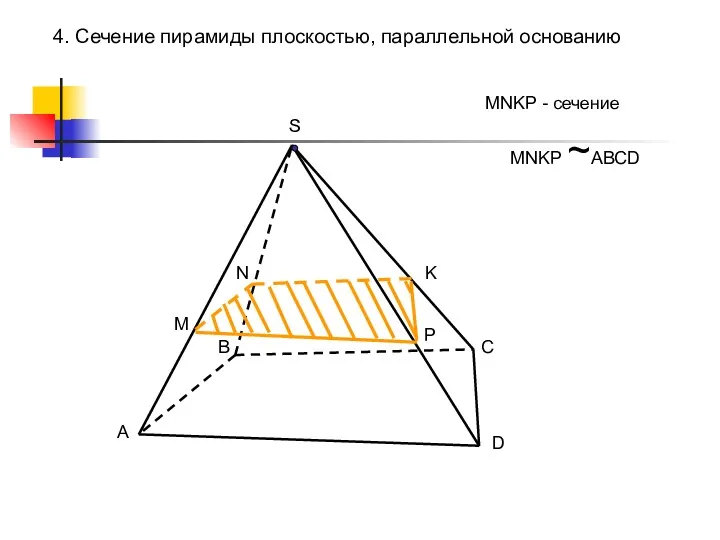
- 47. 4. Сечение пирамиды плоскостью, параллельной основанию A B C D S M N K P MNKP
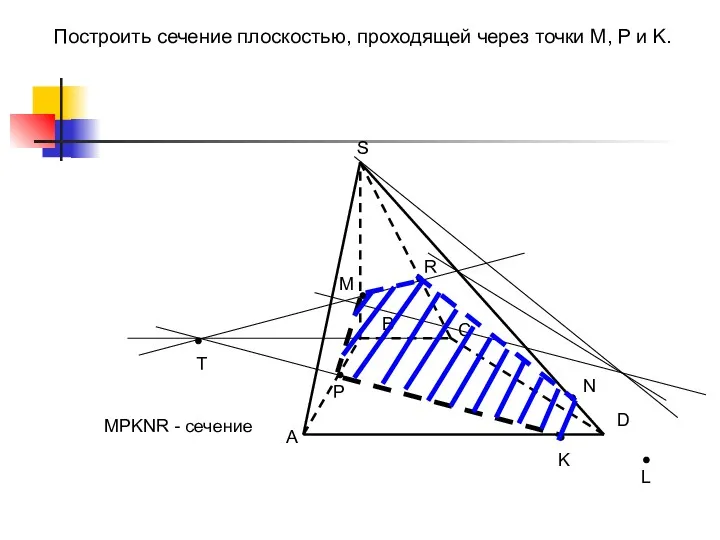
- 48. Построить сечение плоскостью, проходящей через точки M, P и K. A B C D S L
- 50. Скачать презентацию














 Решение систем уравнений способом подстановки
Решение систем уравнений способом подстановки Математическое кафе
Математическое кафе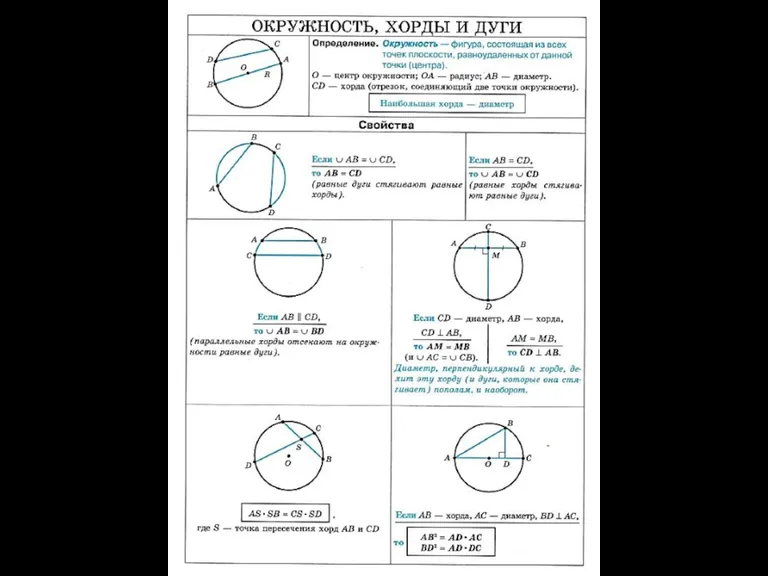 Окружность, хорді и дуги
Окружность, хорді и дуги Умножение в случаях вида 23 • 40
Умножение в случаях вида 23 • 40 Дифференциальные уравнения и системы
Дифференциальные уравнения и системы Из опыта работы по подготовке учащихся 9-х классов к ОГЭ по математике
Из опыта работы по подготовке учащихся 9-х классов к ОГЭ по математике Влияние поисково-исследовательской деятельности на развитие логико-конструктивного мышления и формирование математических способностей дошкольников (презентация)
Влияние поисково-исследовательской деятельности на развитие логико-конструктивного мышления и формирование математических способностей дошкольников (презентация) Метод проектов в учебной деятельности
Метод проектов в учебной деятельности Длина окружности. Площадь круга
Длина окружности. Площадь круга Трапеция. Решение задач
Трапеция. Решение задач Многогранники
Многогранники Электронное сопровождение заданий учебника математики 2 класса, часть 1 (автор Н. Б. Истомина)для фронтальной работы с интерактивной доской1-я четверть
Электронное сопровождение заданий учебника математики 2 класса, часть 1 (автор Н. Б. Истомина)для фронтальной работы с интерактивной доской1-я четверть Линейные дифференциальные уравнения n-го порядка (однородные с постоянными коэффициентами, уравнения Эйлера)
Линейные дифференциальные уравнения n-го порядка (однородные с постоянными коэффициентами, уравнения Эйлера) тест 4 класс математика
тест 4 класс математика Деление трехзначного числа на однозначное, когда в частном есть нуль
Деление трехзначного числа на однозначное, когда в частном есть нуль Параллелепипед
Параллелепипед Презентация Таблица умножения. 3 класс.
Презентация Таблица умножения. 3 класс. Неевклидова геометрия
Неевклидова геометрия Параллелограмм и его свойства
Параллелограмм и его свойства Своя игра по математике в 5 классе
Своя игра по математике в 5 классе Итоговый тест по математике, 4 класс, часть 1
Итоговый тест по математике, 4 класс, часть 1 Умножение на 10, 100, 1000
Умножение на 10, 100, 1000 Умножение рациональных чисел
Умножение рациональных чисел Сравнение величин углов. Классификация углов по градусной мере
Сравнение величин углов. Классификация углов по градусной мере Многоугольники, описанные около окружности. Геометрия, 8 класс
Многоугольники, описанные около окружности. Геометрия, 8 класс Нахождение неизвестного третьего слагаемого. Задачи
Нахождение неизвестного третьего слагаемого. Задачи Систематические погрешности
Систематические погрешности Повторение Курса математики 6 - 7 класса
Повторение Курса математики 6 - 7 класса