Содержание
- 2. ИСТОРИЧЕСКАЯ СПРАВКА Математический анализ как раздел математики возник в результате объединения двух различных и первоначально не
- 3. ИСТОРИЧЕСКАЯ СПРАВКА Ферма также занимался задачами, которые мы сейчас относим к дифференциальному исчислению – проведением касательных
- 4. ГО́ТФРИД ВИ́ЛЬГЕЛЬМ ЛЕ́ЙБНИЦ (GOTTFRIED WILHELM VON LEIBNIZ) Лейбниц, независимо от Ньютона, создал математический анализ — дифференциальное
- 5. ЛЕКЦИЯ 1. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ Понятие производной. Геометрический и физический смысл производной. Основные теоремы дифференциального исчисления. Дифференцирование
- 6. ПОНЯТИЕ ПРОИЗВОДНОЙ Понятие производной является одним из основных математических понятий. Производная широко используется при решении ряда
- 7. ПОНЯТИЕ ПРОИЗВОДНОЙ
- 8. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ
- 9. ФИЗИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
- 10. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
- 11. ОСНОВНЫЕ ТЕОРЕМЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
- 12. ОСНОВНЫЕ ТЕОРЕМЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
- 13. ОСНОВНЫЕ ТЕОРЕМЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
- 14. ПРОИЗВОДНЫЕ ОСНОВНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ (u=u(x))
- 15. ПРИМЕРЫ
- 16. ЛОГАРИФМИЧЕСКОЕ ДИФФЕРЕНЦИРОВАНИЕ
- 17. ЛОГАРИФМИЧЕСКОЕ ДИФФЕРЕНЦИРОВАНИЕ
- 18. ЛОГАРИФМИЧЕСКОЕ ДИФФЕРЕНЦИРОВАНИЕ
- 19. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ, ЗАДАННЫХ ПАРАМЕТРИЧЕСКИ
- 20. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ Функции одной независимой переменной не охватывают все зависимости, существующие в природе. Поэтому
- 21. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- 22. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- 23. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ Таким образом, частная производная функции нескольких (двух, трех и больше ) переменных
- 24. ПРИМЕРЫ
- 25. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ Конечно-разностная аппроксимация производной - формула левых разностей - формула правых разностей - формула
- 26. ПРИМЕРЫ Рассчитать приближенные значения производной функции f(x)=x2 на отрезке [1,2] с шагом 0,1, сравнить с точными
- 28. Скачать презентацию
























![ПРИМЕРЫ Рассчитать приближенные значения производной функции f(x)=x2 на отрезке [1,2]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/68989/slide-25.jpg)
 Творческий проект Станок-лобзик универсальный стационарный
Творческий проект Станок-лобзик универсальный стационарный Образование причастий: обобщение
Образование причастий: обобщение Монтаж высотных сооружений
Монтаж высотных сооружений Модель коррекции результатов обучения авиадиспетчеров радиообмену на английском языке
Модель коррекции результатов обучения авиадиспетчеров радиообмену на английском языке Презентация Пословицы и поговорки о чае и чаепитии
Презентация Пословицы и поговорки о чае и чаепитии Чудесные цветники весной
Чудесные цветники весной ПОСЛЕДНИЙ ЗВОНОК
ПОСЛЕДНИЙ ЗВОНОК Упражнение для глаз. Состроили глазки
Упражнение для глаз. Состроили глазки Задания по теме Источники права
Задания по теме Источники права Развитие представлений о возникновении жизни на Земле
Развитие представлений о возникновении жизни на Земле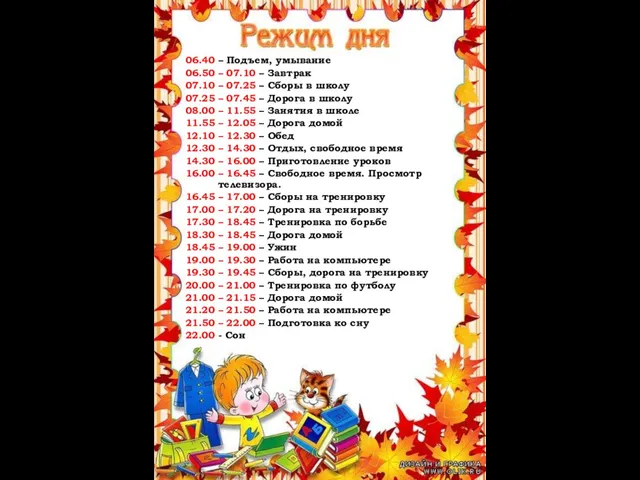 Распорядок дня школьника
Распорядок дня школьника Понятие, система, задачи, принципы уголовного права. Уголовная политика. Наука уголовного права
Понятие, система, задачи, принципы уголовного права. Уголовная политика. Наука уголовного права брейн-ринг в 6 классе Рельеф Земли
брейн-ринг в 6 классе Рельеф Земли Агрессивные дети
Агрессивные дети Неметаллические материалы и полиамиды
Неметаллические материалы и полиамиды Технология портфолио как инструмент выявления уровня форсированности компетенций выпускника
Технология портфолио как инструмент выявления уровня форсированности компетенций выпускника История возникновения этикета
История возникновения этикета Проект Работаем с папой
Проект Работаем с папой Гендерная сегментация потребителей. Женщины как потребители
Гендерная сегментация потребителей. Женщины как потребители 26 июня - Международный день борьбы с наркотиками
26 июня - Международный день борьбы с наркотиками Весна
Весна Формы контроля знаний
Формы контроля знаний Системы линейных уравнений с двумя переменными. Терминологический словарь
Системы линейных уравнений с двумя переменными. Терминологический словарь Питание. Пищевые добавки.
Питание. Пищевые добавки. Рекомендации по библиографическому описанию документа, в списке использованных источников и литературы
Рекомендации по библиографическому описанию документа, в списке использованных источников и литературы Логарифмы. Определение логарифма
Логарифмы. Определение логарифма Связь производных индолизина и трополона с медициной
Связь производных индолизина и трополона с медициной Трудоустройство выпускников Казанского федерального университета
Трудоустройство выпускников Казанского федерального университета