Виды проецирования. Признак принадлежности точки – прямой. Деление отрезка прямой в заданном отношении. Теорема Фалеса презентация
Содержание
- 2. Целью дисциплины является формирование у студента системы теоретических знаний об основных способах построения изображения пространственных форм
- 3. Трудоемкость дисциплины составляет 5 зачетных единиц, 180 час ( в том числе: 64 часа лекционных ,
- 4. Темы, рассматриваемые в 1 семестре Ортогональные проекции точки, прямой, плоскости. Методы преобразования проекций. Кривые линии и
- 5. Лекция 1 Виды проецирования. Образование комплексного чертежа. Точка. Проекции точки. Конкурирующие точки. Прямая. Образование прямой линии.
- 6. Символы и обозначения графических элементов _
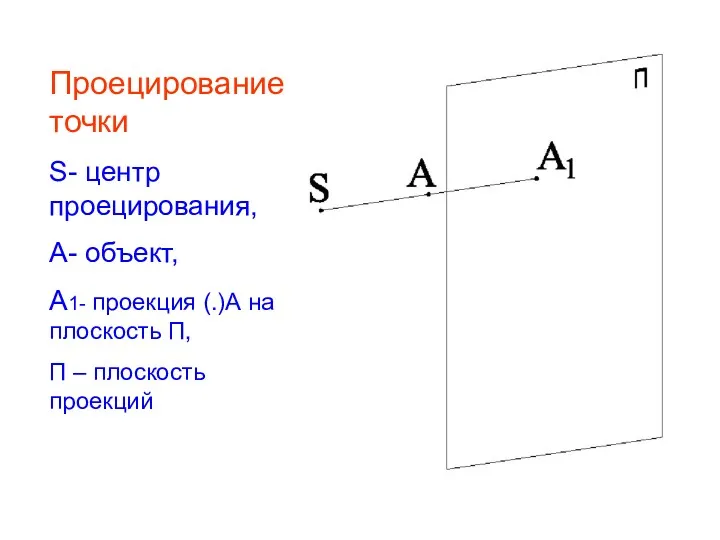
- 7. Проецирование точки S- центр проецирования, А- объект, А1- проекция (.)А на плоскость П, П – плоскость
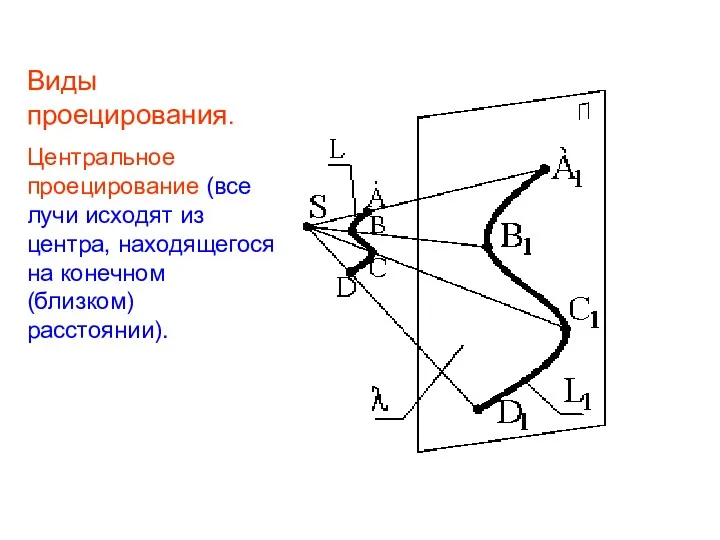
- 8. Виды проецирования. Центральное проецирование (все лучи исходят из центра, находящегося на конечном (близком) расстоянии).
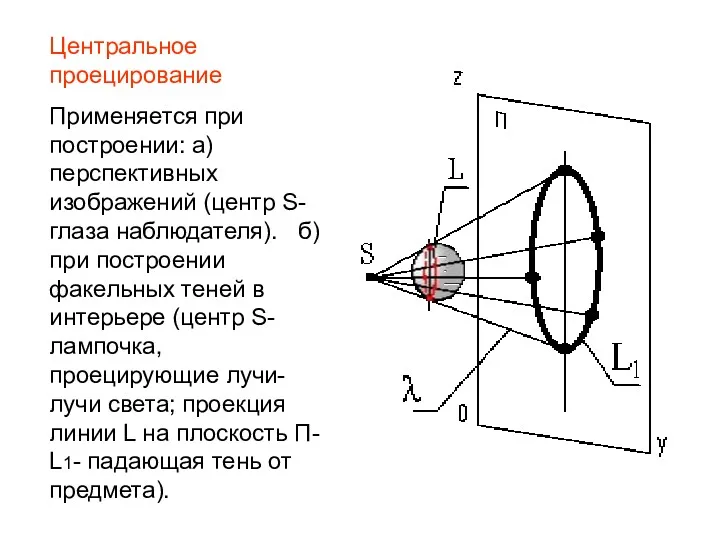
- 9. Центральное проецирование Применяется при построении: а)перспективных изображений (центр S- глаза наблюдателя). б) при построении факельных теней
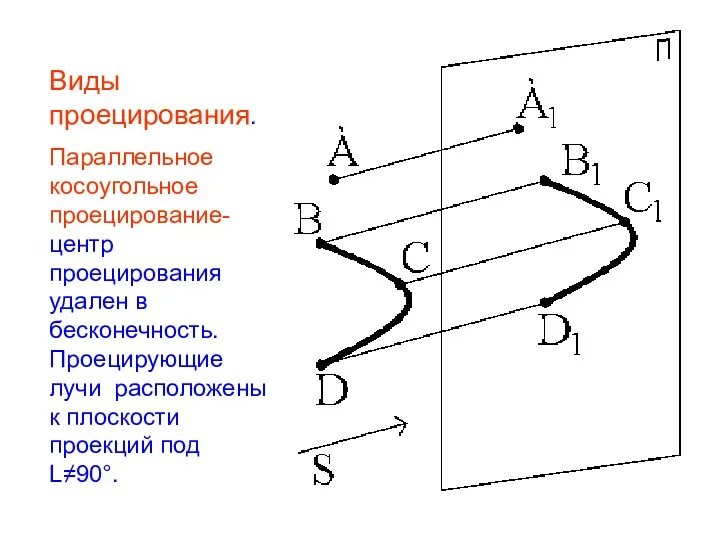
- 10. Виды проецирования. Параллельное косоугольное проецирование- центр проецирования удален в бесконечность. Проецирующие лучи расположены к плоскости проекций
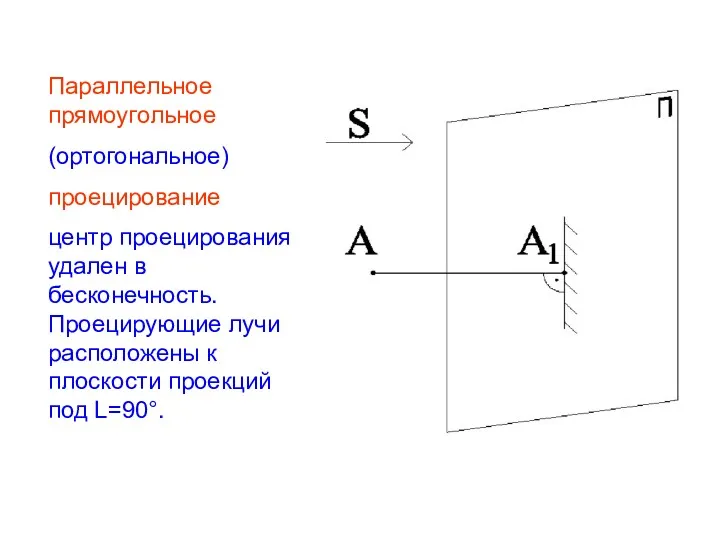
- 11. Параллельное прямоугольное (ортогональное) проецирование центр проецирования удален в бесконечность. Проецирующие лучи расположены к плоскости проекций под
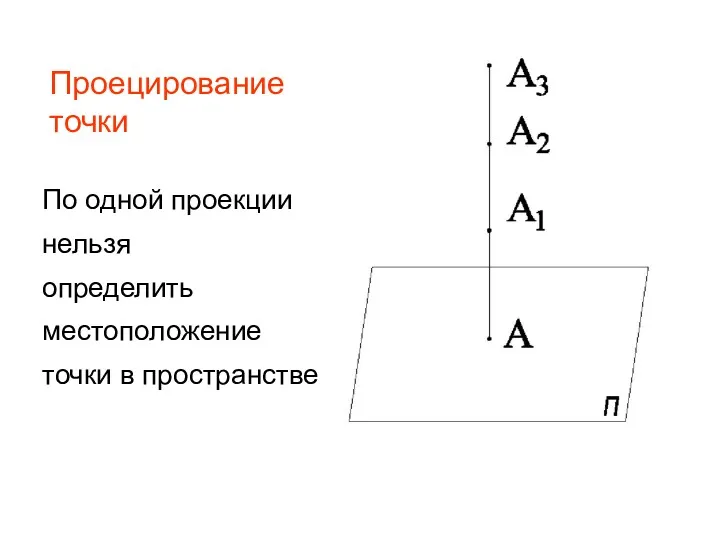
- 12. Проецирование точки По одной проекции нельзя определить местоположение точки в пространстве
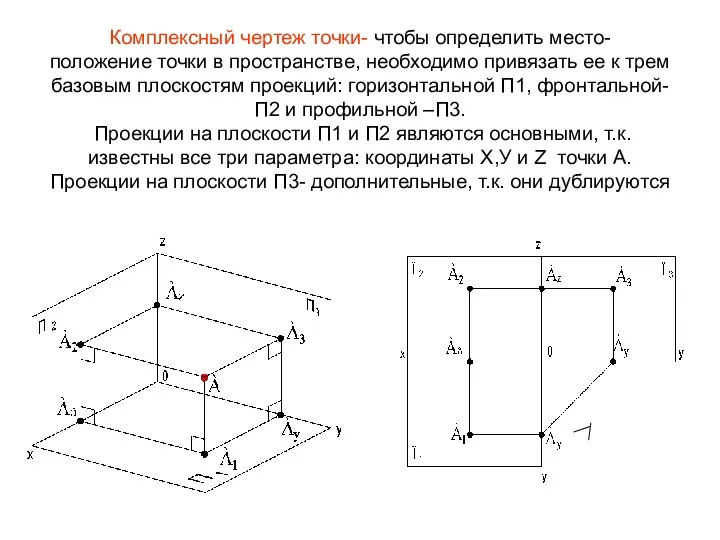
- 13. Комплексный чертеж точки- чтобы определить место- положение точки в пространстве, необходимо привязать ее к трем базовым
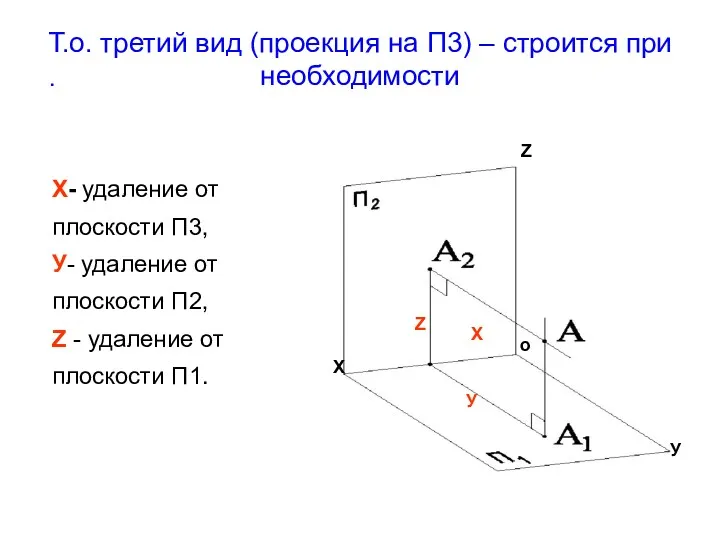
- 14. . Т.о. третий вид (проекция на П3) – строится при необходимости Х- удаление от плоскости П3,
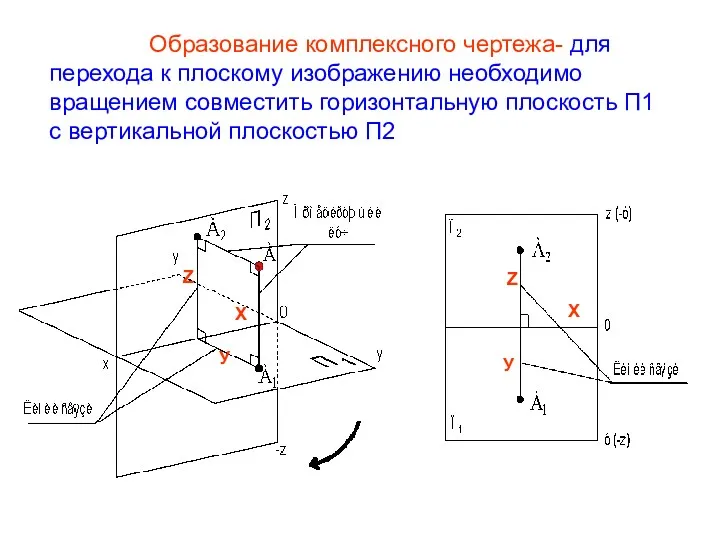
- 15. Образование комплексного чертежа- для перехода к плоскому изображению необходимо вращением совместить горизонтальную плоскость П1 с вертикальной
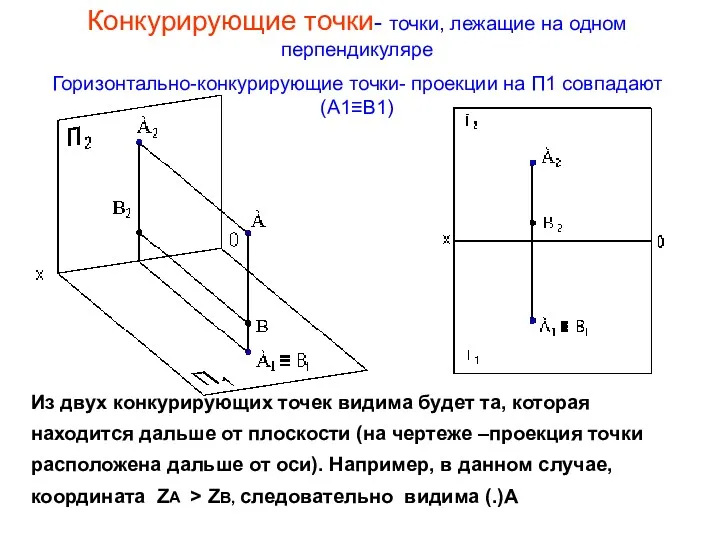
- 16. Конкурирующие точки- точки, лежащие на одном перпендикуляре Горизонтально-конкурирующие точки- проекции на П1 совпадают (А1≡В1) Из двух
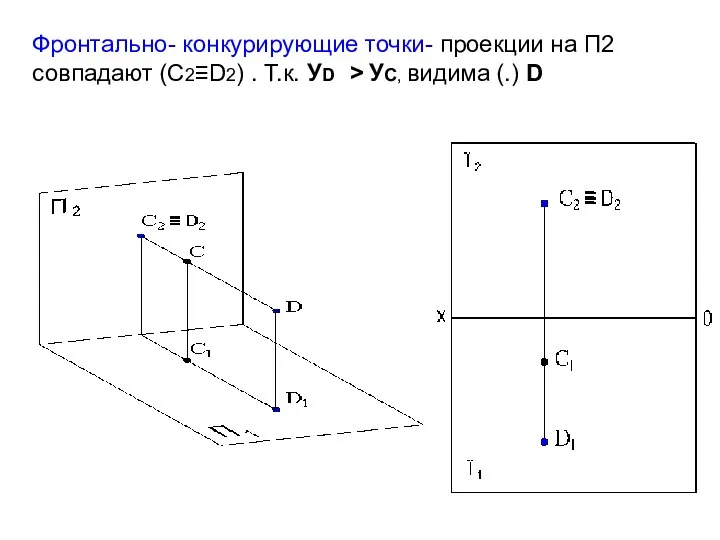
- 17. Фронтально- конкурирующие точки- проекции на П2 совпадают (С2≡D2) . Т.к. УD > УС, видима (.) D
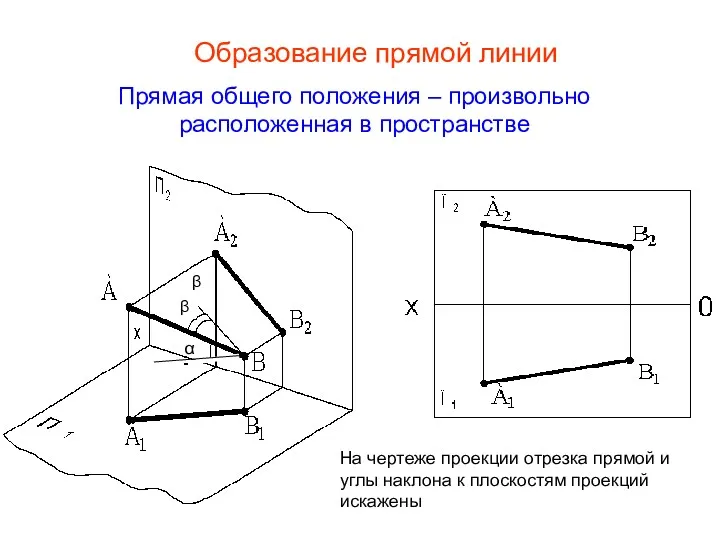
- 18. Образование прямой линии Прямая общего положения – произвольно расположенная в пространстве β α β На чертеже
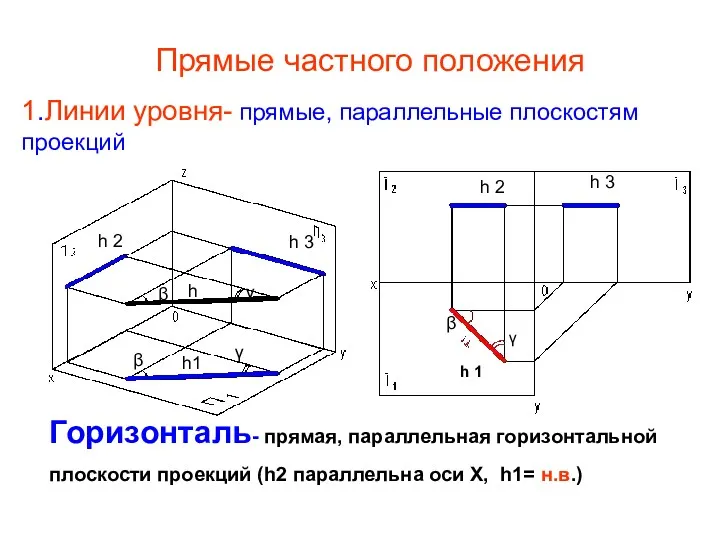
- 19. Прямые частного положения 1.Линии уровня- прямые, параллельные плоскостям проекций β γ h 1 γ h Горизонталь-
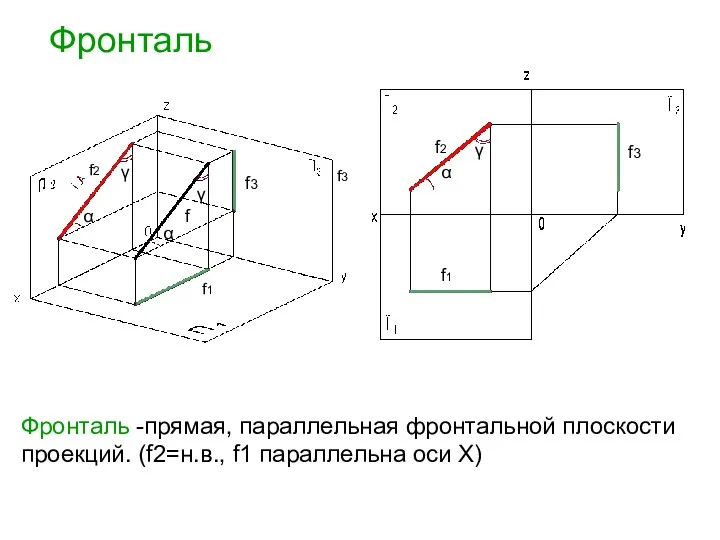
- 20. Фронталь f1 f3 f2 α f3 f1 f2 α γ α γ f Фронталь -прямая, параллельная
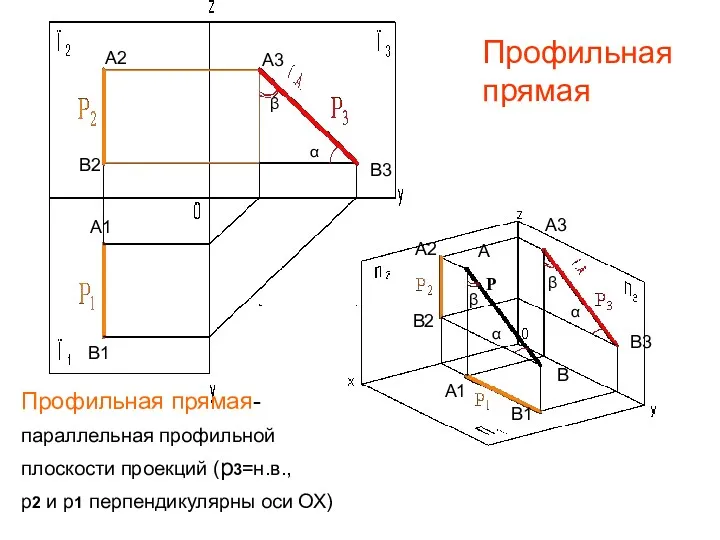
- 21. Профильная прямая β α α α β β P Профильная прямая- параллельная профильной плоскости проекций (р3=н.в.,
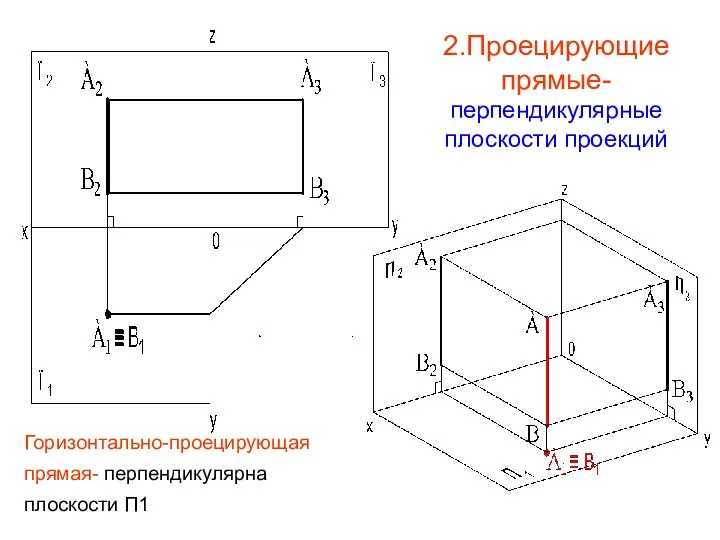
- 22. 2.Проецирующие прямые- перпендикулярные плоскости проекций Горизонтально-проецирующая прямая- перпендикулярна плоскости П1
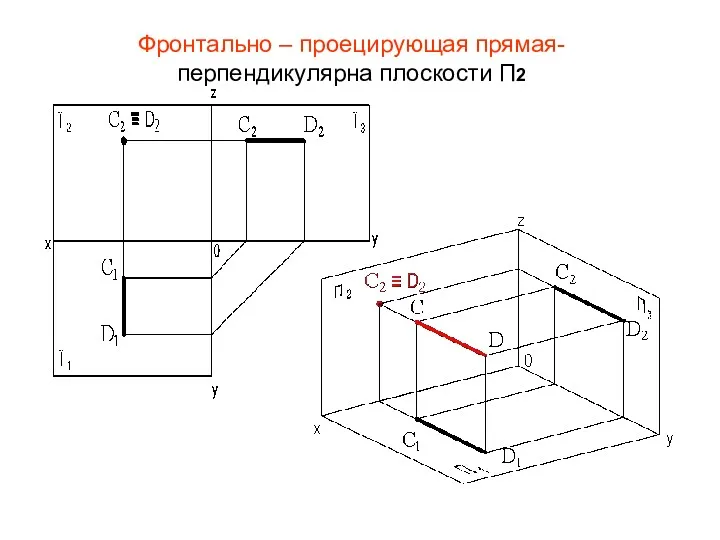
- 23. Фронтально – проецирующая прямая- перпендикулярна плоскости П2
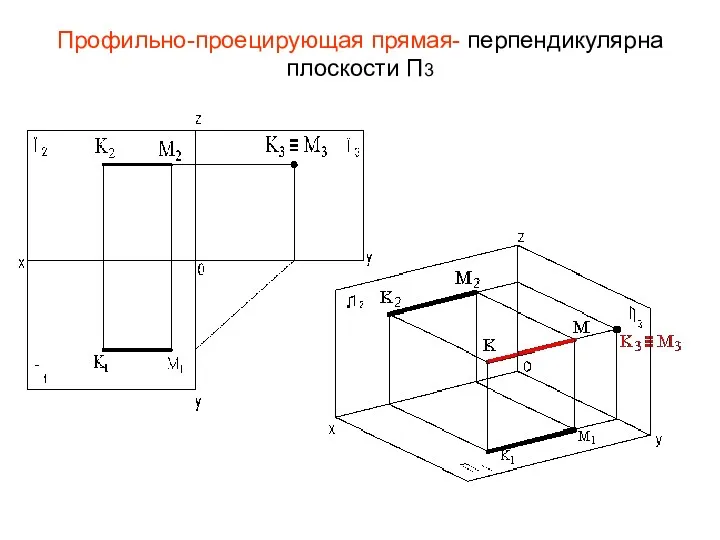
- 24. Профильно-проецирующая прямая- перпендикулярна плоскости П3
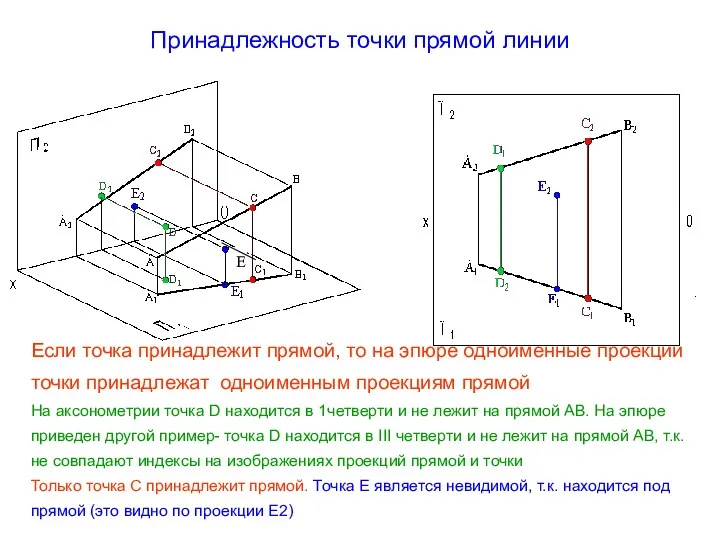
- 25. Принадлежность точки прямой линии Е Если точка принадлежит прямой, то на эпюре одноименные проекции точки принадлежат
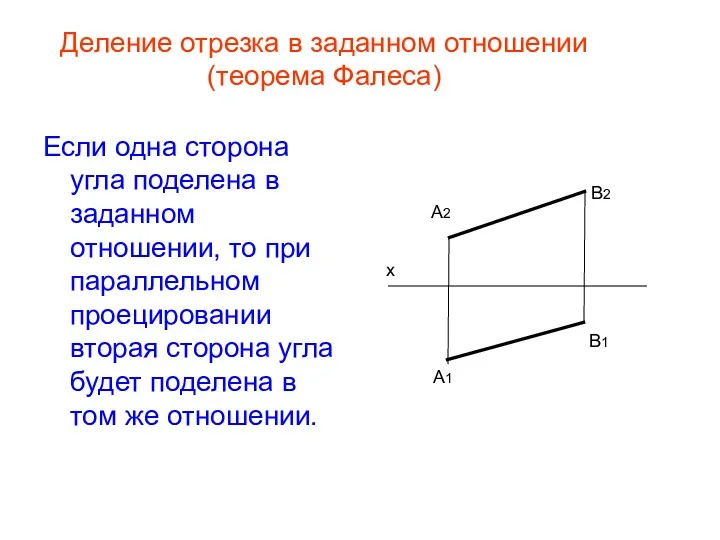
- 26. Деление отрезка в заданном отношении (теорема Фалеса) Если одна сторона угла поделена в заданном отношении, то
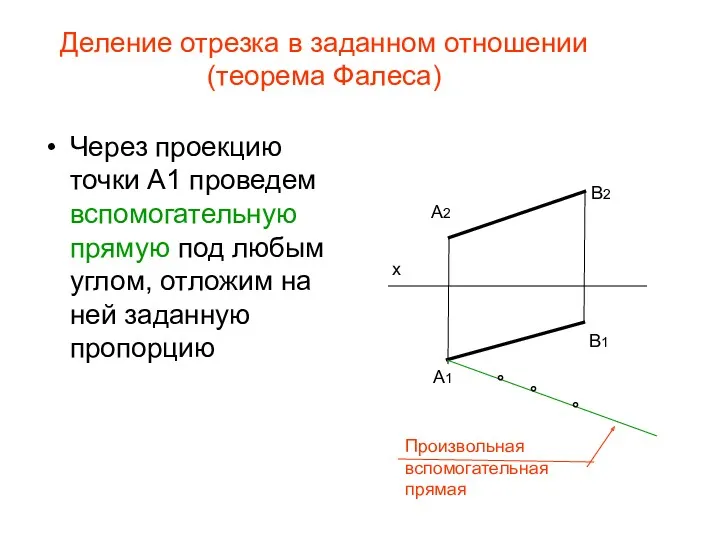
- 27. Деление отрезка в заданном отношении (теорема Фалеса) Через проекцию точки А1 проведем вспомогательную прямую под любым
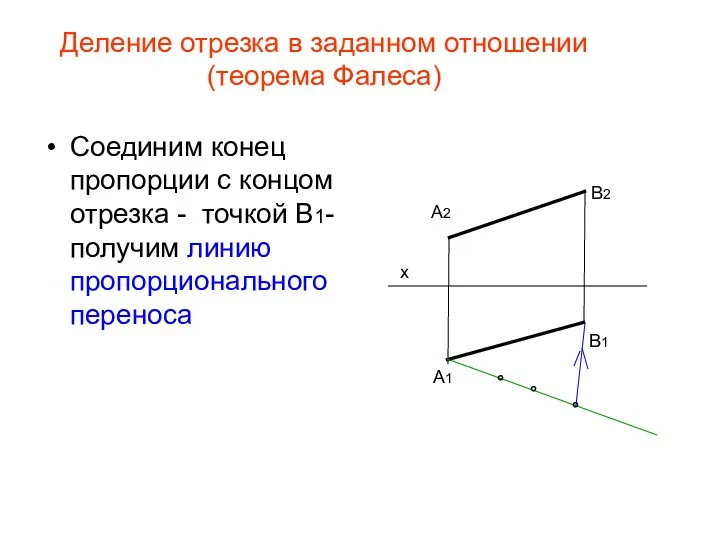
- 28. Деление отрезка в заданном отношении (теорема Фалеса) Соединим конец пропорции с концом отрезка - точкой В1-получим
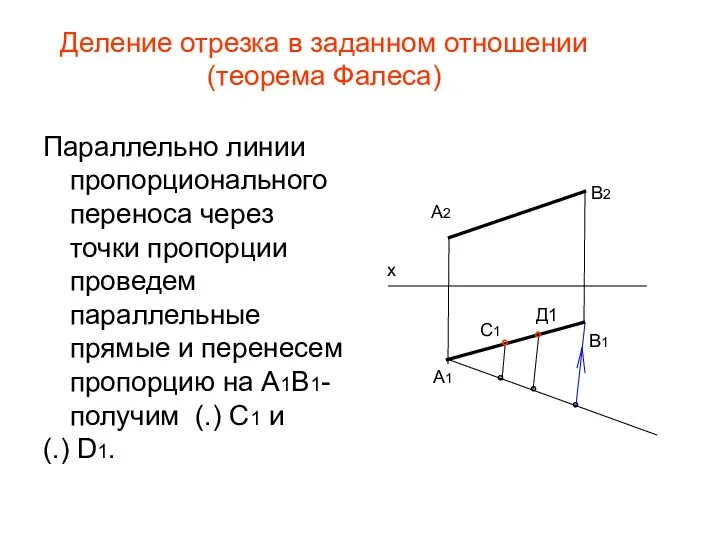
- 29. Деление отрезка в заданном отношении (теорема Фалеса) Параллельно линии пропорционального переноса через точки пропорции проведем параллельные
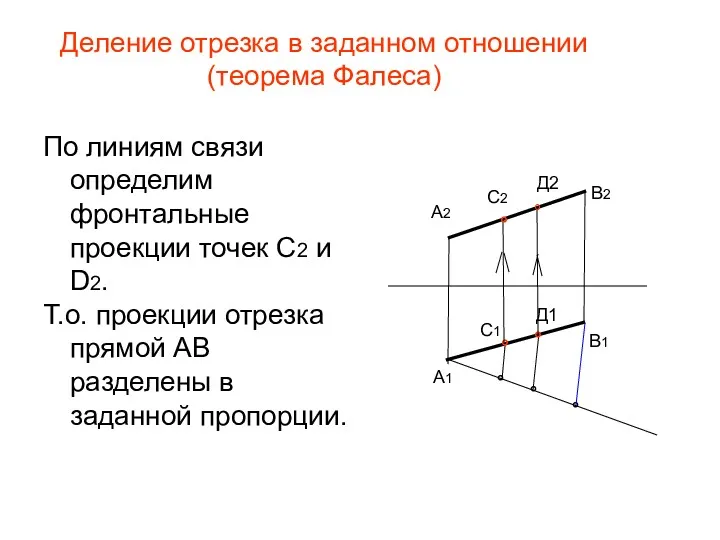
- 30. Деление отрезка в заданном отношении (теорема Фалеса) По линиям связи определим фронтальные проекции точек С2 и
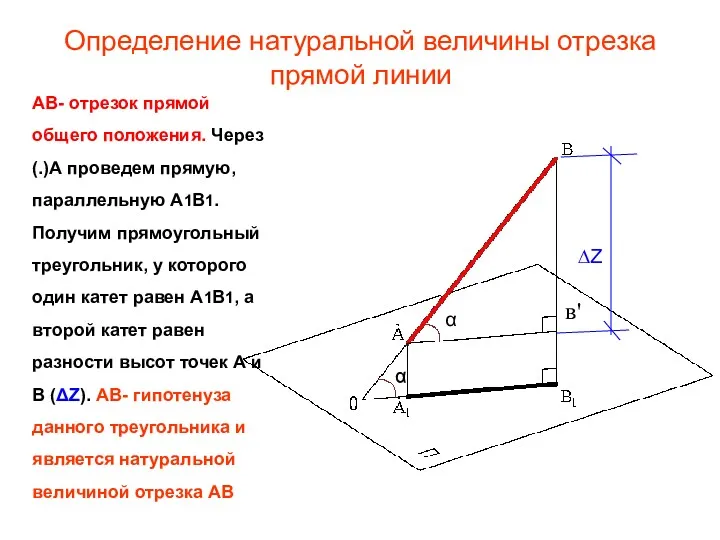
- 31. Определение натуральной величины отрезка прямой линии в' α α АВ- отрезок прямой общего положения. Через (.)А
- 32. Определение натуральной величины отрезка прямой линии Теорема: Натуральная величина отрезка прямой равна гипотенузе прямоугольного треугольника, у
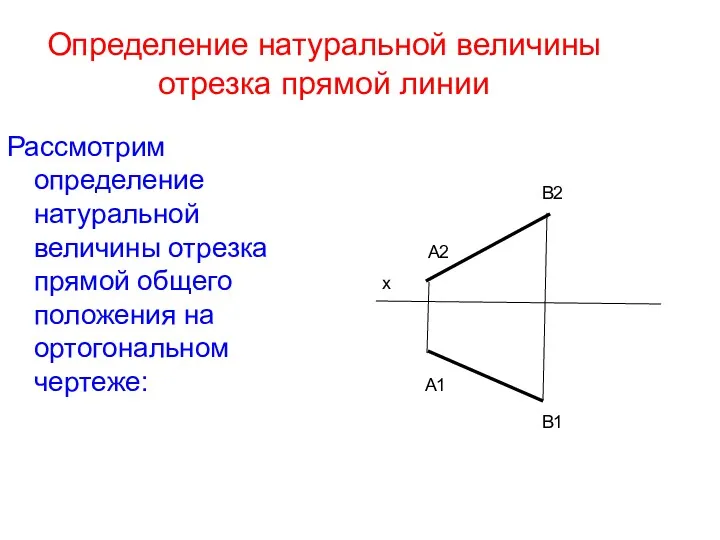
- 33. Определение натуральной величины отрезка прямой линии Рассмотрим определение натуральной величины отрезка прямой общего положения на ортогональном
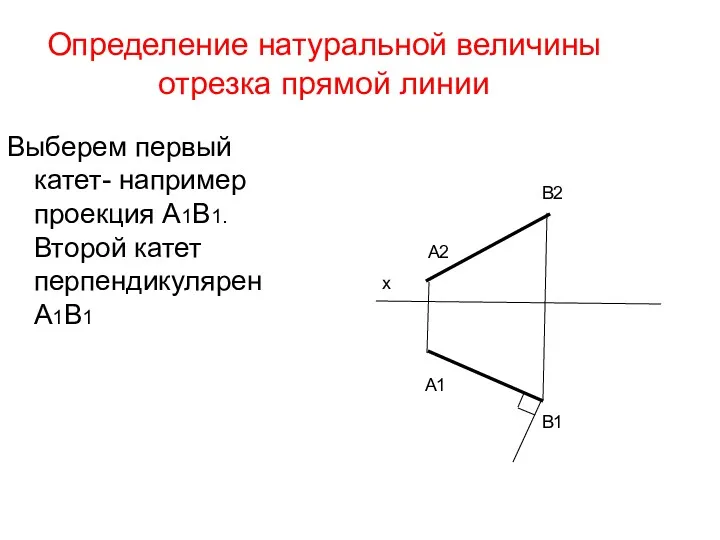
- 34. Определение натуральной величины отрезка прямой линии Выберем первый катет- например проекция А1В1. Второй катет перпендикулярен А1В1
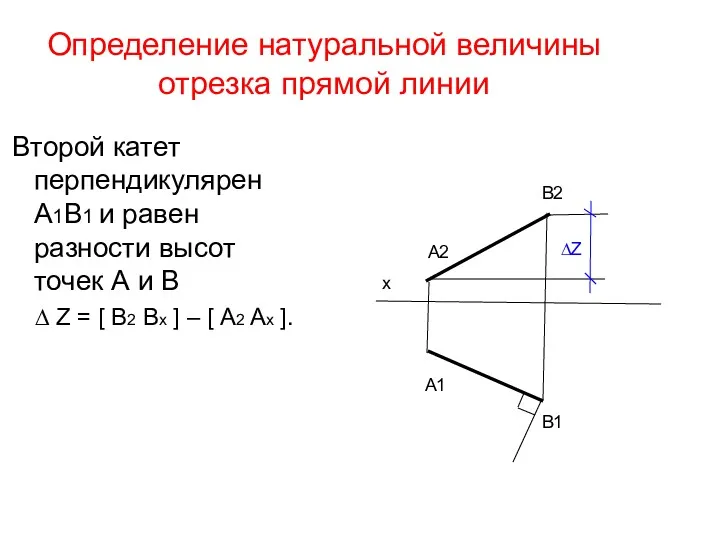
- 35. Определение натуральной величины отрезка прямой линии Второй катет перпендикулярен А1В1 и равен разности высот точек А
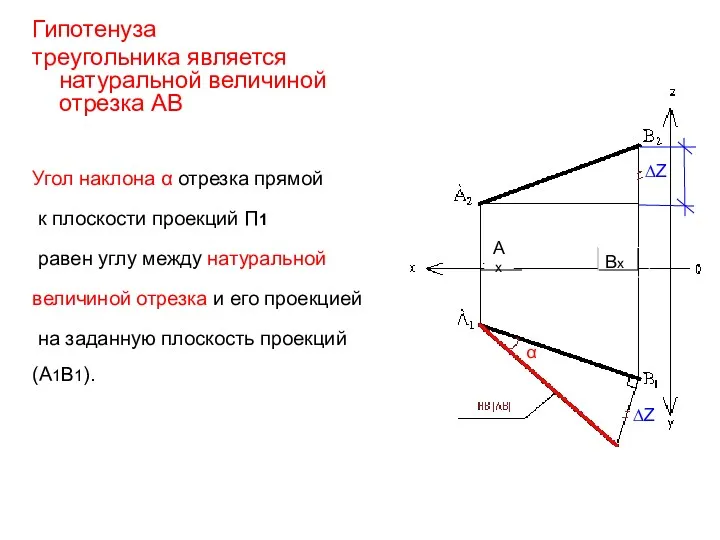
- 36. Гипотенуза треугольника является натуральной величиной отрезка АВ ∆Z ∆Z α Ах Вх Угол наклона α отрезка
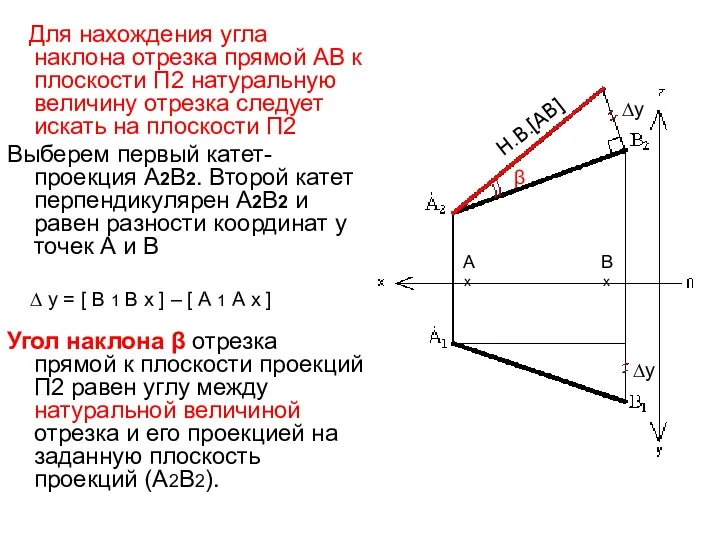
- 37. Для нахождения угла наклона отрезка прямой АВ к плоскости П2 натуральную величину отрезка следует искать на
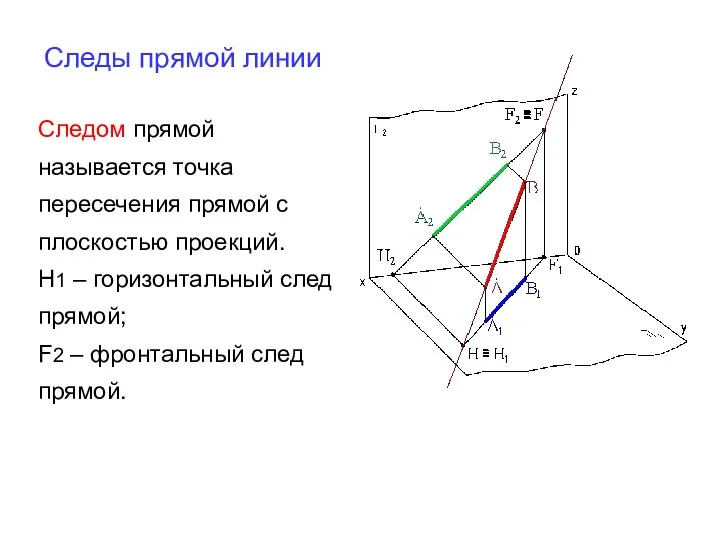
- 38. Следы прямой линии Следом прямой называется точка пересечения прямой с плоскостью проекций. Н1 – горизонтальный след
- 40. Скачать презентацию






 Нарезание резьбы
Нарезание резьбы Что такое резьба?
Что такое резьба? Технический рисунок
Технический рисунок Технический рисунок
Технический рисунок Чтение чертежей и технологической документации
Чтение чертежей и технологической документации Чертеж — конструкторский документ
Чертеж — конструкторский документ Плоскость. Следы плоскости. Частное положение плоскости. Главные линии плоскости. Взаимное положение двух плоскостей
Плоскость. Следы плоскости. Частное положение плоскости. Главные линии плоскости. Взаимное положение двух плоскостей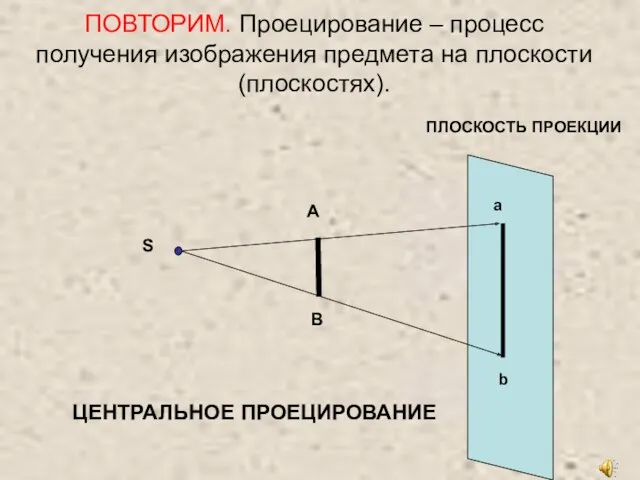 Проецирование – процесс получения изображения предмета на плоскости (плоскостях). 8 класс
Проецирование – процесс получения изображения предмета на плоскости (плоскостях). 8 класс Способы преобразования. Лекция 4
Способы преобразования. Лекция 4 Взаимное расположение двух прямых
Взаимное расположение двух прямых Проекции прямой( Лекция 2)
Проекции прямой( Лекция 2) Чтение и деталирование чертежа сборочной единицы
Чтение и деталирование чертежа сборочной единицы Резьба. Крепёжные изделия
Резьба. Крепёжные изделия Прямая и плоскость
Прямая и плоскость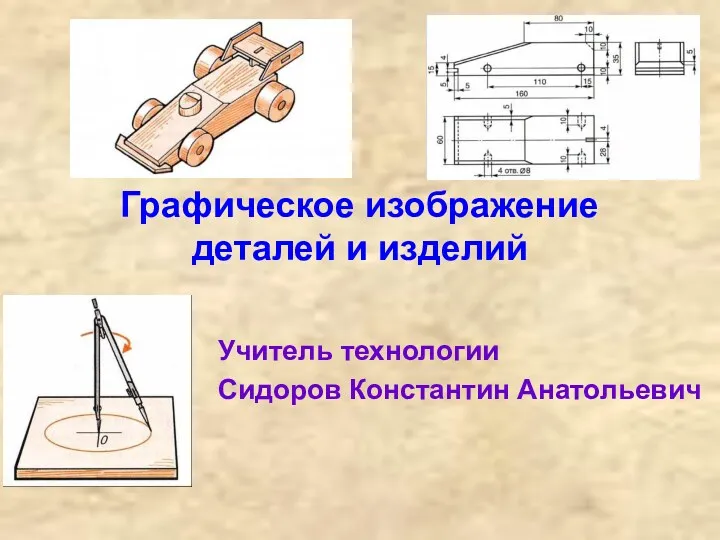 Графическое изображение деталей и изделий
Графическое изображение деталей и изделий Чертежные инструменты и методы работы с ними. Лекция 1
Чертежные инструменты и методы работы с ними. Лекция 1 Изображения - виды, разрезы, сечения
Изображения - виды, разрезы, сечения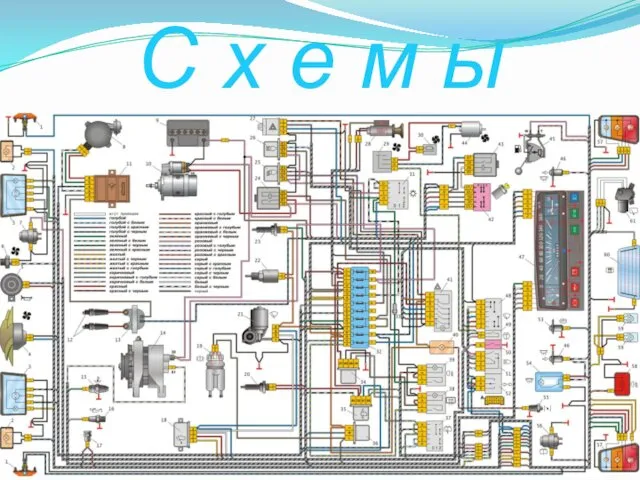 Схемы. Правила выполнения схем
Схемы. Правила выполнения схем Поверхности
Поверхности Прямоугольное проецирование
Прямоугольное проецирование Изображение и обозначение резьб
Изображение и обозначение резьб ANSYS в инженерных задачах
ANSYS в инженерных задачах Резьбовые соединения
Резьбовые соединения Построение теней от геометрических тел. Построение теней на архитектурных деталях. Лекция 13
Построение теней от геометрических тел. Построение теней на архитектурных деталях. Лекция 13 Общие правила выполнения чертежей деталей
Общие правила выполнения чертежей деталей Построение перспективы архитектурных деталей по одной точке схода (2 способ архитекторов)
Построение перспективы архитектурных деталей по одной точке схода (2 способ архитекторов) Изображение ландшафта средствами графики
Изображение ландшафта средствами графики 20231101_aksonometricheskie_proektsii_2
20231101_aksonometricheskie_proektsii_2