Содержание
- 2. 1. Движение свободной частицы Свободная частица – частица, движущаяся в отсутствие внешних полей. Т.к. на свободную
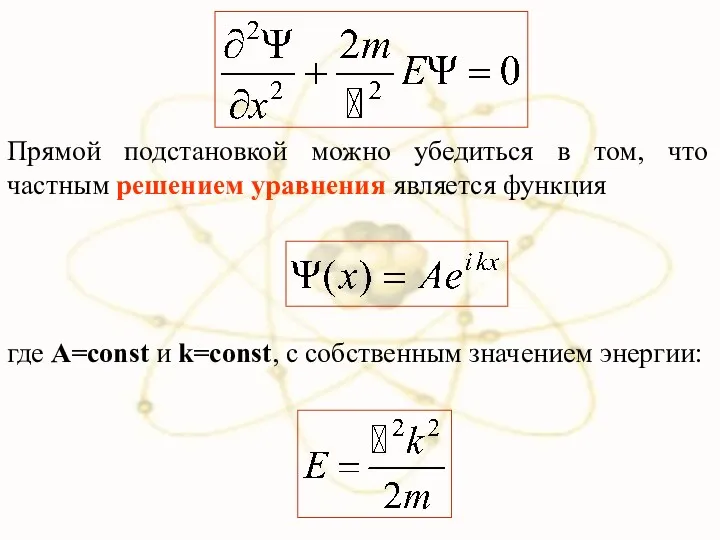
- 3. Прямой подстановкой можно убедиться в том, что частным решением уравнения является функция где A=const и k=const,
- 4. Зависимость энергии от импульса оказывается обычной для нерелятивистских частиц. Следовательно, энергия свободной частицы может принимать любые
- 5. Таким образом, свободная частица описывается плоской монохроматической волной де Бройля. Этому способствует не зависящая от времени
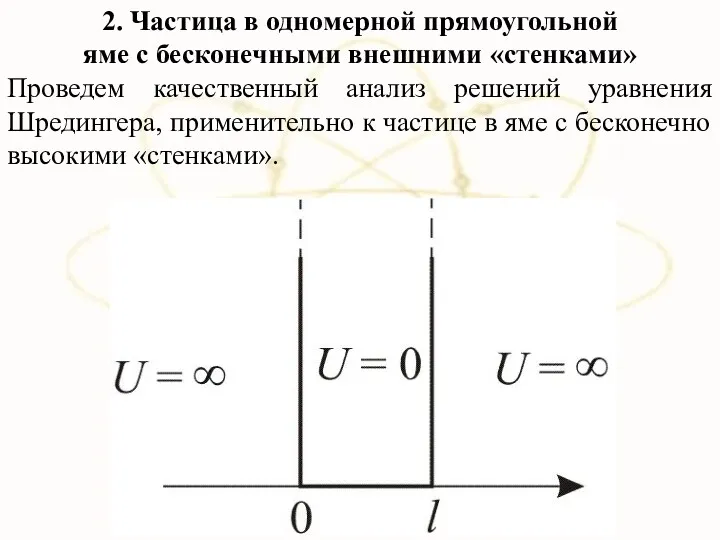
- 6. 2. Частица в одномерной прямоугольной яме с бесконечными внешними «стенками» Проведем качественный анализ решений уравнения Шредингера,
- 7. Такая яма описывается потенциальной энергией вида где l – ширина «ямы», энергия отсчитывается от ее дна.
- 8. Уравнение Шредингера для стационарных состояний в случае одномерной задачи запишется в виде:
- 9. По условию задачи (бесконечно высокие «стенки»), частица не проникает за пределы «ямы», поэтому вероятность ее обнаружения,
- 10. В пределах «ямы» (0 ≤ x ≤ l) уравнение Шредингера сведется к уравнению где Общее решение
- 11. Отсюда следует, что: где n = 1, 2, 3… Т.е. стационарное уравнение Шредингера описывающее движение частицы
- 12. Квантовые значения энергии En называется уровнями энергии, а число n, определяющее энергетические уровни - главным квантовым
- 13. Найдем собственные функции: Постоянную интегрирования А найдем из условия нормировки: В результате интегрирования получим Соответственные функции
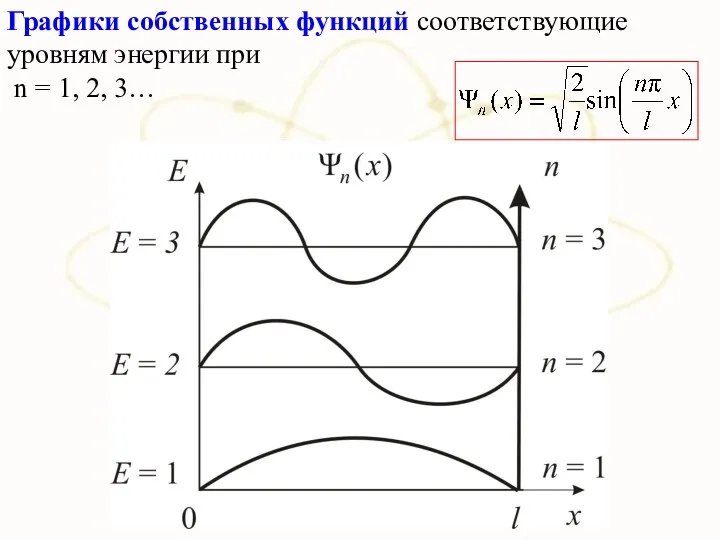
- 14. Графики собственных функций соответствующие уровням энергии при n = 1, 2, 3…
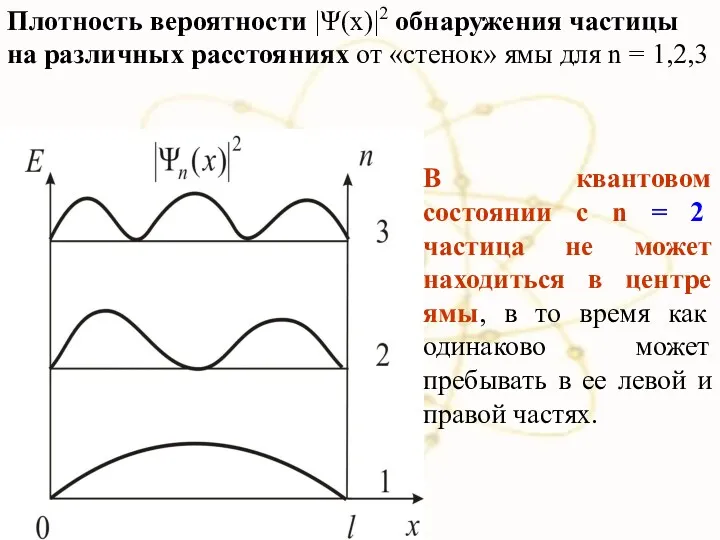
- 15. Плотность вероятности |Ψ(x)|2 обнаружения частицы на различных расстояниях от «стенок» ямы для n = 1,2,3 В
- 16. Из выражения следует, что энергетический интервал между двумя соседними условиями равен Например, для электрона при размерах
- 17. Если же размеры ямы соизмеримы с размерами стенки (l ≈ 10–10 м), то для электрона ΔEn
- 18. Кроме того, квантово-механическое рассмотрение этой задачи приводит к выводу, что частица в потенциальной яме с бесконечно
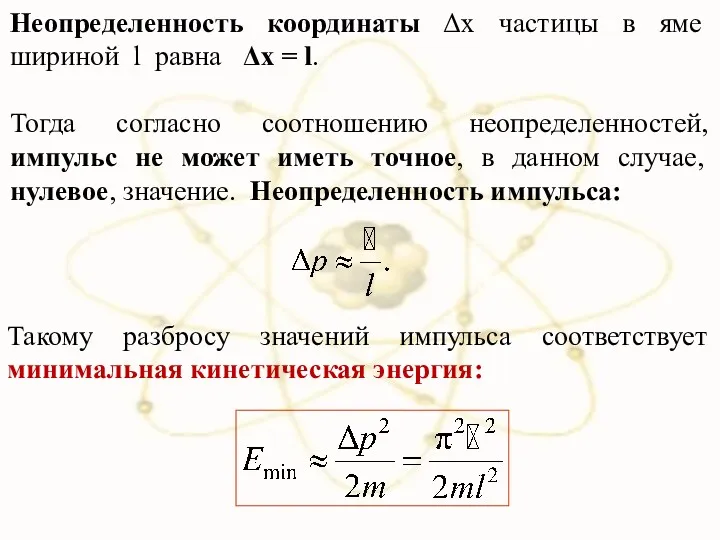
- 19. Неопределенность координаты Δx частицы в яме шириной l равна Δx = l. Тогда согласно соотношению неопределенностей,
- 20. При больших квантовых числах n>>1 т.е. соседние уровни расположены тесно: тем теснее, чем больше n. Если
- 21. Принцип соответствия: всякая новая, более общая теория, являющаяся развитием классической, не отвергает ее полностью, а включает
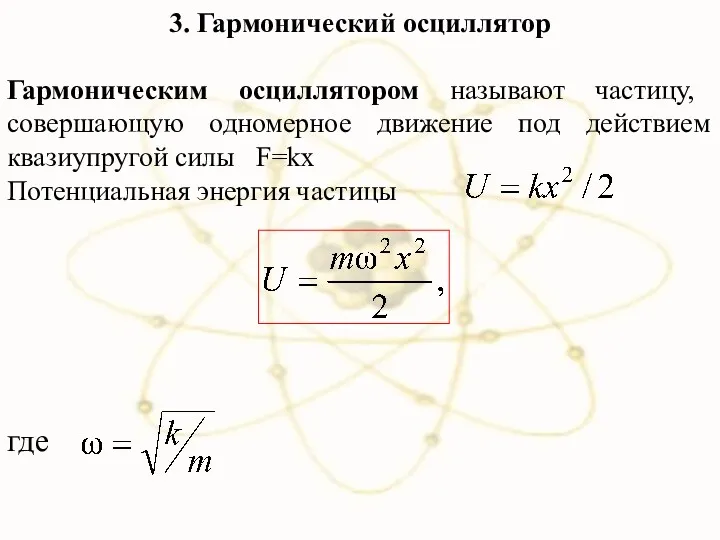
- 22. 3. Гармонический осциллятор Гармоническим осциллятором называют частицу, совершающую одномерное движение под действием квазиупругой силы F=kx Потенциальная
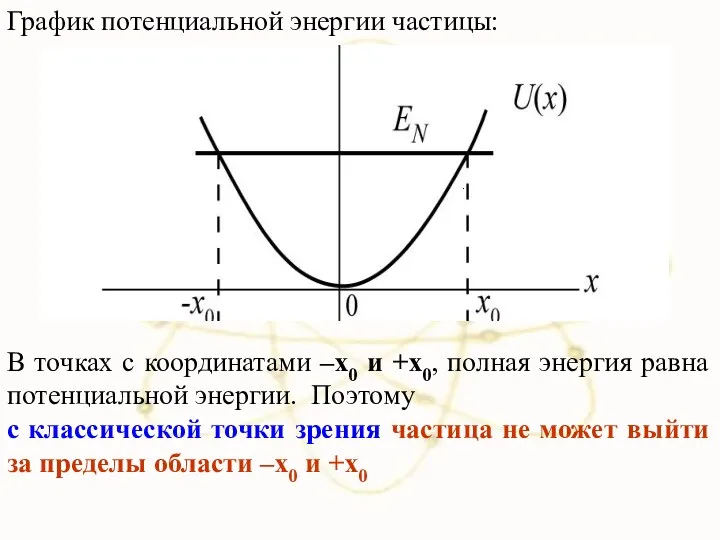
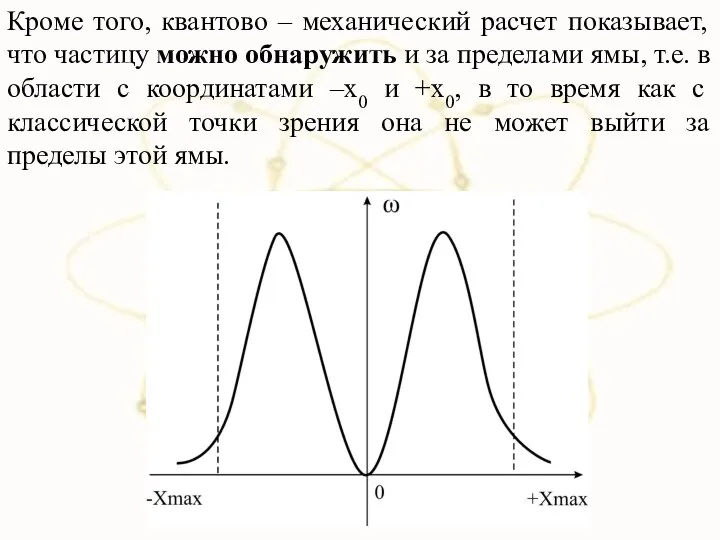
- 23. . В точках с координатами –x0 и +x0, полная энергия равна потенциальной энергии. Поэтому с классической
- 24. Гармонический осциллятор в квантовой механике - квантовый осциллятор - описывается уравнением Шредингера: Значения полной энергии осциллятора
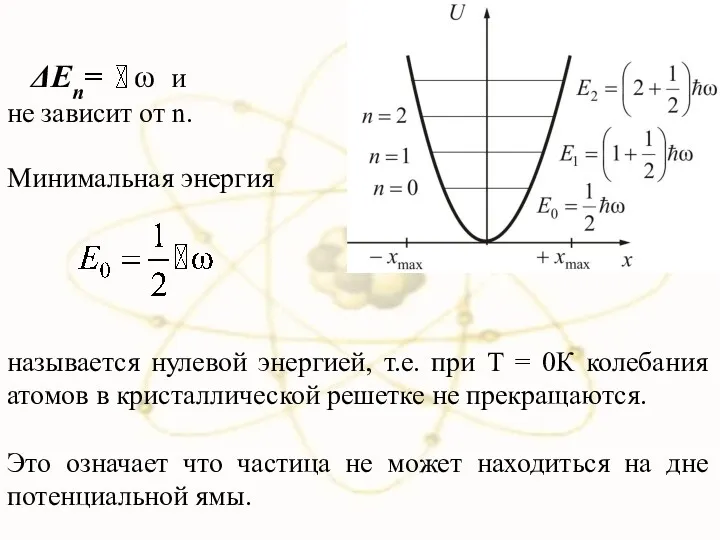
- 25. ΔEn= ω и не зависит от n. называется нулевой энергией, т.е. при Т = 0К колебания
- 26. В квантовой механике вычисляется вероятность различных переходов квантовой системы из одного состояния в другое. Для гармонического
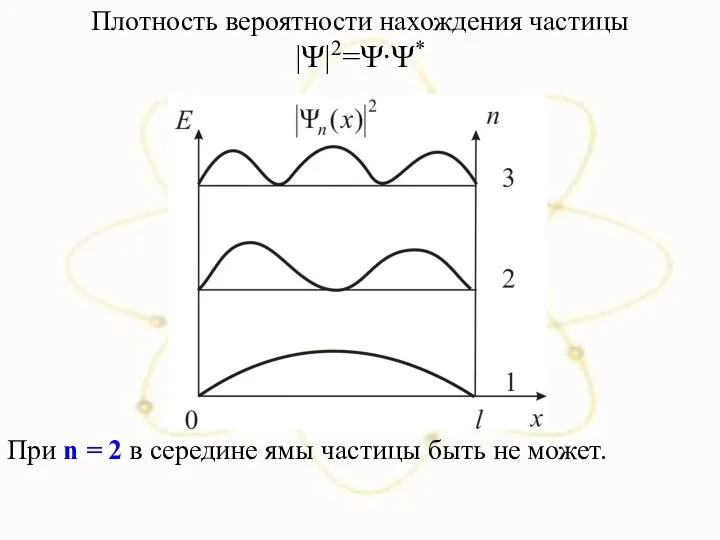
- 27. Плотность вероятности нахождения частицы |Ψ|2=Ψ∙Ψ* При n = 2 в середине ямы частицы быть не может.
- 28. Таким образом, энергия гармонического осциллятора изменяется только порциями, т.е. квантуется Причем минимальная порция энергии Кроме того
- 29. Кроме того, квантово – механический расчет показывает, что частицу можно обнаружить и за пределами ямы, т.е.
- 30. Рассмотрим простейший потенциальный барьер прямоугольной формы высоты U и шириной l для одномерного (по оси х)
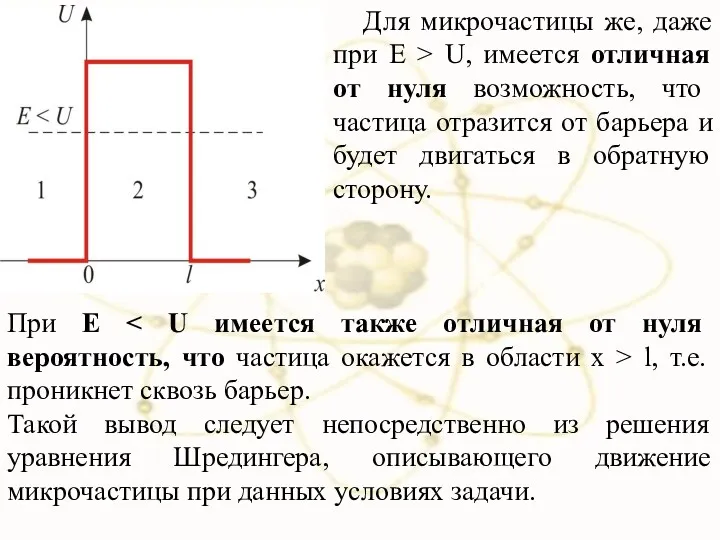
- 31. х При E l, т.е. проникнет сквозь барьер. Такой вывод следует непосредственно из решения уравнения Шредингера,
- 32. Уравнение Шредингера для состояний для каждой их выделенных областей имеет вид: Общее решение этих дифф. уравнений:
- 33. Учитывая значение q и то, что А1 = 1, B3 = 0, получим решение уравнения Шредингера
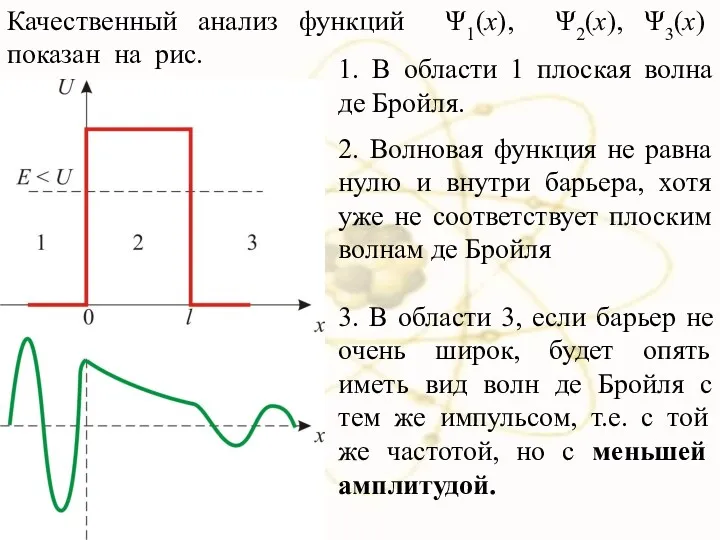
- 34. 1. В области 1 плоская волна де Бройля. 2. Волновая функция не равна нулю и внутри
- 35. Таким образом, квантовая механика приводит к принципиально новому квантовому явлению - туннельному эффекту, в результате которого
- 36. Прохождение частицы сквозь барьер можно пояснить соотношением неопределенностей: Неопределенность импульса на отрезке Δx = l составляет
- 37. С классической точки зрения прохождение частицы сквозь потенциальный барьер при E Туннельный эффект является специфическим квантовым
- 39. Скачать презентацию
























 Момент силы относительно центра
Момент силы относительно центра Условия плавания тел. 7 класс
Условия плавания тел. 7 класс Количество выпускников сдававших ЕГЭ по физике в 2011 г
Количество выпускников сдававших ЕГЭ по физике в 2011 г Динамика материальной точки
Динамика материальной точки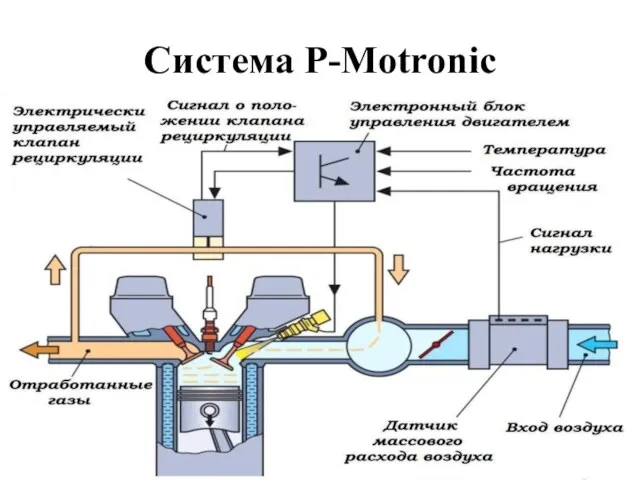 Система P-Motronic
Система P-Motronic Паровая машина
Паровая машина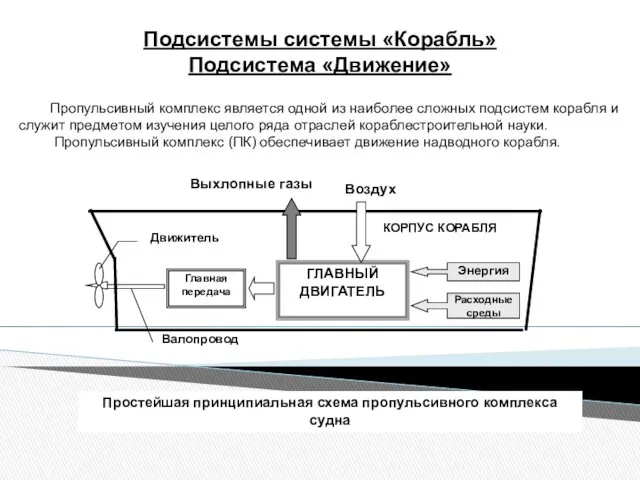 Подсистемы системы Корабль. Подсистема Движение
Подсистемы системы Корабль. Подсистема Движение Научные открытия Ньютона в астрономии
Научные открытия Ньютона в астрономии Авиационный механик (авиационный техник-механик, авиамеханик)
Авиационный механик (авиационный техник-механик, авиамеханик) Ультразвук и инфразвук в природе и технике
Ультразвук и инфразвук в природе и технике Лекция 10. Тема: поляризация
Лекция 10. Тема: поляризация Монтаж заземляющих устройств
Монтаж заземляющих устройств Динамика. Основные понятия
Динамика. Основные понятия Інерція та інертність. Маса та імпульс тіла. Другий закон Ньютона
Інерція та інертність. Маса та імпульс тіла. Другий закон Ньютона От энергии до...
От энергии до... Решение задач. Закон сохранения заряда . Закон Кулона. Напряженность поля точечного заряда
Решение задач. Закон сохранения заряда . Закон Кулона. Напряженность поля точечного заряда Электрическое поле в вакууме
Электрическое поле в вакууме Тепломассообмен
Тепломассообмен Линзы. Оптическая сила линзы
Линзы. Оптическая сила линзы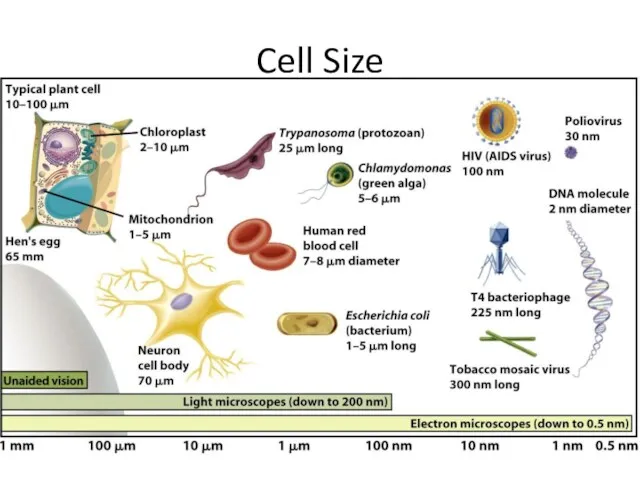 Microscope Measurement
Microscope Measurement Введение в специальность
Введение в специальность Элементы машиноведения
Элементы машиноведения Публичная презентация.
Публичная презентация. Магнитное поле
Магнитное поле Небольшое небесное тело комета
Небольшое небесное тело комета Молекулярная физика и основы термодинамики
Молекулярная физика и основы термодинамики Принцип работы радиотелефонной связи
Принцип работы радиотелефонной связи Атомная физика
Атомная физика