Содержание
- 2. Лектор – Шатохин Константин Станиславович, доцент кафедры Энергоэффективных и Ресурсосберегающих Промышленных Технологий (ЭРПТ), кандидат технических наук
- 3. Рекомендуемая литература: Теплотехника металлургического производства. В 2-х томах. Т. 1. Теоретические основы / Кривандин В.А., Арутюнов
- 4. Тема 1. Гидрогазодинамика Лекция 1
- 5. § 1. Основные понятия механики жидкостей и газов Текучие среды рассматриваются как континуум, или сплошная среда,
- 6. Плотностью среды называется масса вещества, содержащаяся в единице объема, кг/м3: . Если плотность среды постоянна, такая
- 7. В декартовой прямоугольной системе координат вектор скорости можно выразить через его проекции на оси координат: ,
- 8. Идеальной называется жидкость, при движении которой отсутствуют силы внутреннего трения. В противном случае жидкость называется реальной
- 9. Исаак Ньютон установил закон, согласно которому величина τ между двумя слоями прямолинейно движущейся вязкой жидкости пропорциональна
- 10. μ / ρ = ν, м2/с – кинематический коэффициент вязкости, также физический параметр жидкости. Для несжимаемой
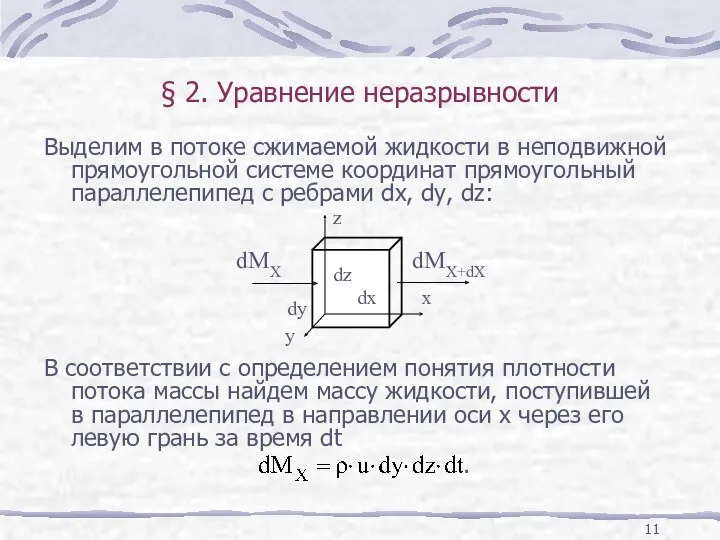
- 11. § 2. Уравнение неразрывности Выделим в потоке сжимаемой жидкости в неподвижной прямоугольной системе координат прямоугольный параллелепипед
- 12. Масса жидкости, вышедшая из параллелепипеда через его правую грань . Разность между массой, поступившей в контрольный
- 13. Разность между массой жидкости, поступившей в параллелепипед, и покинувшей его за время dt, кг: . Приравнивая
- 14. Другая форма записи предыдущего выражения – . Еще одну форму этого уравнения получим, если учтем что
- 15. Окончательно получим . Для случая несжимаемой жидкости, когда плотность постоянна, уравнение неразрывности принимает вид: . В
- 16. Среднее по сечению трубы значение плотности потока массы . Интеграл в правой части – поток массы.
- 17. § 3. Уравнения Эйлера и Навье-Стокса Рассмотрим силы, действующие на выделенный в потоке жидкости контрольный объем
- 18. В направлении оси х на объем действуют силы: 1) внешняя массовая сила dFВН.X = X ⋅
- 19. , где – полная производная, состоящая из локальной и конвективной: . Разделив обе части уравнения на
- 20. Аналогичные уравнения можно получить и для других осей координат: , . Умножив каждое из этих уравнений
- 21. Уравнения Навье-Стокса выведены Анри Навье в 1822 году. Клод Луи Мари Анри Навье (1785–1836) – французский
- 22. Результирующая величина силы внутреннего трения, приложенная к выделенному элементарному объему с учетом направления сил, действующих на
- 23. Подставляя сюда вместо τ его выражение по формуле Ньютона , вынося μ за знак производной и
- 24. Проекция вектора массовой плотности силы внутреннего трения на другие оси: , . Умножив каждую из этих
- 25. Следовательно, уравнение движения реальной несжимаемой жидкости имеет вид: . В случае движения сжимаемой жидкости в уравнении
- 26. При ламинарном режиме частицы движутся по плавным траекториям, все характеристики потока (скорость, давление, температура) – гладкие
- 27. Пульсационно изменяющиеся во времени мгновенные характеристики потока при турбулентном режиме движения называют актуальными значениями этих характеристик.
- 28. Осредненная величина не дает полной информации о структуре турбулентного течения, так как при одном и том
- 29. Для количественной оценки возможности перехода к турбулентному режиму пользуются значением критерия Рейнольдса: Re = o(fИН.) /
- 30. Учтем, что порядок n-ой производной равен отношению порядка функции к порядку аргумента в степени n. Тогда
- 31. Задача расчета движения жидкости заключается в нахождении вектора скорости и давления p как функций координат и
- 32. § 5. Статика жидкостей и газов В неподвижной жидкости отсутствуют силы инерции и трения, то есть
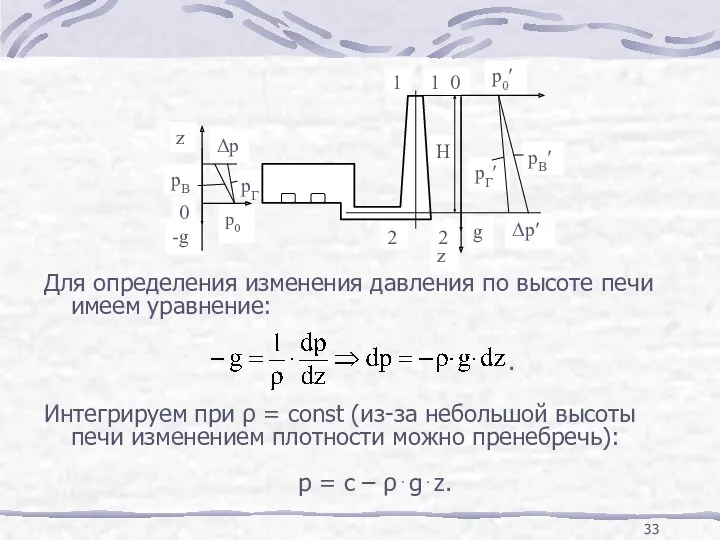
- 33. Для определения изменения давления по высоте печи имеем уравнение: . Интегрируем при ρ = const (из-за
- 34. Полагая z=0, найдем с=p0 – давление на уровне загрузочных окон, поддерживаемое равным давлению в окружающей среде
- 35. Разберем принцип действия дымовой трубы. В сечении 1-1 в устье трубы давление такое же, как в
- 37. Скачать презентацию
































 Двигатели внутреннего сгорания
Двигатели внутреннего сгорания Отделка изделий из металла
Отделка изделий из металла Презентация к уроку развивающего обучения Простые механизмы часть 2
Презентация к уроку развивающего обучения Простые механизмы часть 2 Технология слесарных и слесарно-сборочных работ
Технология слесарных и слесарно-сборочных работ Рост наноструктур и микроскопия. Методы выращивания наноструктур
Рост наноструктур и микроскопия. Методы выращивания наноструктур Динамика кулисного механизма
Динамика кулисного механизма Alternating current. (Lecture 3)
Alternating current. (Lecture 3) Intelligent energy storage
Intelligent energy storage Электростатическое поле в вакууме
Электростатическое поле в вакууме Реальный газ и его работа. (лекция 5в)
Реальный газ и его работа. (лекция 5в) Роботизированная коробка передач DSG
Роботизированная коробка передач DSG Аккумуляторы для крупномасштабного хранения энергии. Лекция 8
Аккумуляторы для крупномасштабного хранения энергии. Лекция 8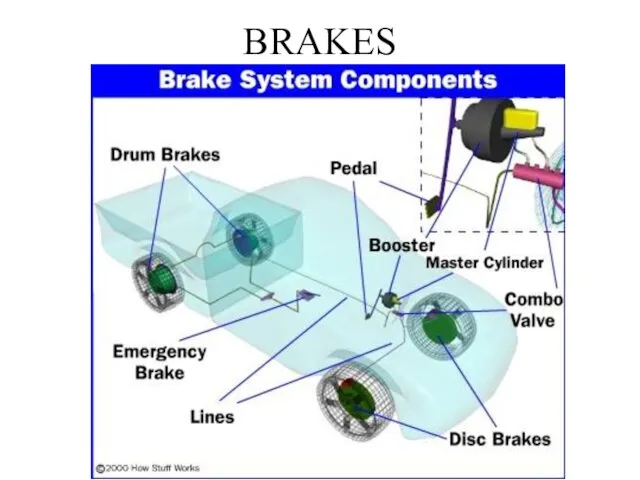 Brakes. Brake System Components
Brakes. Brake System Components разработка технологического процесса на механическую обработку детали фланец
разработка технологического процесса на механическую обработку детали фланец Подшипники. Смазочные материалы
Подшипники. Смазочные материалы Как можно обрабатывать заготовки из древесины, имеющие цилиндрическую форму. Устройство токарного станка по дереву
Как можно обрабатывать заготовки из древесины, имеющие цилиндрическую форму. Устройство токарного станка по дереву Всероссийский турнир юных физиков. Катание на диске
Всероссийский турнир юных физиков. Катание на диске Макросистема (термодинамическая система)
Макросистема (термодинамическая система)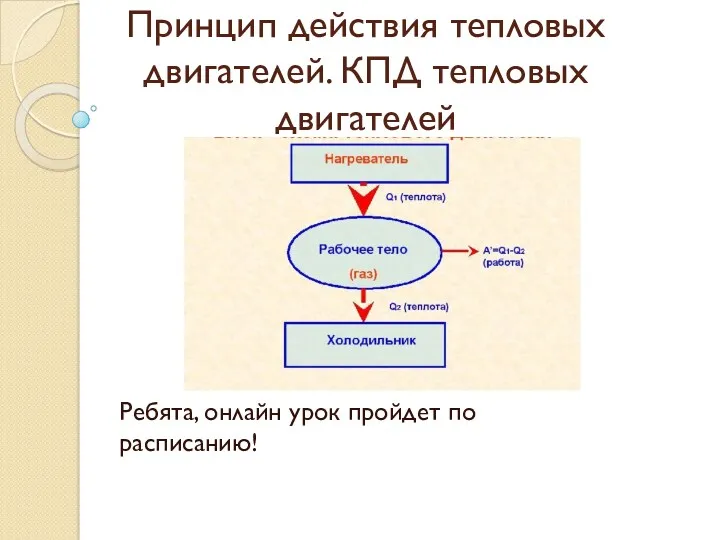 Принцип действия тепловых двигателей. КПД тепловых двигателей
Принцип действия тепловых двигателей. КПД тепловых двигателей Притяжение Земли
Притяжение Земли Шкала электромагнитных волн.
Шкала электромагнитных волн. Теории прочности
Теории прочности Виды эксплуатационных разрушений и причины их возникновения
Виды эксплуатационных разрушений и причины их возникновения Электрический ток в электролитах
Электрический ток в электролитах Урок с презентацией Рентгеновские лучи
Урок с презентацией Рентгеновские лучи Спектроскопические методы анализа. Методы атомной и молекулярной спектроскопии
Спектроскопические методы анализа. Методы атомной и молекулярной спектроскопии Проект урока по теме Звуковые волны 9 класс
Проект урока по теме Звуковые волны 9 класс Решение нестандартных задач по физике
Решение нестандартных задач по физике